ZOJ ~ 3593 ~ One Person Game （扩展欧几里得，不定方程）

最新推荐文章于 2020-07-22 18:33:43 发布

张松超

最新推荐文章于 2020-07-22 18:33:43 发布

阅读量362

点赞数 1

CC 4.0 BY-SA版权

分类专栏：【素数/同余/不定方程/乘性函数】

本文链接：https://blog.youkuaiyun.com/ZscDst/article/details/82917139

【素数/同余/不定方程/乘性函数】专栏收录该内容

10 篇文章

订阅专栏

本文深入探讨了一种算法，用于解决从点A到点B的最短步数问题，其中每步可以选择a步、b步或a+b步。通过扩展欧几里得算法求解线性方程组，找到可能的最小步数方案。文章详细解释了如何通过调整步数比例，寻找最优解，并提供了完整的C++代码实现。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

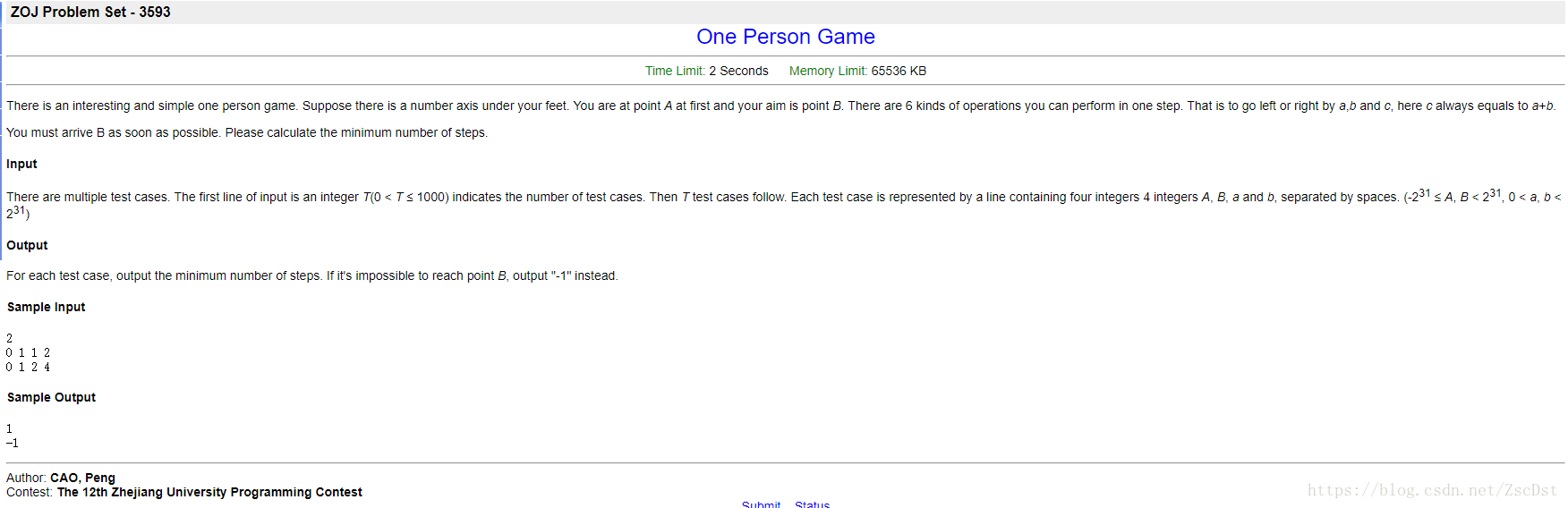
题意

你要从A走到B，你每次可以走a步，b步，a+b步问最小需要走多少步？无法到达输出 -1。

题解

先不考虑a+b步的情况，那么我们要求解的就是： $ax+by=|A-B|$ ，如果 $|A-B|\%gcd(a,b) != 0$ ，证明无解。

假设原方程一组解为x0，y0，那么通解(x，y)为： $& (x0+b'*t,\quad y0-a'*t)$ ， $a'=a/gcd,\quad b'=b/gcd$ 。
其实也就是两条直线： $x = b't+x0$ ， $y = -a't+y0$

取一条平行于y轴的直线 x = t ：

如果 x 和 y 异号，假设x > 0,y < 0也就是往前走x次a步，往后走y次b步。x < 0, y > 0同理，这种情况答案为 $|x| + |y|$

如果 x 和 y 同号，其实也就是都往前(后)走x次a步，y次b步，考虑上可以走a+b的情况，答案也就是 $max(|x| , |y|)$ 。

结合图可知，越接近交点值越小，当 t 取 x 和 y 交点时，答案最小。

$a't+x0=-b't+y0$ =》 $t = (y0-x0)/(a'+b')$ ，但是 t 可能不是整数，所以我们要尝试 t-1，t，t+1 三个值。

#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
void exgcd(LL a, LL b, LL& d, LL& x, LL& y)
{
    if (!b) { d=a; x=1; y=0; }
    else { exgcd(b, a%b, d, y, x); y -= x*(a/b); }
}
LL cal(LL x, LL y)
{
    if (x*y >= 0) return max(abs(x), abs(y));
    else return abs(x)+abs(y);
}
LL solve(LL a, LL b, LL c)
{
    LL GCD, x0, y0;
    exgcd(a, b, GCD, x0, y0);
    if (c%GCD) return -1;
    x0 *= c/GCD; y0 *= c/GCD;

    LL aa = a/GCD, bb = b/GCD;
    LL t = (y0-x0)/(aa+bb);//x0+a't=y0-b't，t = (y0-x0)/(a'+b')
    LL ans1 = cal(x0+bb*t, y0-aa*t);
    LL ans2 = cal(x0+bb*(t-1), y0-aa*(t-1));
    LL ans3 = cal(x0+bb*(t+1), y0-aa*(t+1));
    return min(min(ans1, ans2), ans3);
}
int main()
{
    int T; scanf("%d", &T);
    while (T--)
    {
        LL A, B, a, b; scanf("%lld%lld%lld%lld", &A, &B, &a, &b);
        LL ans = solve(a, b, abs(A-B));
        printf("%lld\n", ans);
    }
    return 0;
}
/*
2
0 1 1 2
0 1 2 4
*/