494. 目标和/C++

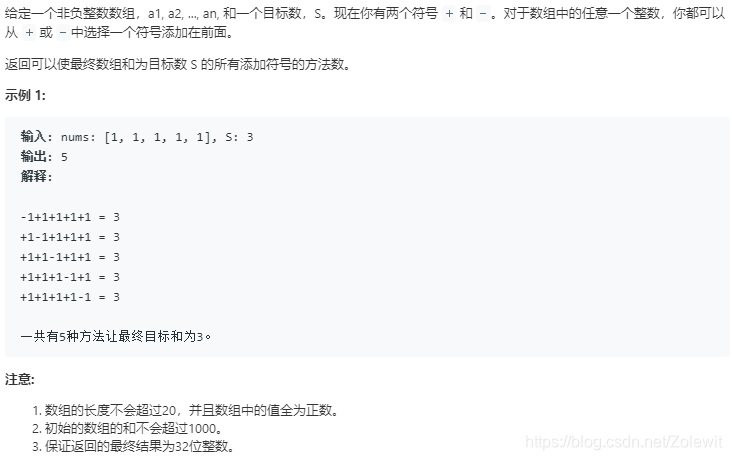
将数字分为两个部分，加正号的数字的和为positiveSum，加负号的数字的和为negativeSum，
则有positiveSum-negativeSum=S
又因为positiveSum+negativeSum=sum
则positiveSum=(S+sum)/2

由此，问题转化为从nums中挑若干数字，令其和为positiveSum。实质是01背包问题。
dp[i]就是选取的数字和为i的方法数。

int findTargetSumWays(vector<int>& nums, int S) {
    int sum = accumulate(nums.begin(),nums.end(),0);
    if(sum < S || (sum+S)&1) return 0;
    
    int positiveSum = (sum+S)/2;
    vector<int> dp(positiveSum+1);
    dp[0]=1;
    for(int num:nums)
        for(int i=positiveSum;i>=num;--i)//如果背包容量i比num小，则退出for循环
            dp[i]+=dp[i-num];//dp[i]=dp[i]+dp[i-num]，即是不选num的方法数+选num的方法数
    return dp[positiveSum];
}