day14 代码随想录 | 对称二叉树 二叉树最大深度 二叉树最小深度

关于这个三个leetcode，都可以用递归和迭代的思想去处理。但对于二叉树，优先使用递归更加能体现抽象的过程，还是说的是递归三部曲

101 对称二叉树

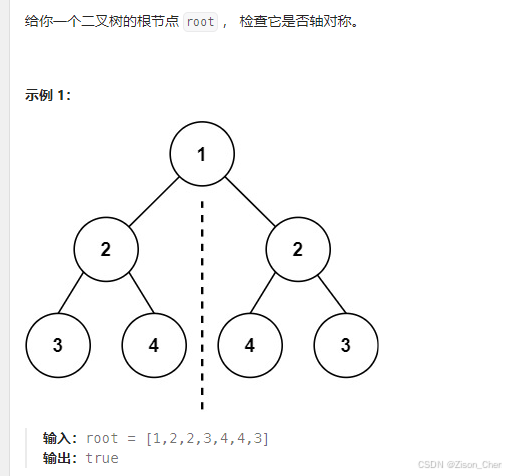
这个题目看着挺简单，但是有很多细节需要注意

递归法

对于二叉树的递归，需要明确采用那种遍历方式。前中后，用哪一种？

对称二叉树，我们需要比较左子树的外侧和右子树的外侧，左子树的内测和右子树的内测是否相等。遍历只能是后续，左子树 是 左右中 右子树是右左中，然后比较是否相等。

有了这个思路，递归就好写了。

1. 确认递归的参数和返回值。 参数就是左右子树，返回就是判断是否相等

2. 中止条件。当不对称的时候，就可以中止了

   - 左边或者右边 一边为空 一边不为空  false

   - 左边和右边都为空 返回true

   - 左边和右边都不为空 比较值是否相等

3. 单层递归

    后序遍历 + 比较

def isSymmetric(root):
    def dfs(leftNode, rightNode):
        if (leftNode == None and rightNode != None): return False
        elif (leftNode != None and rightNode == None): return False
        elif (leftNode == None and rightNode == None): return True
        elif (leftNode.val != rightNode.val): return False

        # 能进入到这里 说明 leftNode.val == rightNode.val 需进入下一层继续判断
        # 后续遍历
        left = dfs(leftNode.left, rightNode.right) # 左子树 左 右子树 右
        right = dfs(leftNode.right, rightNode.left) # 左子树 右 右子树 左
        isSame = left and right # 左子树 中 右子树 中
        
        return isSame
    if not root:
        return True

    return dfs(root.left, root.right)
    

    迭代法

迭代法其实就可以用采用队列或者栈，在加入的顺序上做操作。

def isSymmetric(root: node):
    if not root:
        return True
    from collections import deque
    queue = deque()
    queue.append(root.left)
    queue.append(root.right)

    while queue:
        left = queue.popleft()
        right = queue.popleft()

        if not left and not right:
            continue
        
        if not left or not right or left.val != right.val:
            return False
        
        queue.append(left.left)
        queue.append(right.right)
        queue.append(left.right)
        queue.append(right.left)

    return True

二叉树最大深度

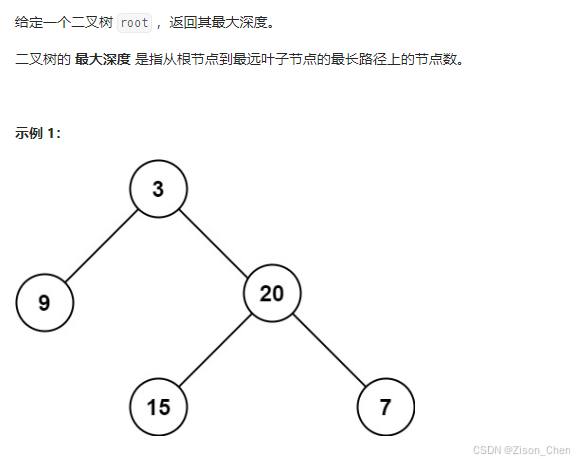
这是二叉树的最大深度，其实就是二叉树的高度，可以用后序遍历来完成 左右中

也可以用层次遍历

递归 后序遍历

我们遍历左子树 和右子树 然后取其中的最大再加上 根节点的高度1

递归三部曲：

1. 确认递归函数的参数和返回值。返回的是深度，参数就是节点

2. 递归函数的中止条件。当遇到空节点，就返回。

3. 单层递归

    如果遇到空 返回0

    然后访问左子树 得到左子树的深度

    访问右子树 得到右子树的深度

    最后 取最大 

def maxDepth(root):
    def getDepth(node):
        if not node:
            return 0
        leftDepth = getDepth(node.left) # 左
        rightDepth = getDepth(node.right) # 右
        depth = 1 + max(leftDepth, rightDepth) # 中
        
        return depth

    return getDepth(root)

层次遍历

def maxDepth(root):
    if not root:
        return 0
    from collections import deque
    queue = deque([root])
    
    depth = 0
    while queue:
        depth += 1
        for _ in range(len(queue):
            node = queue.popleft()

            if node.left:
                queue.append(node.left)
            if node.right:
                queue.append(node.right)

    return depth

二叉树最小深度

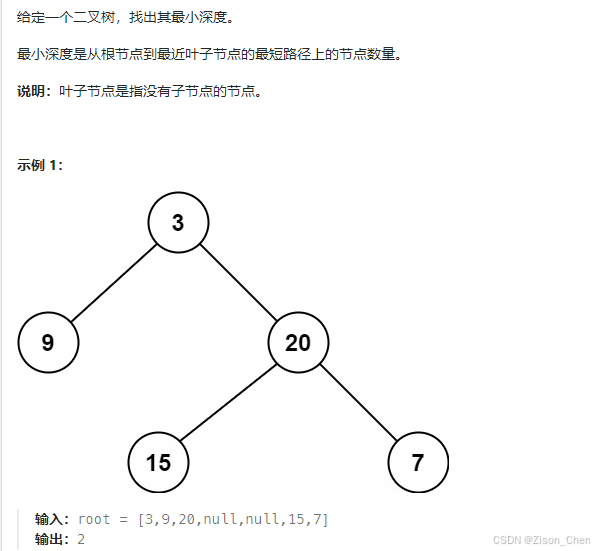
看似与最大深度差不多，好像只需要将max改为min就可以了，但是这是不对的。如下图，直接改的话会，会返回深度为1.

最小深度是从根节点到最近叶子节点的最短路径上的节点数量。注意是叶子节点.

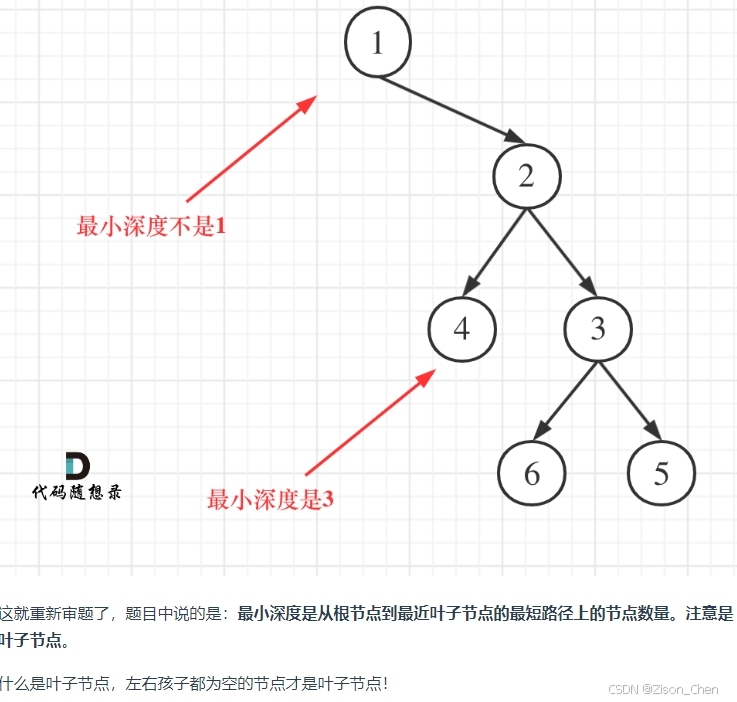
那么，我们如何改动呢。其实，很简单，那就是如果判断左右子树是否为空。如果为空，

那么我们就＋右子树的深度，反之，则加左子树。

递归 后序遍历

def minDepth(root:node):
    def getDepth(node):
        if not node:
            return 0
        leftDepth = getDepth(node.left)
        rightDepth = getDepth(node.right)
        
        if node.left == None and node.right != None:
            return 1 + rightDepth

        if node.right == None and node.left != None:
            return 1 + leftDepth

        depth = 1 + min(leftDepth, rightDepth)
        return depth
    
    return getDepth(root)

层序遍历

层序遍历需要做的修改就是，但是左子树和右子树都为空（说明是叶子节点），返回depth

def minDepth(root: node):
    if not root:
        return 0
    from collections import deque
    
    queue = deque([root])
    
    depth = 0
    
    while queue:
        depth += 1
        for _ in range(len(queue)):
            node = queue.popleft()
            
            if not node.left and not node.right:
                return depth

            if node.left:
                node.append(node.left)
            
            if node.right:
                node.append(node.right)

    return depth

图片来源：leetcode， 代码随想录