算法练习day12——190331（并查集）

1.并查集

1.1 简介

• 用于解决检查两个元素是否属于一个集合；
• 合并两个元素各自所在的集合；

即：

• isSameSet(A,B)：其中A属于set1，B属于set2，看set1和set2是否为同一个集合。
• unionSet(A,B)：将A所在的集合set1和B所在的集合set2全部合并在一起，组成一个大集合set。使得set1中的任何一个元素肯定和set2中的任何元素在同一个集合中。

注：并查集初始化时必须把所有元素给出。

实现上述两个功能可以用任意结构，比如：

• list：
  • 通过A得到set1，然后遍历set1看有没有B
  • 将两个链表接起来
• set：
  • 看set1中是否有B，O(1)
  • 将set2中的数据重新哈希，然后放到set1中，这得遍历。

向上指针指向自己说明是这个集合的代表节点；

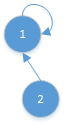
将2节点挂在1节点的后面。

若要找2节点的代表节点，则顺着2节点的向上指针往上找，找到一个节点的向上指针指向自己，此节点就是代表节点。

并查集是一棵多叉树：

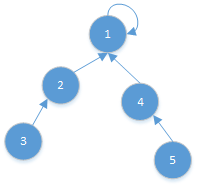
是否在同一个集合：A、B各自向上找自己的代表节点，看是否相同。

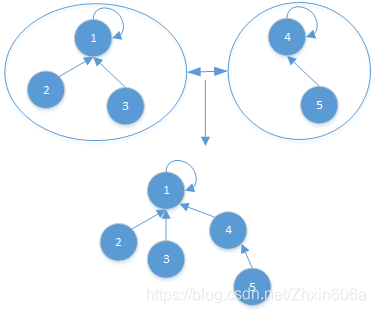
合并：节点少的挂在节点多的集合的代表节点下。

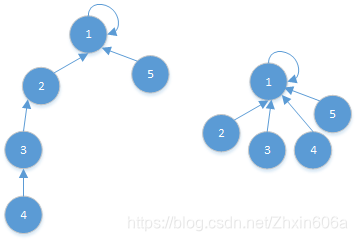
优化：在查找4的代表节点时，找到1后，将4-1这条路径经过的节点变为扁平的（将图左边的结构变为右边的结构），都直接连在代表节点1上。4之后的节点先不管。

fatherMap：<child,father>，存的是节点和它的父亲，依据这个表可以找到节点的所在集合的代表节点。

sizeMap：<node,Integer>，某一个节点它对应的集合中的节点个数。

1.2 代码实现

import java.util.HashMap;
import java.util.List;

public class UnionFind {

	public static class Node {
		// whatever you like
	}

	public static class UnionFindSet {
		public HashMap<Node, Node> fatherMap;//<child,father>
		public HashMap<Node, Integer> sizeMap;

		public UnionFindSet(List<Node> nodes) {
			makeSets(nodes)
		}

		private void makeSets(List<Node> nodes) {
			fatherMap = new HashMap<Node, Node>();
			sizeMap = new HashMap<Node, Integer>();
			for (Node node : nodes) {
				fatherMap.put(node, node);//链表中每个节点是一个独立的集合，指向自己
				sizeMap.put(node, 1);//集合中的节点数为1
			}
		}

		private Node findHead(Node node) {//找某个节点所在集合的代表节点
			Node father = fatherMap.get(node);
			//递归
			if (father != node) {
				father = findHead(father);
			}
			fatherMap.put(node, father);//扁平化
			return father;
		}
		
		public boolean isSameSet(Node a, Node b) {
			return findHead(a) == findHead(b);
		}

		public void union(Node a, Node b) {
			if (a == null || b == null) {
				return;
			}
			Node aHead = findHead(a);
			Node bHead = findHead(b);
			if (aHead != bHead) {
                            //不在一个集合中才需要合并
				int aSetSize= sizeMap.get(aHead);
				int bSetSize = sizeMap.get(bHead);
				if (aSetSize <= bSetSize) {
                                        //a中元素个数少，则将a的father指向b
					fatherMap.put(aHead, bHead);
					sizeMap.put(bHead, aSetSize + bSetSize);//只改了代表节点的size，其他节点的不用管
                                        //只有head的size是有用的信息，其他节点的size用不到
				} else {
					fatherMap.put(bHead, aHead);
					sizeMap.put(aHead, aSetSize + bSetSize);
				}
			}
		}
	}
}

查两个元素是否在一个集合，也可任意决定两个集合是否合并。——只要两个操作的总次数逼近O(N)及以上，那么平均下来，单次查询和合并的时间复杂度为O(1)。

findHead()的详细过程，假设当前node为节点4：

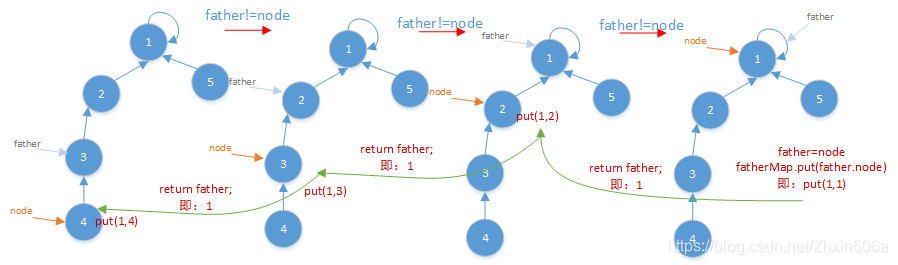
最终结果：

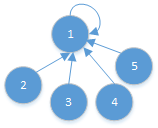
findHead()的非递归实现：

public node findHead(Node node){
    Node cur=node;
    Node father=fatherMap.get(cur);
    Stack<Node> stack=new Stack<Node>();
    
    while(cur!=father){
        stack.put(cur);
        cur=father;
        father=fatherMap.get(father);
    }
    while(!stack.isEmpty()){
        fatherMap.put(stack.pop(),father);
    }
    return father;
}

1.3 举例

岛问题

一个矩阵中只有0和1两种值， 每个位置都可以和自己的上、 下、 左、 右四个位置相连， 如果有一片1连在一起， 这个部分叫做一个岛， 求一个矩阵中有多少个岛？

举例：

0 0 1 0 1 0
1 1 1 0 1 0
1 0 0 1 0 0
0 0 0 0 0 0

这个矩阵中有三个岛。

1.3.1 分析

这个问题原问题不用并查集结构，可用递归结构搞定。

但是若给定的矩阵特别大，需采用分治思想，多任务并行。

具体方法：

给定如下矩阵：

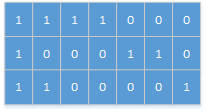
使用双层for循环，遍历每一个位置的元素，当遍历到某个位置时：

• 若此位置的元素为1时，将其相连的1都变为2，岛数量加1——感染；
• 若为0，跳过；
• 若为2，也跳过.

上述矩阵，当遍历到(0,0)位置时，元素为1，则感染结果如下图：

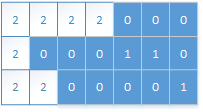
岛数量由0变为1；

后面一直是2或0，直接跳过，直到位置(1,4)时，是1，则感染，岛数量变为2：

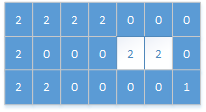
再直到遍历到最后一个位置的元素时，才是1，感染为2，岛数量加一，变为3：

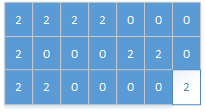
所以岛数量为3.

1.3.2 代码实现

package Hash;

public class IslandCount {
	public static void main(String[] args) {
		int[][] m1 = {  { 0, 0, 0, 0, 0, 0, 0, 0, 0 }, 
				        { 0, 1, 1, 1, 0, 1, 1, 1, 0 }, 
				        { 0, 1, 1, 1, 0, 0, 0, 1, 0 },
				        { 0, 1, 1, 0, 0, 0, 0, 0, 0 }, 
				        { 0, 0, 0, 0, 0, 1, 1, 0, 0 }, 
				        { 0, 0, 0, 0, 1, 1, 1, 0, 0 },
				        { 0, 0, 0, 0, 0, 0, 0, 0, 0 }, };
		System.out.println(islandCount(m1));

		int[][] m2 = {  { 0, 0, 0, 0, 0, 0, 0, 0, 0 }, 
						{ 0, 1, 1, 1, 1, 1, 1, 1, 0 }, 
						{ 0, 1, 1, 1, 0, 0, 0, 1, 0 },
						{ 0, 1, 1, 0, 0, 0, 1, 1, 0 }, 
						{ 0, 0, 0, 0, 0, 1, 1, 0, 0 }, 
						{ 0, 0, 0, 0, 1, 1, 1, 0, 0 },
						{ 0, 0, 0, 0, 0, 0, 0, 0, 0 }, };
		System.out.println(islandCount(m2));

	}
	public static int islandCount(int[][] arr) {
		int N=arr.length;
		int M=arr[0].length;
		int count=0;
		
		for(int i=0;i<N;i++) {
			for(int j=0;j<M;j++) {
				if(arr[i][j]==1) {
					count++;
					infect(arr,i,j,N,M);
				}
			}
		}
		return count;
	}
	
	public static void infect(int[][] arr,int i,int j, int N,int M) {
		if(i<0||i>N||j<0||j>M||arr[i][j]!=1)
			return;
		arr[i][j]=2;
		infect(arr,i+1,j,N,M);//右
		infect(arr,i,j+1,N,M);//下
		infect(arr,i-1,j,N,M);//左
		infect(arr,i,j-1,N,M);//上
	}
}

运行结果：

分割，让多CPU运行，然后用合适的合并逻辑进行合并。

• 合并时需要处理边界信息，如下图：

左有3个岛，右有2个岛，但是合起来之后只有4个岛。

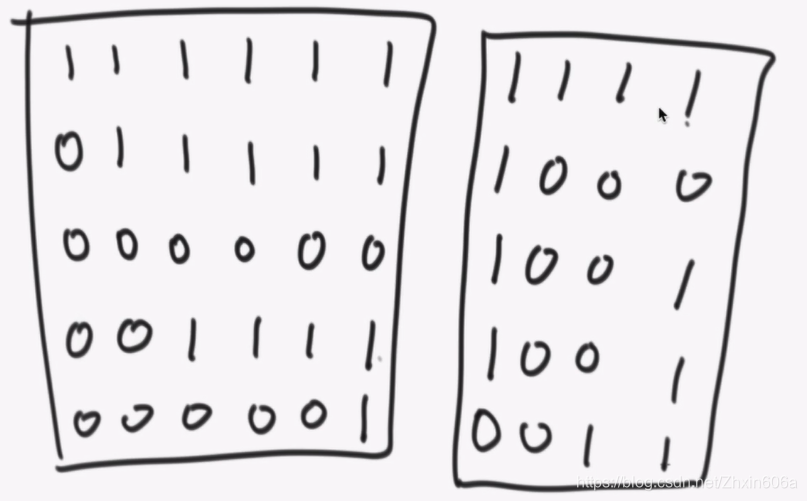
确定每个感染点的感染中心，如下：

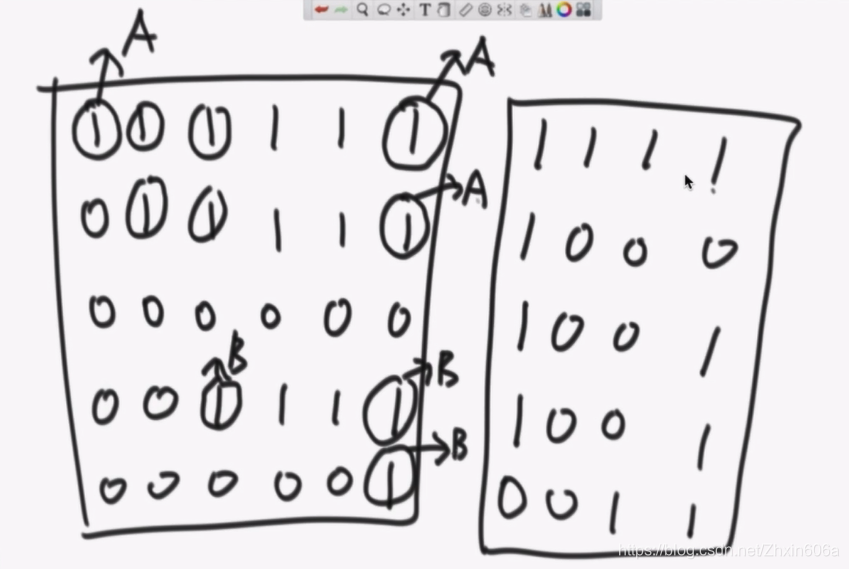
左边矩阵中有A和B两个感染中心。需要记录的信息：

• 岛的个数是两个
• 边界中4个1的感染中心分别是什么。
• 右边矩阵的分析如下：

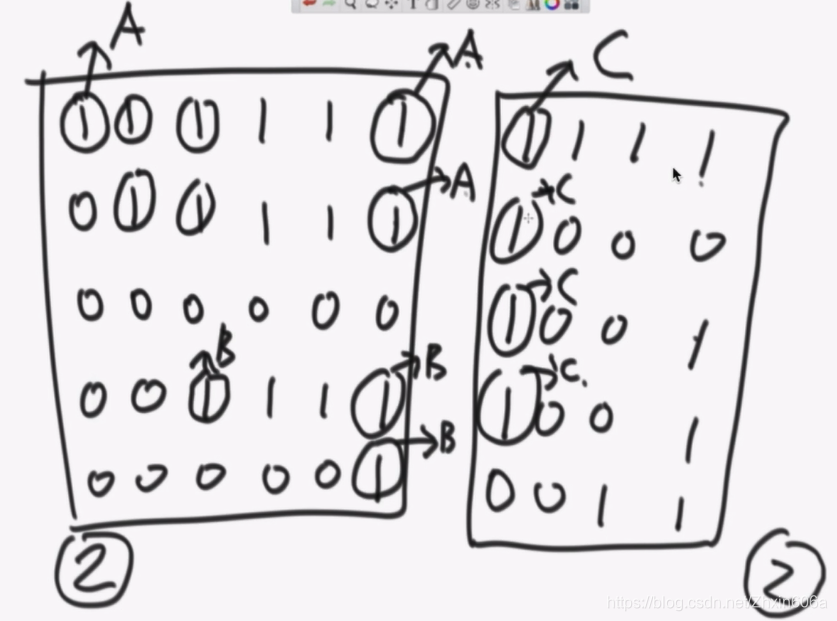
合并的时候：

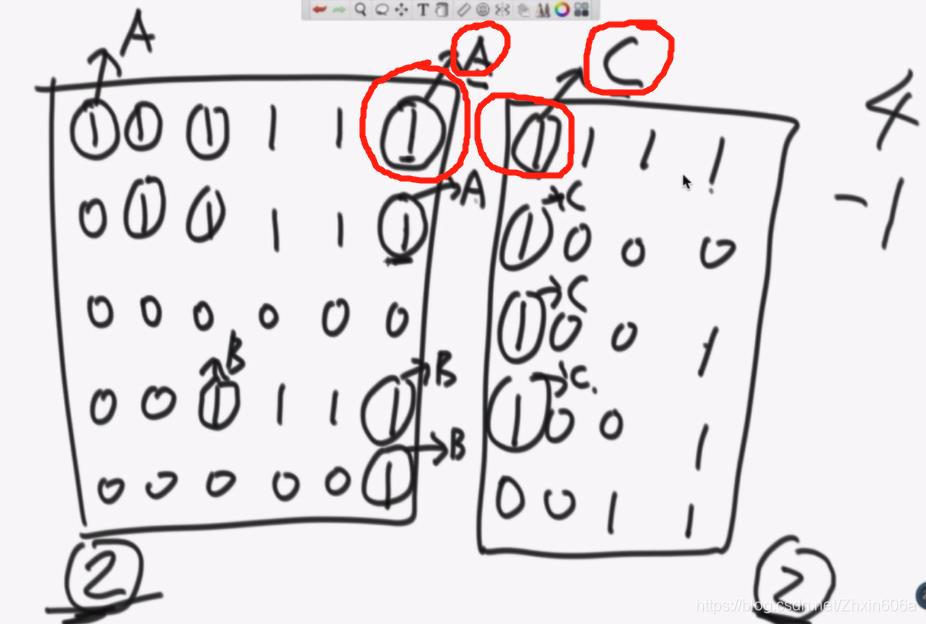
• 先看这两个1的感染中心点A和C是否在一个集合中，不在，说明没有合并过，岛的总个数-1，然后将A和C合在一起；
• 接着下一对，感染中心还是A，C，已经在一个集合中了，不管；
• 下面是B和C，不在一个集合中，则岛的总个数-1，将B和C放在一个集合中。

可将左右的边界信息放在一个分布式内存中，即在这个分布式内存中维护一个并查集，这个可用spark做。