【数据结构】归并排序（递归+非递归）

---

1. 概念

归并：将两个或两个以上的有序表组合成一个新有序表。
归并的条件：每个序列都是有序的。
归并排序的过程：将n个数据看成n个有序的序列，每个序列长度为1。两两有序序列归并，合成长度为2的有序序列。不断归并，最终剩下长度为n的有序序列。

---

2. 画图

---

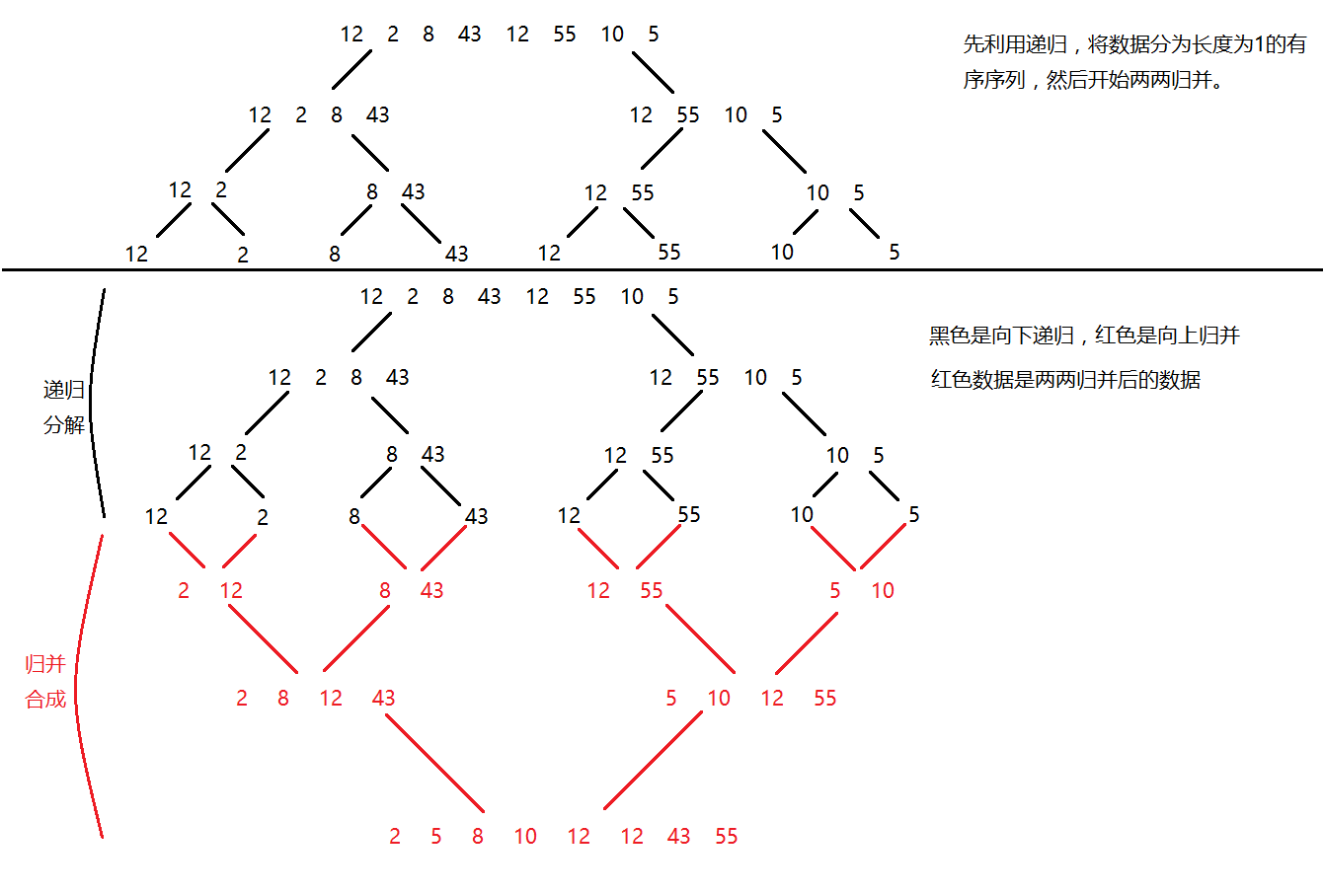
3. 代码实现

void _MergeSort(int* a, int begin, int end, int* tmp)
{
	if (begin >= end)
	{
		return;
	}
	int mid = (begin + end) / 2;
	//[begin , mid][mid+1 , end]
	_MergeSort(a, begin, mid,tmp);
	_MergeSort(a, mid + 1, end, tmp);
	//进行归并
	int begin1 = begin, end1 = mid;
	int begin2 = mid + 1, end2 = end;
	int i = begin;//放在临时空间对应的位置
	while (begin1 <= end1 && begin2 <= end2)
	{
		if (a[begin1] > a[begin2])
		{
			tmp[i++] = a[begin2++];
		}
		else
		{
			tmp[i++] = a[begin1++];
		}
	}
	//将剩余的元素直接插入临时空间
	while (begin1 <= end1)
	{
		tmp[i++] = a[begin1++];
	}
	while (begin2 <= end2)
	{
		tmp[i++] = a[begin2++];
	}
	//将排序完的数据拷贝会数组
	memcpy(a + begin, tmp + begin, sizeof(int) * (end - begin + 1));
}
void MergeSort(int* a, int n)
{
	int* tmp = (int*)malloc(sizeof(int) * n);//用来存储归并后的临时数据
	if (tmp == NULL)
	{
		perror("malloc failed");
		return;
	}
	_MergeSort(a, 0, n - 1, tmp);//归并需要递归，需另写一个函数来实现，否则tmp会多次申请空间
	free(tmp);
}

算法分析
时间复杂度
最坏情况下，递归的层次是接近logN层，每层需要比较排序N次，所以时间复杂度是O（NlogN）。
空间复杂度
需要额外开辟一个tmp来存储临时数据，时间复杂度是O（N）。
稳定性
第一组数据在前面，第二组数据在后面，当第一组数据的元素和第二组数据的元素相等时，将第一组数据导入临时数组，所以是稳定的。

---

4. 非递归实现

1. 思想
   先两两归并长度为1的有序序列，此时得到长度为2的有序序列，再两两归并得到长度为4的有序序列，以此类推，最终得到长度为n的有序序列。但如果出现长度为奇数的序列怎么办？
   

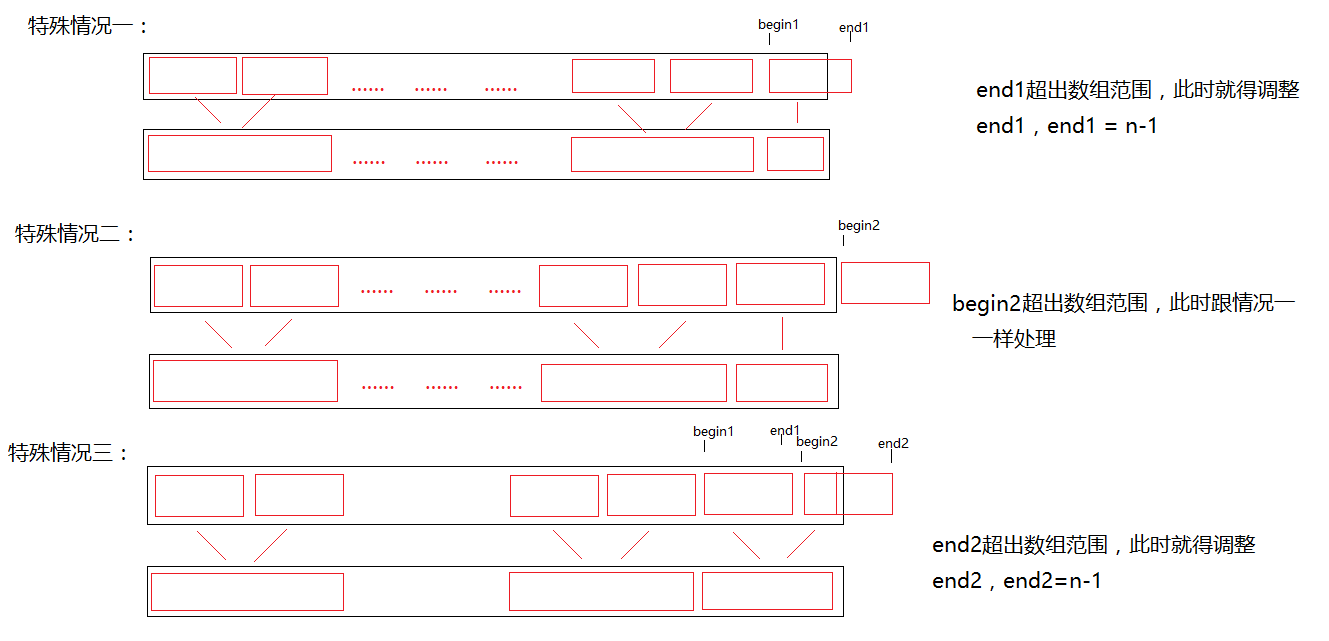
2. 代码实现

//非递归归并排序
void MergeSortNonR(int* a, int n)
{
	int* tmp = (int*)malloc(sizeof(int) * n);//用来临时存放数据
	if (NULL == tmp)
	{
		perror("malloc fail");
		return;
	}
	int gap = 1;
	while (gap < n)//每组的个数不能超过n个
	{
		for (int i = 0; i < n; i += 2*gap)//每次都是两组比较
		{
			int begin1 = i, end1 = i + gap - 1;
			int begin2 = i + gap, end2 = i + 2 * gap - 1;
			if (end1 >= n)//特殊情况1
			{
				end1 = n - 1;
				begin2 = n + 1;//修正后的第二组的区间不存在，所以不进行循环
				end2 = n;
			}
			else if (begin2 >= n)//特殊情况2
			{
				begin2 = n;//第一组没越界，第二组越界了。将第一组拷贝下去，第二组区间设置不存在
				end2 = n - 1;
			}
			else if (end2 >= n)//特殊情况3
			{
				end2 = n - 1;//此时第二组的数据有部分在数组范围内，所以调整end2即可
			}
			//进行归并
			int j = 0;
			while (begin1 <= end1 && begin2 <= end2)
			{
				if (a[begin1] > a[begin2])
				{
					tmp[j++] = a[begin2++];
				}
				else
				{
					tmp[j++]  = a[begin1++];
				}
			}
			while (begin1 <= end1)
			{
				tmp[j++] = a[begin1++];
			}
			while (begin2 <= end2)
			{
				tmp[j++] = a[begin2++];
			}
			memcpy(a + i, tmp, sizeof(int) * (end2 - i + 1));
		}
		gap *= 2;
	}
	free(tmp);
}