树状数组总结

树状数组

一、Lowbit

1. 说明

$lowbit$ 操作即为去当前数 2 进制中的最后一位 1 及其后面的 0 的十进制值；

2. 求法

求法1

思路

由于求最后一位 1 及可想到将原数 - 1;

$x$ 的二进制可以看做 A1B (A是最后一个 1 之前的部分，B是最后一个1之后的0 )，$i-1$ 的二进制可以看做 A0C (C和B一样长)，所以 $i\&(i-1)$ 的二进制就是 A1B & A0C = A0B ；

即此时再用 $i$ 减去此值即可得到 A1B – A0B = 0…010…0 ；

方法

对于十进制数 $x$ ，可先将原数转化成二进制之后的最后一位 1 替换成 0，即减去1，然后再用原数十进制减去替换掉最后一位 1 后的十进制数 ，答案就是 $lowbit(x)$ 的结果；

int lowbit(int x) { return x - (x & (x - 1)); }

求法2

思路

设 $x>0$ ，$x$ 的第 $k$ 位为 1 ，则后第 $1\sim k-1$ 位均为 0 ；

则先将 $x$ 取反，使 $k$ 位变为 0 ，则后第 $1\sim k-1$ 位均为 1 ；

再将 $x+1$ ，此时由于进位， $x$ 的第 $k$ 位变为 1 ，则后第 $1\sim k-1$ 位都是 0 ；

则 $x$ 此时的前 $1\sim k-1$ 与原 $x$ 相反，所以 $x\&(\sim x+1)$ 仅有第 $k$ 位为 1 ；

又由于补码表示下 $\sim x=-1-x$

所以 $lowbit(x)=x\&(\sim x+1)=x\&(-x)$ ；

求法

int lowbit(int x) { return x & (-x); }

二、树状数组

1. 引入

对于数组内的单点修改及区间查询，若用普通数组，修改十分快速，但区间查询需要一个一个元素的加；若用前缀和元素，虽然查询区间和十分快速，但修改元素又十分困难；

其基本原因为普通数组每个元素维护的区间包含的元素个数太少，而前缀和数组又太多；

所以，可以用一个数组 $BIT$ 维护若干个小区间，在单点修改时，只更新包含这一元素的区间，区间查询时只对包含区间内元素的区间进行组合，得到区间和；

树状数组 (Binary Index Tree, B.I.T) 即为这样的数据结构；

2. 定义

树状数组利用了 2 进制分解定理，即任意一个数都可以由若干个 2 的幂表示；

则可将原数组分为 $lo{g}_2(n)$ 个长度为 2 的幂的区间，分别对其进行区间内所有元素和的维护，如下图所示；

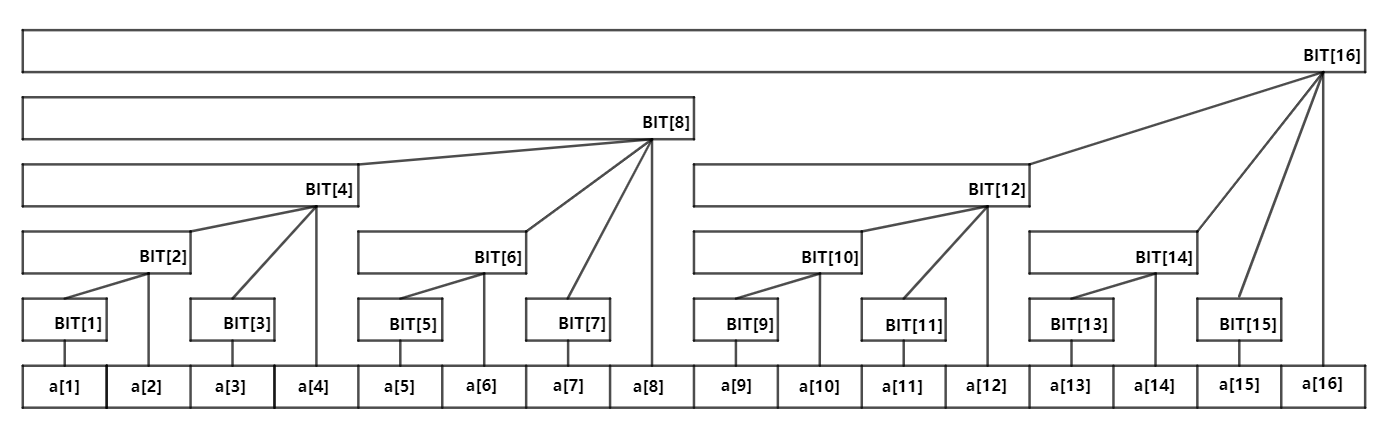
树状数组即为一种可在 $Olo{g}_2(n)$ 时间复杂度内对原数组进行区间，单点的修改，查询的数据结构；

3. 性质

则树状数组 $BIT$ 的特点为，

1. $BIT[i]$ 维护 $(i-lowbit(i),i]$ 的区间和；
2. 对于每个节点 $BIT[i]$ 的子结点个数为 $lowbit(i)$ 的值；
3. 除树根外，每个内部节点 $BIT[i]$ 的父节点为 $c[i+lowbit(i)]$ ；
4. 树的深度为 $lo{g}_2(n)$ ；

三、基本操作

1. 单点修改，区间查询

单点修改

设将 $x$ 加上 $a$ ；

则 $BIT[x]$ 及其祖先节点维护了 $a[x]$ 的值，又由于树状数组中除树根外，每个内部节点 $BIT[x]$ 的父节点为 $c[x+lowbit(x)]$ ，可通过将 $x$ 每次增加 $lowbit(x)$ 直到 $n$ 得到要修改的树状数组区间，每个区间和 + a 即可；

void add(int x, int a) {
	while (x <= n) {
		BIT[x] += a;
		x += lowbit(x);
	}
	return;
}

初始化

一般的树状数组初始化时即建立一个空的树状数组，在对于数组的数 $a[i]$ 通过 add(i, a[i]) 单点修改加入树状数组，时间复杂度为 $O(nlo{g}_2(n))$ ；

但由于$BIT[i]$ 维护 $(i-lowbit(i),i]$ 的区间和，所以可在输入时预处理数组前缀和，再通过 BIT[i] = sum[i] - sum[i - lowbit(i)] 初始化树状数组，时间复杂度为 $O(n)$ ；

void firstset(int n) {
	for (int i = 1; i <= n; i++) {
		BIT[i] = sum[i] - sum[i - lowbit(i)];
	}
	return;
}

区间查询

设查询 $[l,r]$ 的区间和为例；

则由于线段树原维护的为从 2 的幂为起点的区间和，所以可以类似前缀和先求出 $[1,r]$ 的区间和，再减去 $[1,l-1]$ 的区间和；

可类比单点修改操作计算 $[1,x]$ 的和；

由于 $BIT[x]$ 及其儿子节点维护了 $[1,x]$ 的值，又由于树状数组中除树根外，每个内部节点 $BIT[x]$ 的父节点为 $c[x+lowbit(x)]$ ，可通过将 $x$ 每次减少 $lowbit(x)$ 直到 $0$ 反推回节点的儿子得到要查询的树状数组区间和；

int query(int x) {
	int tot = 0;
	while (x != 0) {
		tot += BIT[x];
		x -= lowbit(x);
	}
	return tot;
}

查询区间 $[l,r]$ 时，区间和即为 query(r) - query(l - 1) ；

2. 区间修改，单点查询

对于区间修改，可以通过差分进行，即修改 $[l,r]$ 时，只需将差分数组 $c$ 进行 $c[l]+x,c[r+1]-c$ 即可，又由于差分的前缀和为原数，所以可使用树状数组维护差分数组，最后查询时进行前缀和查询即可；

只需在单点修改，区间查询代码上修改初始化即可；

由于差分的前缀和为原数组，所以初始化可直接将 $a$ 数组值赋给 $BIT$ ;

void firstset(int n) {
	for (int i = 1; i <= n; i++) {
		BIT[i] = a[i] - a[i - lowbit(i)];
	}
	return;
}

修改 $[l,r]$ 加上 $x$ 时，由于维护的差分数组，应用 add (l, x), add(r + 1, -x) 修改；

查询元素 $x$ 时，由于是维护的差分数组，元素值即为 query(x) ；

3. 区间修改，区间查询

为区间修改，维护差分数组，由于是区间查询，不妨看一下差分与前缀和的关系；
$$\begin{array}{rl}sum[x]& =\sum _{i=1}^{x}a[i]\\ & =\sum _{i=1}^x\sum _{j=1}^{i}c[j]\\ & =\sum _{i=1}^x(x+1-i)\ast c[i]\\ & =\sum _{i=1}^x(x+1)\ast c[i]-\sum _{i=1}^{x}i\ast c[i]\end{array}$$
则可维护两个树状数组 $BIT1,BIT2$ ，分别维护 $c[i],c[i]\ast i$ 的前缀和，修改时将两个数组一起修改，查询时，将两个数组前缀和分别统计再相减；

由于 $BIT2$ 统计 $c[i]\ast i$ 前缀和，所以无法使用 $O(n)$ 的初始化，只能一个一个的加入树状数组；

void add(int i, int x) { // 修改
	int i1 = i;
	while (i <= n) {
		BIT1[i] += x;
		BIT2[i] += i1 * x;
		i += lowbit(i);
	}
	return;
}
int query(int x) { // 查询
	int yx = x, ans1 = 0, ans2 = 0;
	while (x != 0) {
		ans1 += (yx + 1) * BIT1[x];
		ans2 += BIT2[x];
		x -= lowbit(x);
	}
	return ans1 - ans2;
}
void firstset(int n) { // 初始化
	for (int i = 1; i <= n; i++) {
		add(i, a[i] - a[i - 1]);
	}
	return;
}

修改 $[l,r]$ 加上 $x$ 时，由于维护的差分数组，应用 add (l, x), add(r + 1, -x) 修改；

查询元素 $x$ 时，由于是维护的差分数组，元素值即为 query(r) - query(l - 1) ；

四、二维树状数组

可将二维树状数组每一行用一个一维数组进行统计，然后将二维数组每一行看作一个元素，使用一个一位树状数组维护每一行的树状数组；

即定义二维树状数组，将两维分别分为 $lo{g}_2(n)$ 个长度为 2 的幂的区间，分别对其进行区间内所有元素和的维护；

单点修改，区间查询

修改操作时，即通过两位分别进行更新即可；

查询时，通过二维前缀和得到矩阵元素和；

void add(int x, int y, int a) { // 修改
	int ry = y;
	while (x <= n) {
		y = ry;
		while (y <= m) {
			BIT[x][y] += a;
			y += lowbit(y);
		}
		x += lowbit(x);
	}
	return ;
}
int query (int x, int y) { // 查询
	int ans = 0, ry = y;
	while (x != 0) {
		y = ry;
		while (y != 0) {
			ans += BIT[x][y];
			y -= lowbit(y);
		}
		x -= lowbit(x);
	}
	return ans;
}
void firstset(int n, int m) { // 初始化
	for (int i = 1; i <= n; i++) {
		for (int j = 1; j <= m; j++) {
			add(i, j, a[i][j]);
		}
	}
	return;
}

查询左端点 $(x,y)$ ，右端点 $(x2,y2)$ 的值时，利用二维前缀和，query(x2, y2) - query(x - 1, y2) - query(x2, y - 1) + query(x - 1, y - 1) 即为答案；

区间修改，单点查询

利用二维差分进行区间修改；

即用树状数组维护原数组的差分数组；

修改左端点 $(x,y)$ ，右端点 $(x2,y2)$ 的值加上 $k$ 时，利用二维差分，add(x, y, k), add(x2 + 1, y, -k), add(x, y2 + 1, -k), add(x2 + 1, y2 + 1, k) 即可；

查询元素 $(x,y)$ 值时，利用二维差分，query(x, y) 即为答案；

区间修改，区间查询

对于二维差分与前缀和的关系如下；
$$\begin{array}{rl}sum[x][y]& =\sum _{i=1}^x\sum _{j=1}^{y}a[i][j]\\ & =\sum _{i=1}^x\sum _{j=1}^y\sum _{k=1}^i\sum _{l=1}^{j}c[k][l]\\ & =\sum _{i=1}^x\sum _{j=1}^{y}c[i][j]\ast (x+1-i)\ast (y+1-j)\\ & =(x+1)\ast (y+1)\ast \sum _{i=1}^x\sum _{j=1}^{y}c[i][j]-(y+1)\ast \sum _{i=1}^x\sum _{j=1}^{y}c[i][j]\ast i-(x+1)\ast \sum _{i=1}^x\sum _{j=1}^{y}c[i][j]\ast j+\sum _{i=1}^x\sum _{j=1}^{y}c[i][j]\ast i\ast j\end{array}$$

所以开四个树状数组分别维护 $c[i][j],c[i][j]\ast i,c[i][j]\ast j,c[i][j]\ast i\ast j$ ；

void add(int x, int y, int a) { // 修改
    int rx = x, ry = y;
    while (x <= n) {
    	y = ry;
    	while (y <= m) {
    		BIT1[x][y] += a;
        	BIT2[x][y] += rx * a;
        	BIT3[x][y] += ry * a;
        	BIT4[x][y] += rx * ry * a;
    		y += lowbit(y);
		}
        x += lowbit(x);
    }
    return;
}
int query(int x, int y) { // 查询
    int rx = x, ry = y, ans = 0;
    while (x > 0) {
    	y = ry;
        while (y > 0) {
        	ans += (rx + 1) * (ry + 1) * BIT1[x][y] - (rx + 1) * BIT3[x][y] - (ry + 1) * BIT2[x][y] + BIT4[x][y];
        	y -= lowbit(y);
		}
        x -= lowbit(x);
    }
    return ans;
}

修改左端点 $(x,y)$ ，右端点 $(x2,y2)$ 的值加上 $k$ 时，利用二维差分，add(x, y, k), add(x2 + 1, y, -k), add(x, y2 + 1, -k), add(x2 + 1, y2 + 1, k) 即可；

查询左端点 $(x,y)$ ，右端点 $(x2,y2)$ 的值时，利用二维前缀和，query(x2, y2) - query(x - 1, y2) - query(x2, y - 1) + query(x - 1, y - 1) 即为答案；

五、求逆序对

逆序对即为求 $i$ 以后比 $a[i]$ 小的数量，即可将数组倒序遍历，使用树状数组维护元素的个数，具体操作如下，

1. 建立空的树状数组 $BIT$ ；
2. 倒叙遍历序列 $a$ ；
   1. 查找树状数组中比 $a[i]$ 小的数个数，即 query(a[i] - 1) ，累加到 $ans$ 中；
   2. 将 $a[i]$ 加入树状数组中，以维护剩下元素的前缀和；

for (int i = n; i >= 1; i--) {
    ans += query(a[i] - 1);
    add(a[i], 1);
}

六、例题

楼兰图腾

分析

对于找 v 的个数时，若图形最低点为 $i$ ，则个数为下标 $1\sim i-1$ 中，坐标值比 $a[i]$ 大元素个数的与为下标 $i+1\sim n$ 中，坐标值比 $a[i]$ 大元素个数的积；

对于找 ^ 的个数时，若图形最高点为 $i$ ，则个数为下标 $1\sim i-1$ 中，坐标值比 $a[i]$ 小元素个数的与为下标 $i+1\sim n$ 中，坐标值比 $a[i]$ 小元素个数的积；

所以，用树状数组维护元素的个数，

1. 先顺序遍历，对于 $i$ 得到前 $i-1$ 个元素中比 $a[i]$ 大的元素个数 $l1[i]$ ，以及比 $a[i]$ 小的元素个数 $l2[i]$ ；
2. 清空树状数组，再顺序遍历，对于 $i$ 得到后 $i-1$ 个元素中比 $a[i]$ 大的元素个数 $r1[i]$ ，以及比 $a[i]$ 小的元素个数 $r2[i]$ ；
3. v 的个数即为 ${\sum }_{i=1}^{n}l1[i]\ast r1[i]$ ， ^ 的个数即为 ${\sum }_{i=1}^{n}l2[i]\ast r2[i]$ ；

代码

#include <cstdio>
#include <cstring>
#include <algorithm>
#define MAXN 1000005
using namespace std;
int n;
long long m, a[MAXN], BIT1[MAXN], BIT2[MAXN], l1[MAXN], l2[MAXN], r1[MAXN], r2[MAXN], ans1, ans2;
int lowbit(int x) { return x & (-x); }
void add(int i, long long a) {
	while (i <= m) {
		BIT1[i] += a;
		BIT2[i] += a;
		i += lowbit(i);
	}
	return;
}
long long query(int i) {
	int tot = 0;
	while (i != 0) {
		tot += BIT1[i];
		i -= lowbit(i);
	}
	return tot;
}
long long query1(int i) {
	long long tot = 0;
	while (i != 0) {
		tot += BIT2[i];
		i -= lowbit(i);
	}
	return tot;
}
int main() {
	scanf("%lld", &n);
	for (int i = 1; i <= n; i++) {
		scanf("%lld", &a[i]);
		m = max(m, a[i]);
	}
	for (int i = 1; i <= n; i++) {
		l1[i] = i - 1 - query(a[i]);
		l2[i] = query1(a[i] - 1);
		add(a[i], 1);
	}
	memset(BIT1, 0, sizeof(BIT1));
	memset(BIT2, 0, sizeof(BIT2));
	for (int i = n; i >= 1; i--) {
		r1[i] = n - i - query(a[i]);
		r2[i] = query1(a[i] - 1);
		add(a[i], 1);
	}
	for (int i = 1; i <= n; i++) {
		ans1 += l1[i] * r1[i];
		ans2 += l2[i] * r2[i];
	}
	printf("%lld %lld", ans1, ans2);
	return 0;
}