2-5 修理牧场 (35分，满分代码在文末，代码三)

原创已于 2022-11-18 12:19:35 修改 · 238 阅读

2 ·

CC 4.0 BY-SA版权

文章标签：

#c++ #算法 #开发语言

于 2022-11-18 10:44:28 首次发布

本文探讨如何通过编程解决农夫需要将长木头锯成多段以修补栅栏的问题，目的是寻找最小化的锯木成本。文章提供了三种不同的实现方案，包括模拟Huffman树和优先队列的方法，并对算法进行了逐步优化。

农夫要修理牧场的一段栅栏，他测量了栅栏，发现需要N块木头，每块木头长度为整数Li个长度单位，于是他购买了一条很长的、能锯成N块的木头，即该木头的长度是Li的总和。

但是农夫自己没有锯子，请人锯木的酬金跟这段木头的长度成正比。为简单起见，不妨就设酬金等于所锯木头的长度。例如，要将长度为20的木头锯成长度为8、7和5的三段，第一次锯木头花费20，将木头锯成12和8；第二次锯木头花费12，将长度为12的木头锯成7和5，总花费为32。如果第一次将木头锯成15和5，则第二次锯木头花费15，总花费为35（大于32）。

请编写程序帮助农夫计算将木头锯成N块的最少花费。

输入格式:

输入首先给出正整数N（≤104），表示要将木头锯成N块。第二行给出N个正整数（≤50），表示每段木块的长度。

输出格式:

输出一个整数，即将木头锯成N块的最少花费。

输入样例:

8
4 5 1 2 1 3 1 1

输出样例:

代码一（模拟huffman树）:

#include <stdio.h>
#include <stdlib.h>
#define MAX 10000000
int huffM[10050]={0},huffParent[10050]={0};

int main()
{
    int n;
    scanf("%d",&n);
    for(int i=0;i<n;i++)scanf("%d",&huffM[i]);

    int labalMin,labalSma,min,sma;
    int sum=0;
    for(int i=0;i<n-1;i++)
    {
        labalMin=labalSma=0;min=sma=MAX;
        for(int j=0;j<n+i;j++)
        {
            if(huffM[j]<min&&!huffParent[j])
            {

                sma=min;     labalSma=labalMin;
                min=huffM[j];labalMin=j;
            }
            else if(huffM[j]<sma&&!huffParent[j])
            {
                sma=huffM[j];labalSma=j;
            }
        }
        huffParent[labalMin]=1;huffParent[labalSma]=1;
        sum+=sma+min;
        huffM[n+i]=sma+min;
    }
    printf("%d",sum);
    return 0;
}

代码大数据测试点出现段错误，无法通过，原因未找到

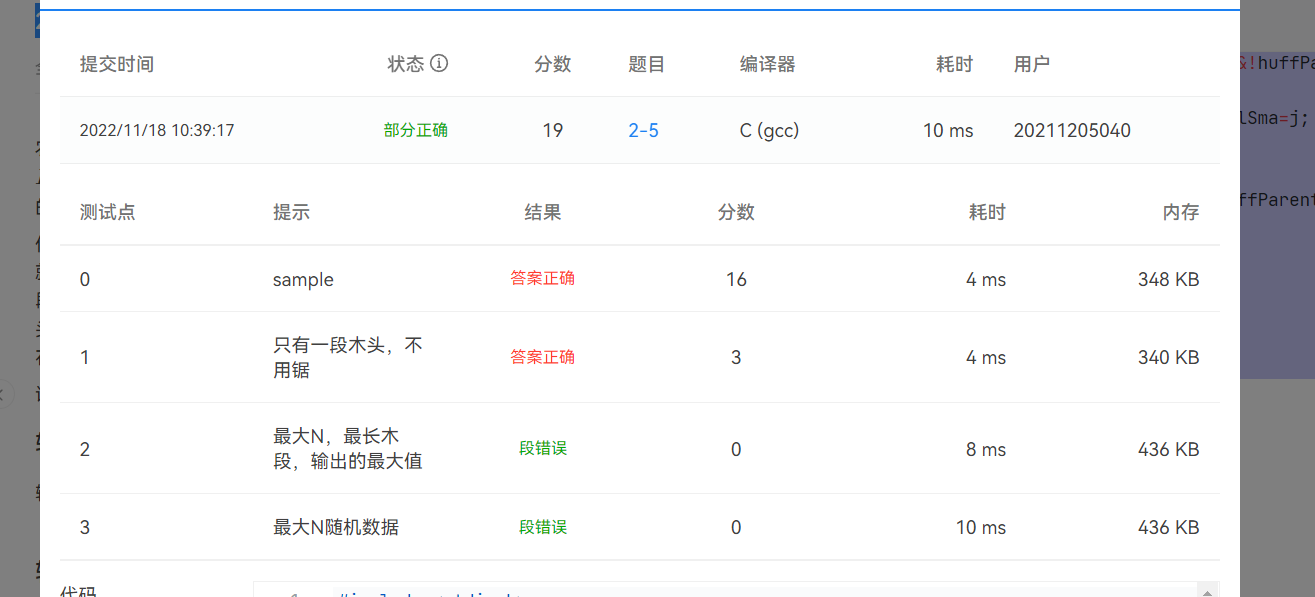
代码二（模拟优先队列）：

#include <stdio.h>
#include <stdlib.h>
int huffMTree[10015];

int cmp(const void *a,const void *b)
{
    return *(int*)b-*(int*)a;
}

int main()
{
    int sum=0,n,newData;
    scanf("%d",&n);

    for(int i=0;i<n;i++)scanf("%d",&huffMTree[i]);

    int go=n-1;
    for(int i=0;i<go;i++)
    {
        qsort(huffMTree,n,sizeof(huffMTree[0]),cmp);
        newData=huffMTree[n-1]+huffMTree[n-2];
        huffMTree[n-2]=newData;
        sum+=newData;
        n-=1;
    }
    printf("%d",sum);
    return 0;
}

这段代码大数据测试点也出现错误，无法通过，原因应该是我使用了降序排列，当数据较多而新增数据较小时，qsort插入新数值需要完全遍历数据（quickSort排序效率最低的情况），所以现在需要改写一下插入新数据的代码。

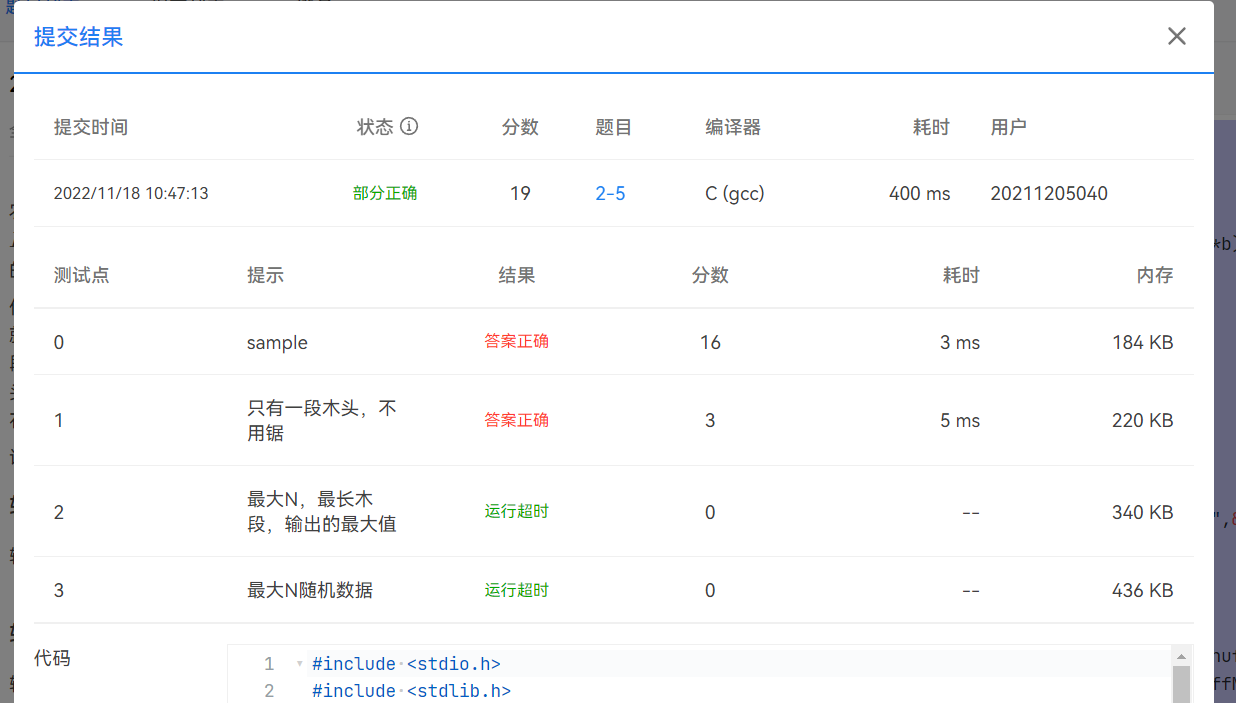
针对刚才想到的问题优化了一下新数据插入的算法，成功过了，以下为满分代码

代码三（模拟优先队列优化）：

#include <stdio.h>
#include <stdlib.h>
int huffMTree[10015];

int cmp(const void *a,const void *b)
{
    return *(int*)b-*(int*)a;
}

int main()
{
    int sum=0,n,newData;
    scanf("%d",&n);

    for(int i=0;i<n;i++)scanf("%d",&huffMTree[i]);
    qsort(huffMTree,n,sizeof(huffMTree[0]),cmp);//先对数据进行降序排序

    int go=n-1;
    for(int i=0;i<go;i++)
    {
        newData=huffMTree[n-1]+huffMTree[n-2];//新数据需要插入，应该从后往前搜索插入位置
        n-=2;
        for(int k=n-1;k>=0;k--)
        {
            if(k==0)
            {
                huffMTree[k+1]=huffMTree[k];
                huffMTree[k]=newData;break;
            }
            else if(huffMTree[k]<newData)huffMTree[k+1]=huffMTree[k];
            else
            {
                huffMTree[k+1]=huffMTree[k];
                huffMTree[k]=newData;break;
            }
        }
        sum+=newData;
        n+=1;
    }
    printf("%d",sum);
    return 0;
}