编译原理 [0x02][0x02] ==(3.3) 词法分析__确定有限自动机和非确定有限自动机

最新推荐文章于 2024-08-18 14:28:36 发布

原创最新推荐文章于 2024-08-18 14:28:36 发布 · 1.6k 阅读

9 ·

CC 4.0 BY-SA版权

编译原理专栏收录该内容

12 篇文章

订阅专栏

本文深入解析确定有限自动机(DFA)与非确定有限自动机(NFA)的基本概念、状态转换、产生语言及等价性。阐述了两者在状态集、弧标记、转换关系上的区别，并详细说明了NFA如何通过子集法转换为DFA，实现等价转换。

确定有限自动机（DFA）

确定有限自动机(Deterministic Finite Automata，DFA) M是一个五元式 M=(S, $\sum$ , f, S0, F)，其中：

1.S: 有穷状态集

2. $\sum$ ：输入字母表(有穷)

3.f : 状态转换函数，为S´S $\rightarrow$ S的单值部分映射，f(s，a)=s’表示：当现行状态为s，输入字符为a时，将状态转换到下一状态s’，s’称为s的一个后继状态

4. $S_{0}\in S$ 是唯一的一个初态

5.F $\subseteq$ S ：终态集(可空)

PS：根据图1.1.来说

1.有穷状态集即带圈圈的数字的集合

2.字母表即从一个数字圈圈变成下一个数字圈圈的条件的集合

3.状态转换函数就那个箭头，也就是怎么转换的具体过程

4.初态就是入口

5.终态就是出口

eg：

DFA M=( {0，1，2，3}，{a，b}，f，0，{3})，其中f定义如下：

f(0，a)=1 f(0，b)=2

f(1，a)=3 f(1，b)=2

f(2，a)=1 f(2，b)=3

f(3，a)=3 f(3，b)=3

图1.1

确定有限自动机产生语言

对于 $$\sum $^{*}$ 中的任何字a，若存在一条从初态到某一终态的道路，且这条路上所有弧上的标记符连接成的字等于a，则称a为DFA M所识别(接收) PS：括号忽略掉， $$\sum $^{*}$ = $\sum$ 的闭包

DFA M所识别的字的全体记为L(M)

PS：这句话就是说只要存在一条从入口到出口的路。这条路上的字母组成的字符串就能被该自动机识别并处理

eg：

这个识别的就是所有以00结尾的串也就是说，

该自动机M产生的语言是 L(M)={以00结尾的串}

再举例

以下哪个DFA能识别 { $\varepsilon$ }？

很显然，A 能够识别一个字 $\varepsilon$ 。因为系统初始处于初态q0，不读入任何字符也是停留在q0，而q0又是终态，所以相当于从初始状态q0出发，读入了长度为0字符串，停留在终止状态q0，也就是识别了 $\varepsilon$ 。或者从路径上理解，q0到q0就是一个从初态到终态的通路，通路上的标记构成的字符串就是 $\varepsilon$ 。

再来看看图B，B 能识别任什么字？因为系统初始处于初态q0，q0没有射出弧，无法读入任何字符而转入别的状态，而q0本身也不是终态，也不存在从初态到终态的 $\varepsilon$ 通路，连 $\varepsilon$ 也不能识别。所以B不能识别任何字，所以，识别的字的集合是空集。

非确定有限自动机（NFA）

定义：一个非确定有限自动机(Nondeterministic Finite Automata，NFA) M是一个五元式M=(S, $\sum$ , f, S0, F)，其中：

1.S: 有穷状态集

2. $\sum$ ：输入字母表(有穷)

3.f: 状态转换函数，为S´S* $\rightarrow$ $2^{S}$ 的部分映射

4. $S_{0}\in S$ 是非空的初态集

5.F $\subseteq$ S ：终态集(可空)

PS：与确定有限自动机不同的是，f 状态转换函数和它的初态可以有多个！

确定有限自动机的f是单值映射，也就是f的函数的转换条件只能是一个，比如说当输入字母a从状态1转换到状态2。

但是非确定有限最自动机的部分映射，即比如当输入a或者b的时候从状态1转换到状态2，即转换条件的数量

看下面eg的图可能比较容易理解

从状态图看NFA 和DFA的区别

NFA可以有多个初态
弧上的标记可以是S*中的一个字(甚至可以是一个正规式)，而不一定是单个字符
同一个字可能出现在同状态射出的多条弧上
DFA是NFA的特例

eg：

NFA M1

DFA M2

非确定有限自动机产生语言

同确定有限自动机一样产生方式类似，只不过需要忽略 $\varepsilon$

DFA和NFA

定义：对于任何两个有限自动机M和M’，如果L(M)=L(M’)，则称M与M’等价
自动机理论中一个重要的结论：判定两个自动机等价性的算法是存在的
对于每个NFA M存在一个DFA M’，使得 L(M)=L(M’)
DFA与NFA识别能力相同，故二者可以相互转化

NFA

DFA

初始状态

不唯一

唯一

弧上的标记

字(单字符字、e)

字符

转换关系

非确定

确定

等价性证明略

子集法

NFA确定化--子集法

设I是的状态集的一个子集，定义I的 $\varepsilon$ -闭包 $\varepsilon$ -closure(I)为:
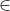
若s $\in$ I，则s $\in$ $\varepsilon$ -closure(I)；
若s $\in$ I，则从s出发经过任意条 $\varepsilon$ 弧而能到达的任何状态s’都属于 $\varepsilon$ -closure(I) 即，
$\varepsilon$ -closure(I)=I $\bigcup$ {s’ | 从某个s $\in$ I出发经过任意条 $\varepsilon$ 弧能到达s’ }

设a是S中的一个字符，定义

$I_{a}$ = $\varepsilon$ -closure(J)

其中，J为I中的某个状态出发经过一条a弧而到达的状态集合。

具体计算

确定化：不失一般性，设字母表只包含两个 a 和b，我们构造一张计算状态集的转换表:
首先，置第1行第1列为 $\varepsilon$ -closure({X})求出这一列的Ia，Ib；
然后，检查这两个Ia，Ib，看它们是否已在表中的第一列中出现，把未曾出现的填入后面的空行的第1列上，求出每行第2，3列上的集合...
重复上述过程，直到所有第2，3列子集全部出现在第一列为止

eg：

解题步骤拆解

1.首先取出状态X作为第一次计算 $\varepsilon$ -closure({X}),根据条件空字，（第一次条件就是计算空字），找与X直接相连的，且条件为 $\varepsilon$ ，得到 {X,1,2}，

2.再根据第一次得到的{X,1,2}，把这个集合内的所有元素一一取出来找符合条件的，先找条件为a的，X没有，1有{1}，2有{5}，再寻找条件a后条件为 $\varepsilon$ 的，1通过条件a得到自身，1后面有一个条件为 $\varepsilon$ 的得到2,5后面是a不符合（几个 $\varepsilon$ 连着都行），将X得到的集合和1、2得到的集合相加即得到表里的{1,5,2}

(前面条件是 $\varepsilon$ 不行)

3.Ib同理可得，然后到第二行了，第二行第一列就把上一行的Ia放到此处重复，第三行第一列就是把第一行第一列的Ib放到这里重复步骤1、2

4.直到Ia和Ib中的元素都在第一列出现为止

NFA转换DFA

把表看成状态转换矩阵，子集视为状态（图1.2）
转换表唯一刻划了一个确定的有限自动机M
初态是 $\varepsilon$ -closure({X})
终态是含有原终态Y的子集
不难看出，这个DFA M与M’等价
对于每个NFA M存在一个DFA M ’ ，使得 L(M)=L(M’)（图1.3）
NFA和DFA等价

图1.2 转换表