Optimization 最优化
引言
在机器学习中,通常构造出一个带有约束条件的目标函数进行优化,学习最优化方法有助于机器学习算法。本章节借助天津大学网课(https://www.xuetangx.com/course/ecust13051002148/4231479?channel=learn_title)对部分最优化方法归纳总结。
学习时间:2021/06/21-2021/06/26
文章结构:
1 概念
最优化
最优化问题的求解步骤为建模、求极值。
最优化问题的标准形式:
min x ∈ R n f ( x ) \underset{\boldsymbol{x}\in R^n}{\min}\,\,f\left( \boldsymbol{x} \right) x∈Rnminf(x)
s . t . g u ( x ) ⩽ 0 , u = 1 , 2 , . . . m s.t. g_u\left( \boldsymbol{x} \right) \leqslant 0 ,u=1,2,...m s.t.gu(x)⩽0,u=1,2,...m
h v ( x ) = 0 , v = 1 , 2 , . . . p ( p < n ) h_v\left( \boldsymbol{x} \right) =0,v=1,2,...p\left( p<n \right) hv(x)=0,v=1,2,...p(p<n)
线性/非线性规划
线性规划:目标函数和约束条件都为线性函数
非线性规划:目标函数和约束条件不都为线性函数
目标函数等值线
具有相同目标函数值的设计点(决策变量)构成的平面曲线。当决策变量大于2时,为等值面,超曲面。
用平行于x1x2平面的平面截取f(x),界面边界在x1x2平面的投影即为其中一条等值线。如下图:
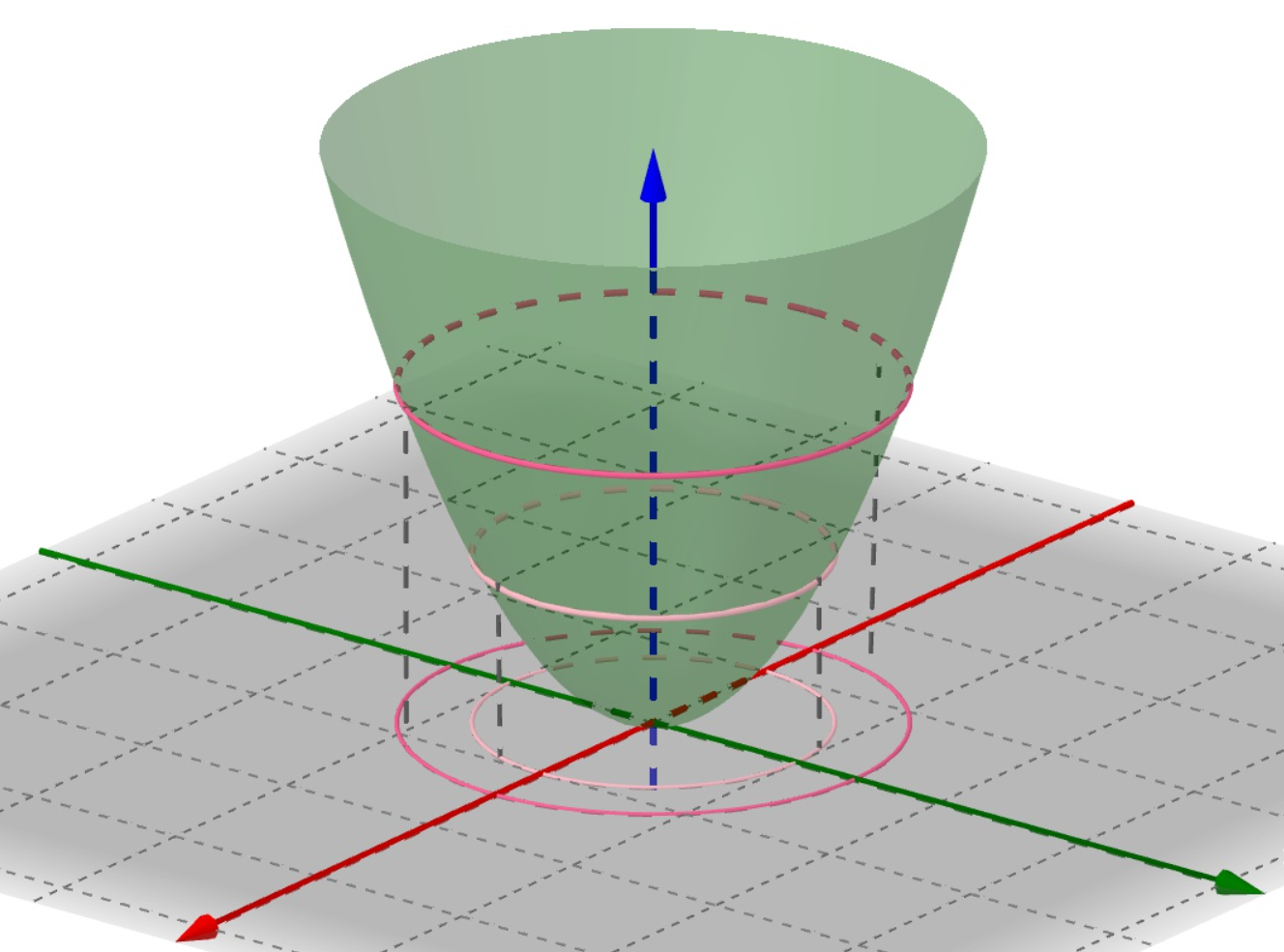
可行域
可行域:受约束函数的限制,目标函数的可行域可表示为多个不等式约束函数 g u ( x ) g_u\left( \boldsymbol{x} \right) gu(x)围成的区域,且当有等式约束时,可行域为 h v ( x ) h_v\left( \boldsymbol{x} \right) hv(x)上在不等式约束函数围成区域内的点。
可行域的确定见下图(当等式约束数量p大于决策变量数量n时,不一定有可行域,因为多条直线必要穿过同一点):
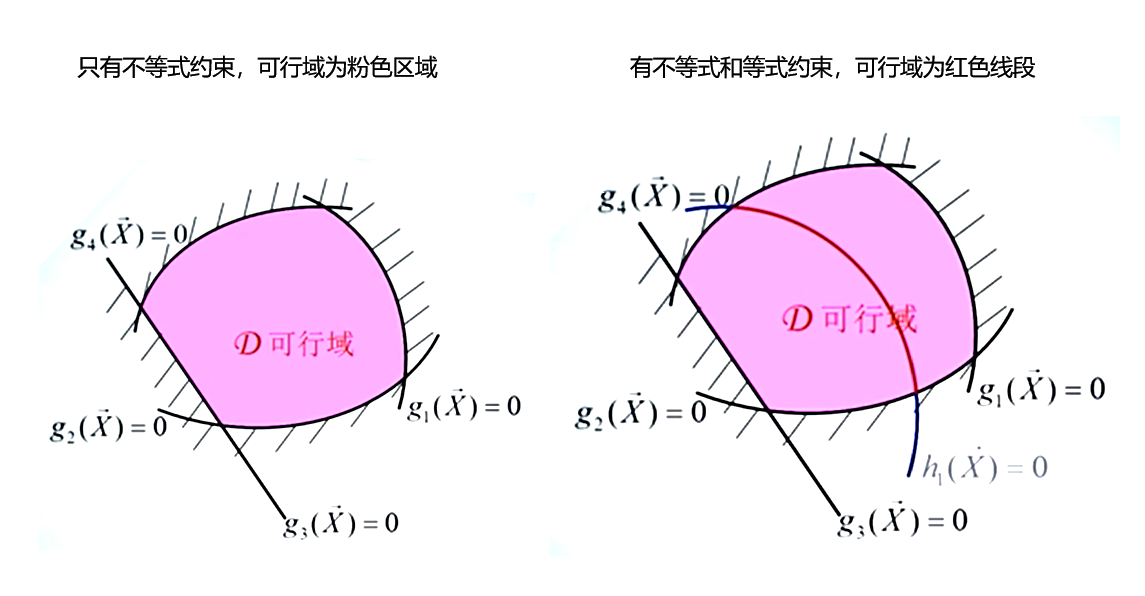
梯度/海森矩阵
在单变量函数中,梯度是函数的微分,代表着函数在某个给定点的切线斜率。
在多变量函数中,梯度是空间内的一个向量,梯度的方向是函数在给定点局部上升或下降最快的方向,相当于一元函数的一次导 数。
海森矩阵(Hessian Matrix)
海森矩阵相当于多元函数求二次导数组成的矩阵,由于 ∂ 2 f ∂ x 1 ∂ x 2 \frac{\partial ^2f}{\partial x_1\partial x_2} ∂x1∂x2∂2f= ∂ 2 f ∂ x 2 ∂ x 1 \frac{\partial ^2f}{\partial x_2\partial x_1} ∂x2∂x1∂2f,所以海森矩阵是对称矩阵,计算时只需算下三角或上三角。
n元函数的梯度、海森矩阵的定义及计算示例见下图:

泰勒展开
泰勒展示式在函数某一点附近用简单多项式近似复杂函数,带来了分析计算上的便利。
一元函数在 x 0 x_0 x0处的的泰勒式展开为:
f ( x ) = f ( x 0 ) + f ′ ( x 0 ) ( x − x 0 ) + 1 2 ! f ′ ′ ( x 0 ) ( x − x 0 ) 2 . . . + 1 n ! f n ( x 0 ) ( x − x 0 ) n + C f\left( x \right) =f\left( x_0 \right) +f'\left( x_0 \right) \left( x-x_0 \right) +\frac{1}{2!}f''\left( x_0 \right) \left( x-x_0 \right) ^2...+\frac{1}{n!}f^n\left( x_0 \right) \left( x-x_0 \right) ^n+C f(x)=f(x0)+f′(x0)(x−x0)+2!1f′′(x0)(x−x0)2...+n!1fn(x0)(x−x0)n+C
多元函数在 x 0 \boldsymbol{x}_0 x0处的泰勒级数展开(只取前两项)为:
f ( x ) ≈ f ( x 0 ) + ∇ f ( x ) T ( x − x 0 ) ∇ f ( x ) + 1 2 ( x − x 0 ) T H ( x ) ( x − x 0 ) f\left( \boldsymbol{x} \right) \approx f\left( \boldsymbol{x}_0 \right) +\nabla f\left( \boldsymbol{x} \right) ^{\mathrm{T}}\left( \boldsymbol{x}-\boldsymbol{x}_0 \right) \nabla f\left( \boldsymbol{x} \right) +\frac{1}{2}\left( \boldsymbol{x}-\boldsymbol{x}_0 \right) ^{\mathrm{T}}H\left( \boldsymbol{x} \right) \left( \boldsymbol{x}-\boldsymbol{x}_0 \right) f(x)≈f(x0)+∇f(x)T(x−x0)∇f(x)+21(x−x0)TH(x)(x−x0)
其中 H ( x ) H\left( \boldsymbol{x} \right) H(x)为对于x0处的海森矩阵。
正定、半正定、负定矩阵
在线性代数中,正定矩阵(positive definite matrix)对应复数中的正实数。半正定矩阵(positive semi-define matrix)对应复数中的非负实数,负定矩阵(negative definite matrix)对于复数中的负数。
正定矩阵的定义: 若 n 阶实对称方阵 A ,对于任意的 n 维非零向量 x , 满足 x T A x > 0 \boldsymbol{x}^{\mathrm{T}}\boldsymbol{Ax}>0 xTAx>0 ,则方阵 A 为正定矩阵。
半正定矩阵的定义: 若 n 阶实对称方阵 A ,对于任意的 n 维向量 x , 满足 x T A x ⩾ 0 \boldsymbol{x}^{\mathrm{T}}\boldsymbol{Ax}\geqslant 0 xTAx⩾0 ,则方阵 A 为半正定矩阵。
正定矩阵的判断: n 阶方阵 A 的各阶顺序主子式(左上角K阶方阵构成的行列式)均大于0。
负定矩阵的判断: n 阶方阵 A 的各阶顺序主子式(左上角K阶方阵构成的行列式)负正相间(奇数阶小于0,偶数阶大于0)。
不定矩阵的判断:非正定非负定即为不定矩阵。
协方差矩阵要求是半正定的。
凸集/凸函数/凸规划
一元凸函数定义:若函数 f(x) 曲线上任意两点的连线用在 f(x) 曲线上方,则 f(x) 为凸函数 。
在几何中,存在关系 f ( x ) ⩽ Y f\left( \boldsymbol{x} \right) \leqslant Y f(x)⩽Y

凸集定义:集合D中任意两点 x 1 \boldsymbol{x}_1 x1、 x 2 \boldsymbol{x}_2 x2的连线仍在D内,则D内凸集,否则为非凸集。
多元凸函数定义:f(x)定义域为凸集,对任意实数 0 ⩽ λ ⩽ 1 0\leqslant \lambda \leqslant 1 0⩽λ⩽1,,D中任意两点 x 1 、 x 2 \boldsymbol{x}_{\boldsymbol{1}}\text{、}\boldsymbol{x}_2 x1、x2均存在:
f [ λ x 1 + ( 1 − λ ) x 2 ] ⩽ λ f ( x 1 ) + ( 1 − λ ) f ( x 2 ) 0 ⩽ λ ⩽ 1 {\ f\left[ \lambda \boldsymbol{x}_{\boldsymbol{1}}+\left( 1-\lambda \right) \boldsymbol{x}_{\boldsymbol{2}} \right] \leqslant \lambda f\left( \boldsymbol{x}_{\boldsymbol{1}} \right) +\left( 1-\lambda \right) f\left( \boldsymbol{x}_{\boldsymbol{2}} \right) \,\,\ \ \ }0\leqslant \lambda \leqslant 1 f[λx1+(1−λ)x2]⩽λf(x1)+(1−λ)f(x2) 0⩽λ⩽1
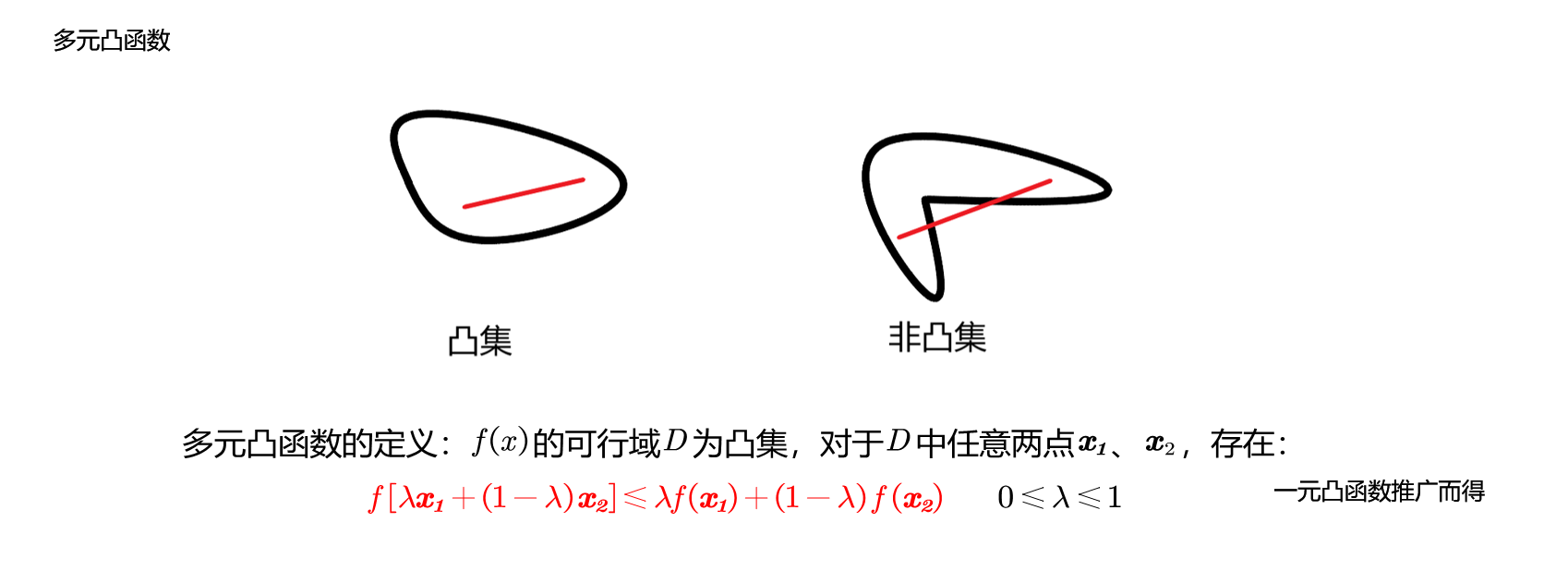
多元凸函数的判定条件为: f ( x ) f\left( \boldsymbol{x} \right) f(x)的海森矩阵为半正定矩阵。
凸规划定义:对于优化问题
min x ∈ R n f ( x ) \underset{\boldsymbol{x}\in R^n}{\min}\,\,f\left( \boldsymbol{x} \right) x∈Rnminf(x)
s . t . g u ( x ) ⩽ 0 , u = 1 , 2 , . . . m s.t. g_u\left( \boldsymbol{x} \right) \leqslant 0 ,u=1,2,...m s.t.gu(x)⩽0,u=1,2,...m
当f(x),g(x)均为凸函数时,优化问题为凸规划问题。
凸规划问题的性质:
- f(x)等值线呈大圈套小圈的形式
- 可行域为凸集
- 局部最小点一定是全局最优解
算法收敛性
对于式
lim k → ∞ ∣ ∣ x k + 1 − x ∗ ∣ ∣ ∣ ∣ x k − x ∗ ∣ ∣ β = σ ( 0 < σ < 1 ) \underset{k\rightarrow \infty}{\lim}\frac{||\boldsymbol{x}_{k+1}-\boldsymbol{x}^*||}{||\boldsymbol{x}_k-\boldsymbol{x}^*||^{\beta}}=\sigma \,\, \left( 0<\sigma <1 \right)





 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章

















 716
716

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








