一、简介
回溯法是一种通过逐步构造解,并在发现当前解不满足问题要求时回退、尝试其他可能性的算法。回溯法通过逐步构建解并不断进行验证,当发现当前解无法继续满足约束条件时,算法会回溯到上一步进行其他选择,直到找到一个符合要求的解或穷尽所有可能。
回溯法的核心步骤:
1、解空间:问题的所有可能组成的空间。
2、选择:逐步构造解,每一步根据一定的规则尝试一个可行的选择。
3、验证约束:检查当前部分解是否满足问题的约束条件
4、回溯:如果当前选择导致不满足约束条件,则回退到上一个状态,尝试其他可能性。
5、终止条件:当找到一个可行解或遍历了整个解空间时,算法终止。
二、回溯方式
1、递归回溯
2、迭代回溯
3、子集树与排列树
三、算法优势/适用场景
1、八皇后问题
2、数独
3、全排列问题
4、图的着色问题
四、例题(C++,随缘更新)
1、子集和问题
题目来源:计算机算法设计与分析(第五版)王晓东
问题描述:子集和问题的一个实例为<S,t>。其中,S={x1,x2,…,x„}是一个正整数的集合,c是一个正整数。子集和问题判定是否存在S的一个子集S1,使得S1所有元素的和等于c。试设计一个解子集和问题的回溯法。
数据输入:第1行有2个正整数n和c,n表示S的大小,c是子集和的目标值。接下来的1行中,有n个正整数,表示集合S中的元素。
结果输出:输出子集和问题的解。当问题无解时,输出“No Solution!”
回溯方式:采用递归回溯的方式。
解空间:在这个问题中,解空间就是集合S中所有可能的子集,对于集合中的每个元素只有两种状态:选中和不选中,因此,解空间的大小为2^n。
选择:在每一步做出选择,即是否包含当前元素。
检查当前解:当当前选择的子集之和等于目标值c时,说明找到一个解,可以输出该子集。
剪枝:如果当前部分的和已经大于目标值c或者解空间已经遍历完,则停止对该路径的继续探索,回溯到上一步,进行下一种选择。
代码:
#include <iostream>
#include <vector>
using namespace std;
void findSub(const vector<int>& s, vector<int>& sub, int index, int current, int target, bool& found){
//这里题目中只输出了一个解,那么就把终止条件放在前面。
//如果把输出放在前面的话会输出所有的解。
//终止条件:找到一
if(index >=s.size() || current > target || found)
{
return;
}
if(current == target)
{
found = true;
for(int i=0;i<sub.size();++i)
{
cout << sub[i] << " ";
}
return;
}
//选择当前元素
sub.push_back(s[index]);
findSub(s, sub, index + 1, current+s[index], target, found); //递归
sub.pop_back();//回溯
//不选择当前元素
findSub(s, sub, index + 1, current, target, found);
}
int main(int argc, char** argv) {
int n, c;
cin >> n >> c;
int a[n];
//输入
vector<int> s(n);
for(int i=0; i<n; ++i)
{
cin >> s[i];
}
vector<int> sub;
bool found = false;
findSub(s,sub,0,0,c,found);
if(!found) {
cout << "No Solution!" << endl;
}
return 0;
}
复杂度分析:
时间复杂度:最坏情况就是遍历解空间的每一个节点,应该是O(2^n)
空间复杂度:递归深度最大为n,子集sub最大也为n,空间复杂度为O(n)
2、最小长度电路板排列问题
题目来源:计算机算法设计与分析(第五版)王晓东
问题描述:最小长度电路板排列问题是大规模电子系统设计中提出的实际问题。该问题的提法是,将n块电路板以最佳排列方案插入带有n个插槽的机箱中。n块电路板的不同的排列方式对应于不同的电路板插入方案。
设 B={1,2.…,n}是n块电路板的集合。集合L={N1,N2,…,Nm}是n块电路板的m个连接块。其中每个连接块Ni是B的一个子集,且Ni中的电路板用同一根导线连接在一起。在最小长度电路板排列问题中,连接块的长度是指该连接块中第1块电路板到最后1块电路板之间的距离。
试设计一个回溯法,找出所给n个电路板的最佳排列,使得m个连接块中最大长度达到最小。
数据输入:第1行有2个正整数n和m(1≤m,n≤20),接下来的n行中,每行有m个数。第k行的第j个数为0表示电路板k不在连接块j中,为1表示电路板k在连接块i中。
结果输出:输出的第一行是最小长度,接下来的1行是最佳排列
输入示例: 输出示例:
8 5 4
1 1 1 1 1 5 4 3 1 6 2 8 7
0 1 0 1 0
0 1 1 1 0
1 0 1 1 0
1 0 1 0 0
1 1 0 1 0
0 0 0 0 1
0 1 0 0 1
样例分析:长度4是如何计算的?
连接块的长度是指该连接块中第1块电路板到最后1块电路板之间的距离,即最后一个电路板所在位置-第一个电路板所在位置,以输出的排列{5,4,3,1,6,2,8,7}为例。
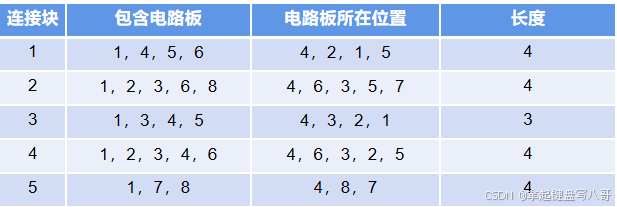
回溯思路:
解空间:所有电路板排列的集合,即n!

选择路径:在每一步,选择一个尚未放置的电路板,并将其插入当前排列中。 检查:在排列完成后,计算排列中所有连接块的最大距离,记录最大长度。
回溯方式:递归调用:完成路径选择后,递归处理下一个插槽的电路板选择。 递归回溯:从当前排列中移除该电路板,并选择其他电路板,尝试新的排列。
剪枝:如果当前排列的长度已经大于或等于已知的最小长度,则停止该路径的继续生成。
回溯示例:


代码实现:
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
int n, m; // n块电路板,m个连接块
vector<vector<int>> connection; // 连接块矩阵
vector<int> best; // 最佳排列
int min_length = INT_MAX; // 最小长度
// 计算当前排列的最大连接块长度
int calculate(const vector<int>& perm) {
int max_length = 0;
// 遍历每个连接块,计算每个连接块的长度
for (int j = 0; j < m; ++j) {
//初始化最小位置和最大位置
int first = -1, last = -1;
// 找到当前排列中连接块j的第一个和最后一个电路板的位置
for (int i = 0; i < perm.size(); ++i) {
if (connection[perm[i] - 1][j] == 1) {
if (first == -1) first = i;
last = i;
}
}
if (first != -1 && last != -1) {
//计算当前连接块的长度
int length = last - first;
//所有连接块的最大长度
max_length = max(max_length, length);
}
}
return max_length;
}
// 回溯搜索所有电路板的排列
void backtrack(vector<int>& perm, vector<bool>& visited, int current) {
//完成一个排列
if (perm.size() == n) {
int max_length = calculate(perm);
if (max_length < min_length) {
min_length = max_length;
best = perm;
}
return;
}
//剪枝:计算当前排列的部分最大长度,若已经超过当前最小长度,则跳过该排列
if(current >= min_length)
{
return;
}
//路径选择
for (int i = 1; i <= n; ++i) {
//如果电路板没有被放置,则放置第i个电路板
if (!visited[i]) {
visited[i] = true;
perm.push_back(i);
//更新当前长度
int new_length = calculate(perm);
backtrack(perm,visited,new_length);
perm.pop_back();
visited[i] = false;
}
}
}
int main() {
cin >> n >> m;
//设置连接矩阵的大小为n,每个单元是一个大小为m的vector数组
connection.resize(n, vector<int>(m));
for (int i = 0; i < n; ++i) {
for (int j = 0; j < m; ++j) {
cin >> connection[i][j];
}
}
vector<int> perm; // 当前排列
vector<bool> visited(n + 1, false); // 标记每块电路板是否已经访问
backtrack(perm, visited,0);//初始最大长度为0
// 输出结果
cout << min_length << endl;
for (int i = 0; i < best.size(); ++i) {
cout << best[i] << " ";
}
cout << endl;
return 0;
}
3、最小重量机器设计问题
题目来源:计算机算法设计与分析(第五版)王晓东
问题描述:设某一机器由n个部件组成,每种部件都可以从m个不同的供应商处购得。设w是从供应商j处购得的部件i的重量,c是相应的价格。试设计一个算法,给出总价格不超过d的最小重量机器设计。
数据输入:第一行有3个正整数n、m和d。接下来的2n行,每行n个数。前n行是c,后n行是w。
结果输出:将计算的最小重量及每个部件的供应商输出
输入示例: 输出示例:
3 3 4 4
1 2 3 1 3 1
3 2 1
2 2 2
1 2 3
3 2 1
2 2 2
解空间:一共需要n个部件,每个部件都可以从m个不同的供应商处购得,共有m^n种情况。
路径选择:递归选择每个部件的供应商,更新当前的总价格和总重量。
剪枝:如果当前价格已经超过预算d,则停止当前路劲的搜索。
更新最优解:如果所有部件已经选择完成且总价格并不超过d,则检查当前组合的总重量是否是最小的,如果是,则更新最优解。
代码实现:
#include <iostream>
#include <vector>
using namespace std;
int n, m, d; // n 部件数量, m 供应商数量, d 预算
vector<vector<int>> prices; // 每个部件从每个供应商购买的价格矩阵
vector<vector<int>> weights; // 每个部件从每个供应商购买的重量矩阵
vector<int> best_suppliers; // 最优的供应商选择
int min_weight = INT_MAX; // 当前最小重量
// 回溯函数
void findMinWeight(int part, int current_price, int current_weight, vector<int>& suppliers) {
// 基本条件:当所有部件的供应商都选定时,检查是否满足预算并更新最小重量
if (part == n) {
if (current_price <= d && current_weight < min_weight) {
min_weight = current_weight;
best_suppliers = suppliers;
}
return;
}
// 遍历每个供应商,尝试选择该供应商提供的部件
for (int j = 0; j < m; ++j) {
int price = prices[part][j];
int weight = weights[part][j];
// 剪枝条件:如果当前总价格超过预算,则不继续探索
if (current_price + price <= d) {
suppliers[part] = j + 1; // 记录当前部件的供应商(+1是为了表示供应商编号从1开始)
findMinWeight(part + 1, current_price + price, current_weight + weight, suppliers);
}
}
}
int main() {
cin >> n >> m >> d;
// 输入价格矩阵
prices.resize(n, vector<int>(m));
for (int i = 0; i < n; ++i) {
for (int j = 0; j < m; ++j) {
cin >> prices[i][j];
}
}
// 输入重量矩阵
weights.resize(n, vector<int>(m));
for (int i = 0; i < n; ++i) {
for (int j = 0; j < m; ++j) {
cin >> weights[i][j];
}
}
vector<int> suppliers(n); // 当前选择的供应商方案
// 进行回溯搜索
findMinWeight(0, 0, 0, suppliers);
// 输出结果
if (min_weight == INT_MAX) {
cout << "No solution!" << endl;
} else {
cout << min_weight << endl;
for (int i = 0; i < n; ++i) {
cout << best_suppliers[i] << " ";
}
cout << endl;
}
return 0;
}





















 693
693

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








