BA问题（一）

三维重建中的稀疏束调整(BA)解析

最新推荐文章于 2025-03-25 10:57:40 发布

原创最新推荐文章于 2025-03-25 10:57:40 发布 · 2.5k 阅读

3 ·

CC 4.0 BY-SA版权

本文详细介绍了束调整(BA)问题，本质是通过最小化重投影误差来优化三维结构和相机参数。BA是非线性最小二乘问题，常使用Levenberg-Marquardt算法求解，尤其是在考虑稀疏性的情况下能显著减少计算量。BA迭代过程中，利用稀疏性构建线性系统，并给出了稀疏BA迭代步长的算法求解流程。

部署运行你感兴趣的模型镜像

一、BA问题（本质：最小化重投影误差）

束调整（BA）是SaM的关键组成部分，几乎总是作为SaM的最后一步使用。
这是一个三维结构和观察参数（相机姿态、内部校准和径向畸变参数）的优化问题，这些参数同时被优化以最小化重新投影误差。
BA是假设零均值高斯图像噪声的ML估计量。
BA归结为一个非常大的非线性最小二乘问题，通常用Levenberg-Marquardt（LM）算法求解。
Std-LM涉及线性系统的重复解，每一个线性系统具有O（N3）时间和O（N2）存储复杂度。
LM需要求解的线性系统具有稀疏块结构。
这是因为某个点在某个相机上的投影不依赖于任何其他点或相机的参数。
一种处理BA的方案，它利用稀疏性来节省大量的计算量。一个ANSI C软件库（称为sba）实现了这个方案，并已在GNU GPL下公开提供。

二、BA迭代

n个三维物点，围绕这些点拍摄m张照片，第j张图片上看到的第i个物点为Xij。更具体的说：每个相机j用向量aj表示，每个三维物点i用向量bi表示。则BA核心问题即为：

$\min_{{a}_j ,{b}_i} \sum_{i=1}^{n} \sum_{j=1}^{m} {v}_i_j d{(Q({a}_j ,{b}_i),{x}_i_j)}^2$

其中， $Q({a}_j ,{b}_i)$ 是点i在图像j上的预测投影。函数d(x,y)表示观测的图像坐标与预测图像坐标间的欧氏距离。若点i在图像j中可见，则 ${v}_i_j$ =1。

2.用向量P代表m个投影矩阵和那个三维物点所有参数：

$P={({a}_1 ^T ,.....,{a}_m ^T ,.....{b}_1 ^T ,.....,{b}_n^T )}^T,P\in {R}^m$

用向量X表示所有图像内所有物点观测坐标：

$X={({x}_1_1^T,...,{x}_1_m^T,{x}_2_1^T,...,{x}_2_m^T,...,{x}_n_1^T,...,{x}_n_m^T)}^T,X\in{R}^n$

3.利用投影关系X‘=f(P)。每组参数的预测向量为：

$X={({x}_1_1^{'T},...,{x}_1_m^{'T},{x}_2_1^{'T},...,{x}_2_m^{'T},...,{x}_n_1^{'T},...,{x}_n_m^{'T})}^T,X^{'}\in{R}^n$

其中 ${x}_i_j^{'}=Q({a}_j ,{b}_i)$ ,表示预测投影坐标。

4.因此转化为一个非线性最小二乘问题：

$\sum_{i=1}^{n} \sum_{j=1}^{m} \left \| \epsilon _i_j \right \|^2 =\left \| X-X^{'} \right \|^2$

5.对应的雅可比矩阵：

$J=\frac{\partial {X}^{'}}{\partial x}=[\frac{\partial {X}^{'}}{\partial a}|\frac{\partial {X}^{'}}{\partial b}]=[A|B]$

LM迭代步长为：

$({\delta }_a^T ,\delta_b^T)^T$

正规方程化为：

$[\frac{A^TA |A^TB}{B^TA|B^TB}](\frac{\delta_a }{\delta_b })=(\frac{A^T\epsilon }{B^T\epsilon }), \frac{\partial x_i_j^{'}}{\partial a_k}=0,\forall j\neq k; \frac{\partial x_i_j^{'}}{\partial b_k}=0,\forall i\neq k$

例如：n=4,m=3

$X=({x}_1_1^{'T},{x}_1_2^{'T},{x}_1_3^{'T},{x}_2_1^{'T},{x}_2_2^{'T},{x}_2_3^{'T},{x}_3_1^{'T},{x}_3_2^{'T},{x}_3_3^{'T},{x}_4_1^{'T},{x}_4_2^{'T},{x}_4_3^{'T})^T$

$P=({a}_1^T,{a}_2^T,{a}_3^T,{b}_1^T,{b}_2^T,{b}_3^T,{b}_4^T)^T$

$\delta =({\delta }_a_1^T,{\delta }_a_2^T,{\delta }_a_3^T,{\delta }_b_1^T,{\delta }_b_2^T,{\delta }_b_3^T,{\delta }_b_4^T)^T$

$J=\frac{\partial X^{'}}{\partial P}=\begin{bmatrix} A_1_1 & 0 & 0 & B_1_1 & 0 & 0 & 0 \\ 0& A_1_2& 0 & B_1_2 & 0 & 0& 0\\ 0& 0& A_1_3& B_1_3& 0& 0& 0\\ A_2_1 & 0 & 0 & 0 & B_2_1 & 0 & 0 \\ 0& A_2_2& 0 & 0& B_2_2 & 0& 0\\ 0& 0& A_2_3& 0& B_2_3& 0& 0\\ A_3_1 & 0 & 0 & 0 &0 & B_3_1& 0 \\ 0& A_3_2& 0 & 0& 0 & B_3_2& 0\\ 0& 0& A_3_3& 0& 0& B_3_3& 0\\ A_4_1 & 0 & 0 & 0& 0 & 0 & B_4_1 \\ 0& A_4_2& 0 & 0& 0 & 0& B_4_2 \\ 0& 0& A_4_3& 0& 0& 0& B_4_3\\ \end{bmatrix}$

$J^TJ=\begin{bmatrix} U_1 & 0 & 0 & W_1_1 & W_2_1 & W_3_1 & W_4_1\\ 0& U_2& 0& W_1_2 & W_2_2 & W_3_2& W_4_2\\ 0& 0& U_3& W_1_3& W_2_3& W_3_3 & W_4_3\\ W_1_1^T& W_1_2^T & W_1_3^T & V_1 & 0& 0& 0\\ W_2_1^T& W_2_2^T & W_2_3^T & 0 & V_2& 0& 0\\ W_3_1^T& W_3_2^T & W_3_3^T & 0& 0& V_3& 0\\ W_4_1^T& W_4_2^T & W_4_3^T & 0& 0& 0& V_4\\ \end{bmatrix}=\begin{bmatrix} U & W\\ W^T& V \end{bmatrix}$

其中：

${U}_j=\sum_{i=1}^{4}{A}_i_j^T A_i_j$

$V_i=\sum_{j=1}^{3}B_i_j^T B_i_j$

$W_i_j=A_i_j^T B_i_j$

6.矩阵为992×992，黑色像素表示非零元素:

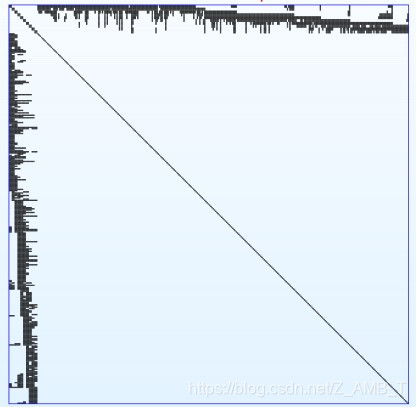
7.增广法方程形式为：

$(J^TJ+\mu I)\delta _p=J^T\epsilon$

$\begin{bmatrix} U^* &W \\ W^T&V^* \end{bmatrix}\cdot \begin{bmatrix} \delta_a\\ \delta_b \end{bmatrix}=\begin{bmatrix} \epsilon _a\\ \epsilon _b \end{bmatrix}$

对于上述方程两边同时左乘：

$\begin{bmatrix} I & -WV^{*-1}\\ 0&I \end{bmatrix}$

化为：

$(U^*-WV^{*-1}W^T)\delta_a=\epsilon _a-WV^{*-1}\epsilon_b$ 由此确定 $\delta_a$

将 $\delta_a$ 反代入上式，即可求得 $\delta_b$ ：

$V^*\delta_b=\epsilon_b-W^T\delta_a$

而 $S=U^*-WV^{*-1}W^T$ 称为简化摄像机矩阵。

三、稀疏BA迭代步长的算法求解过程

算法输入：

m个初始相机参数 $a_j$ ，j=1,...,m;n个初始三维物点坐标 $b_i$ ,i=1,...,n,观测的特征点坐标 $x_i_j$ ,LM算法的阻尼因子μ。

算法输出：

基于LM的稀疏BA迭代步长的解

算法流程：

计算偏导数矩阵，Q表示投影函数，i=1,...,n,j=1...,m

$A_i_j=\frac{\partial X_i_j^{'}}{\partial a_j}=\frac{\partial Q(a_j,b_i)}{\partial a_j}$

$B_i_j=\frac{\partial X_i_j^{'}}{\partial b_i}=\frac{\partial Q(a_j,b_i)}{\partial b_i}$

计算残差：

$\epsilon_i_j=X_i_j-X_i_j^{'}$

计算辅助变量：

$U_j=\sum_{i}A_i_j^TA_i_j\quad V_i=\sum_{j}B_i_j^TB_i_j\quad W_i_j=A_i_j^TB_i_j$

$\epsilon_{a_j}=\sum_{i}A_i_j^T\epsilon_i_j\quad \epsilon_{b_i}=\sum_{j}B_i_j^T\epsilon_i_j$

将Uj和Vide主对角线元素上加上阻尼因子μ，得到Uj*和Vi*。

计算： $Y_i_j=W_i_jV_i^{*-1}$

对于 $\delta_a$ ：

$S(\delta_{a_1}^T,\delta_{a_2}^T,...,\delta_{a_m}^T)^T=(e_1^T,e_2^T,...,e_m^T)^T$ ，S是由多个m*m分块构成的矩阵

$S_j_k=\delta_j_kU_j^*-\sum_{i}Y_i_jW_i_k^T$

$\delta_j_k=\left\{\begin{matrix} 0\quad ,j\n\neq k \\ 1\quad ,j=k \end{matrix}\right.$

$e_j=\epsilon_{a_j}-\sum_{i}Y_i_j\epsilon_{b_i}$

对于 $\delta_b$ ：

$\delta_{b_i}=V_i^{*-1}(\epsilon_{b_i}-\sum_{j}W_i_j^T\delta_{a_j})$

拼接 $\delta_a$ 和 $\delta_b$ ，就得到LM的迭代步长 $\delta$ 。

您可能感兴趣的与本文相关的镜像

Python3.10

Conda

Python

Python 是一种高级、解释型、通用的编程语言，以其简洁易读的语法而闻名，适用于广泛的应用，包括Web开发、数据分析、人工智能和自动化脚本