2020-12/10---剑指offer打卡

最新推荐文章于 2025-11-23 23:25:20 发布

原创最新推荐文章于 2025-11-23 23:25:20 发布 · 186 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#数据结构 #算法

剑指offer

数组中出现超过一半的数字

题目描述

数组中有一个数字出现的次数超过数组长度的一半，请找出这个数字。例如输入一个长度为9的数组{1,2,3,2,2,2,5,4,2}。由于数字2在数组中出现了5次，超过数组长度的一半，因此输出2。如果不存在则输出0。

解题思路

1.哈希表：统计每个数出现的次数；时间复杂度O(n),空间复杂度O（N);
2.排序法：先将数组排序，可能的众数肯定在数组中间，然后判断一下，排序时的时间复杂度为O（nlogn),空间复杂度为O(1）；
3.相互抵消算法：首先定义出现的次数cnt为1，初始值为val,如果后面一个数字和相面不同则相减，同时更新val;相同则相加，如果存在大于一半的众数那么一定是最后的val,但最后要加个循环判断是否真的满足条件。时间复杂度为O（N),空间复杂度O(1）；
4.暴力解法：遍历数组，统计每个数出现的次数，时间复杂度O(n^2)

代码实现

class Solution {
public:
    int MoreThanHalfNum_Solution(vector<int> numbers) {
        /*思路一：数组排序后，如果符合条件的数存在，则一定是数组中间那个数
        int len=numbers.size();
        sort(numbers.begin(),numbers.end());
        int mid=numbers[len/2];
        int cnt=0;
        for(int i=0;i<len;i++){
            if(numbers[i]==mid) cnt++;
        }
        return cnt>len/2?mid:0;*/
        //思路2：相互抵消算法
        /*if(numbers.empty()) return 0;
        int res=numbers[0];
        int cnt=1;//统计次数
        for(int i=1;i<numbers.size();i++){
            if(numbers[i]==res){
                cnt++;
            }else{
                cnt--;
                if(cnt==0){
                    res=numbers[i];
                    cnt=1;
                }
            }
        }
        //如果存在大于一半的数要么有相邻的，要么是最后一位（如12121）
        //12345666，最后是6但次数不大于一半，所以最后要加个判断
        int num=0;
        for(int i=0;i<numbers.size();i++){
            if(numbers[i]==res){
                num++;
            }
        }
        return num>numbers.size()/2?res:0;*/
        //思路3：哈希表
        /*map<int,int>mp;
        for(int i=0;i<numbers.size();i++){
            ++mp[numbers[i]];
            if(mp[numbers[i]]>numbers.size()/2)
                return numbers[i];
        }
        return 0;*/
        //思路4：暴力解法
        int half=numbers.size()/2;
        for(int i=0;i<numbers.size();i++){
            int cnt=1;
            int num=numbers[i];
            for(int j=i+1;j<numbers.size();j++){
                if(num==numbers[j]){
                    cnt++;
                }
            }
            if(cnt>half){
                return num;
            }
        }
        return 0;
       }
};

题目描述

求出1~13的整数中1出现的次数,并算出100~1300的整数中1出现的次数？为此他特别数了一下1~13中包含1的数字有1、10、11、12、13因此共出现6次,但是对于后面问题他就没辙了。ACMer希望你们帮帮他,并把问题更加普遍化,可以很快的求出任意非负整数区间中1出现的次数（从1 到 n 中1出现的次数）。

解题思路：
转自：题解
根据当前位cur值的不同，分为以下三种情乱：

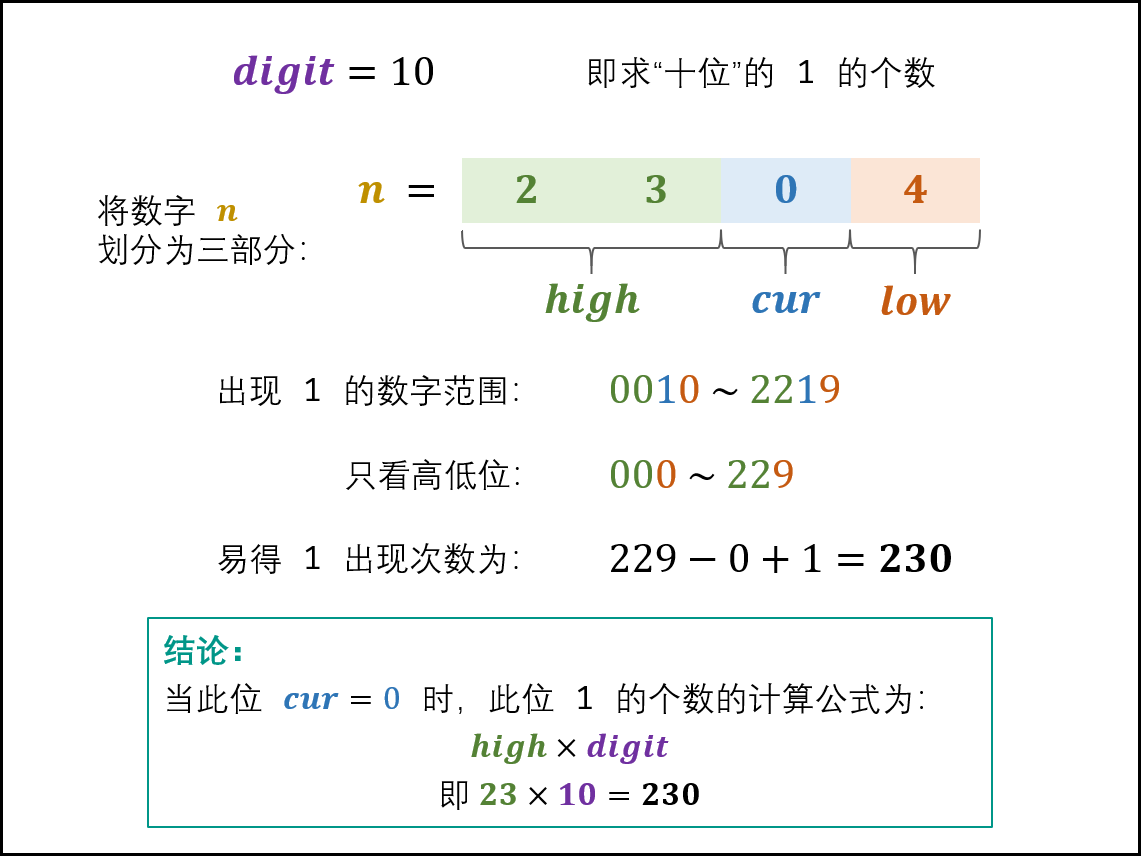
1、当 cur=0 时：此位 11 的出现次数只由高位 high 决定，计算公式为：high*digit;

2、当 cur = 1cur=1 时：此位 11 的出现次数由高位 highhigh 和低位 lowlow 决定，计算公式为：
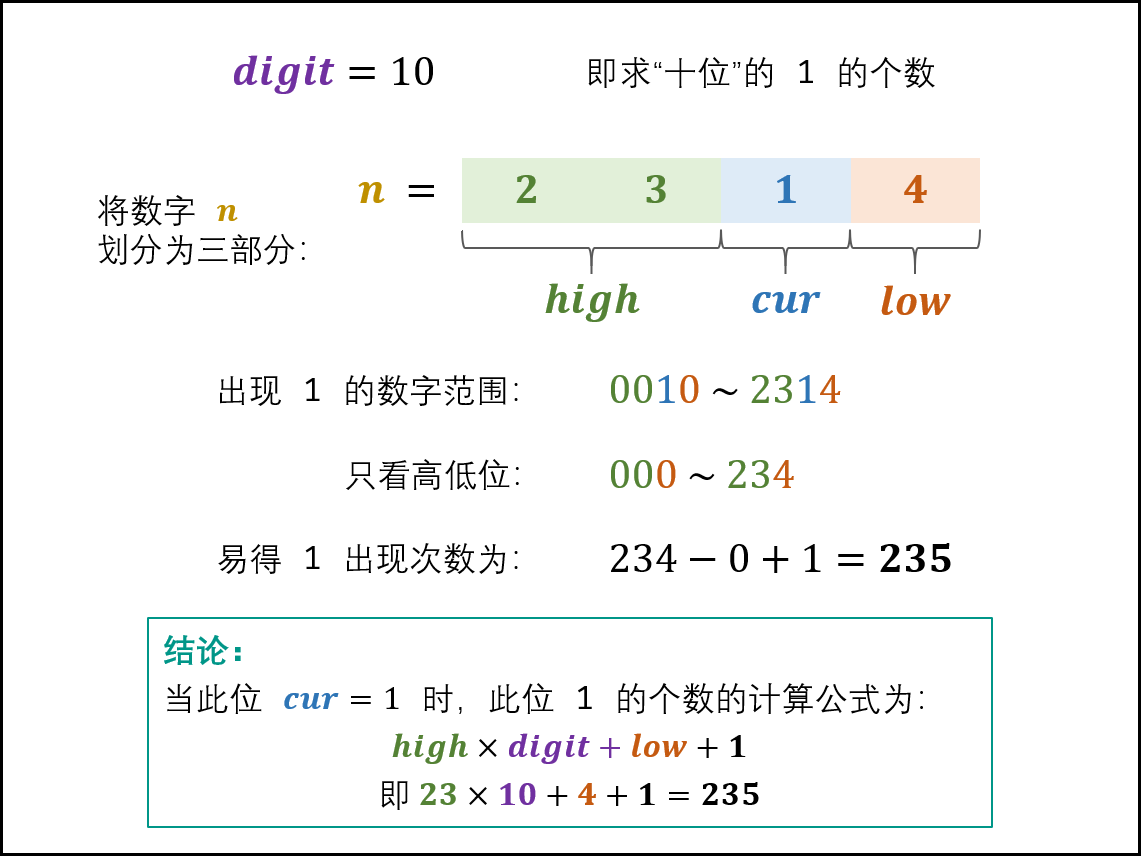
在这里插入图片描述
3、当 cur = 2, 3, …, 9 时：此位 11 的出现次数只由高位 high 决定，计算公式为：

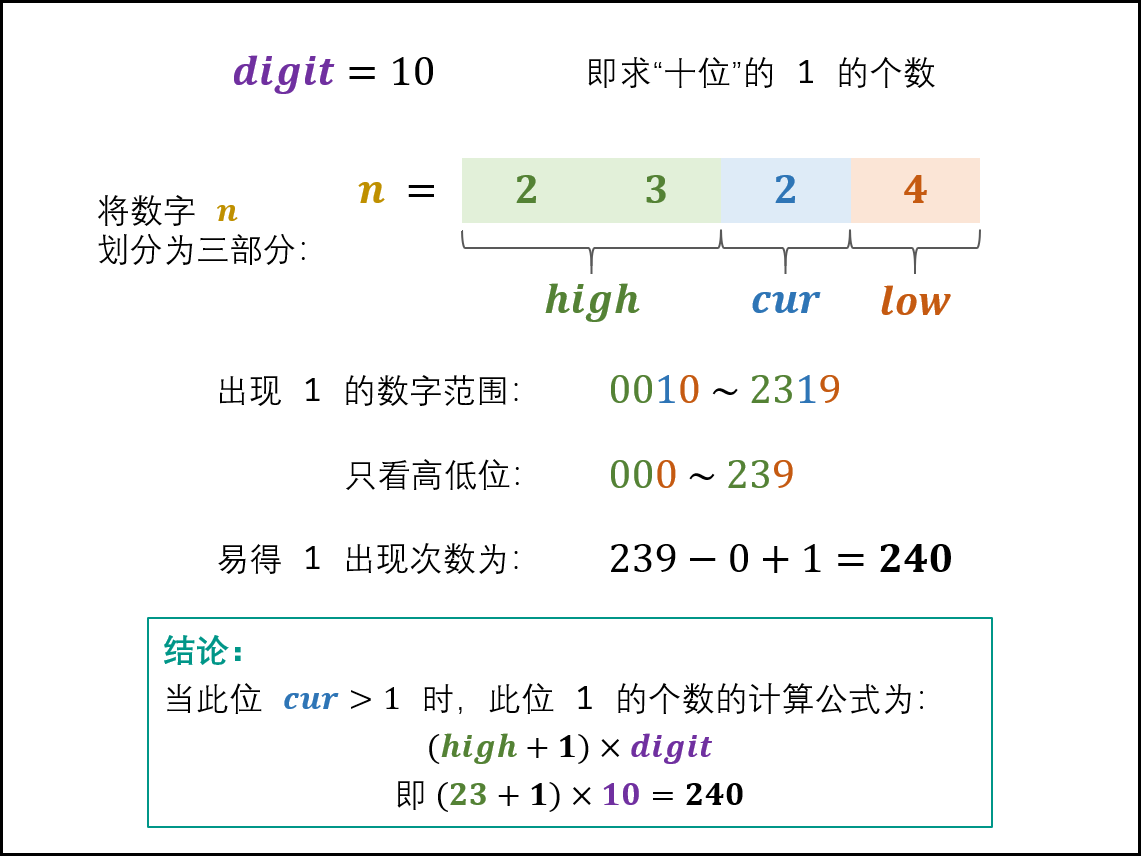
class Solution {
    int countDigitOne(int n) {
        long digit = 1, res = 0;
        long high = n / 10, cur = n % 10, low = 0;
        while(high != 0 || cur != 0) {
            if(cur == 0) res += high * digit;
            else if(cur == 1) res += high * digit + low + 1;
            else res += (high + 1) * digit;
            low += cur * digit;
            cur = high % 10;
            high /= 10;
            digit *= 10;
        }
        return res;
    }
}

把数组排成最小的数

题目描述

输入一个正整数数组，把数组里所有数字拼接起来排成一个数，打印能拼接出的所有数字中最小的一个。例如输入数组{3，32，321}，则打印出这三个数字能排成的最小数字为321323。

class Solution {
public:
    //仿函数，自定义排序
    static bool cmp(int a,int b){
        string A=to_string(a)+to_string(b);
        string B=to_string(b)+to_string(a);
        return A<B;
    }
    string PrintMinNumber(vector<int> numbers) {
        if(numbers.size()==0) return "";
        sort(numbers.begin(),numbers.end(),cmp);
        string res="";
        for(int i=0;i<numbers.size();i++){
            res+=to_string(numbers[i]);
        }
        return res;
    }
};

丑数

题目描述

把只包含质因子2、3和5的数称作丑数（Ugly Number）。例如6、8都是丑数，但14不是，因为它包含质因子7。
习惯上我们把1当做是第一个丑数。求按从小到大的顺序的第N个丑数

常规判断是否是丑数：

    bool isugly(int num){
        while(num%2==0){
            num/=2;
        }
        while(num%3==0){
            num/=3;
        }
        while(num%5==0){
            num/=5;
        }
        return num==1?true:false;
    }

解题思路：

假设当前存在 3 个数组 nums2, nums3, nums5 分别代表丑数序列从 1 开始分别乘以 2, 3, 5 的序列，即{1,2,3,5,6,8…}分别乘以2，3，5：

nums2 = {1*2, 2*2, 3*2, 4*2, 5*2, 6*2, 8*2…}
nums3 = {1*3, 2*3, 3*3, 4*3, 5*3, 6*3, 8*3…}
nums5 = {1*5, 2*5, 3*5, 4*5, 5*5, 6*5, 8*5…}
最终的丑数序列实际上就是这 3 个有序序列对的合并结果，计算丑数序列也就是相当于合并 3 个有序序列。

合并 3 个有序序列，最简单的方法就是每一个序列都各自维护一个指针，然后比较指针指向的元素的值，将最小的放入最终的合并数组中，
并将相应指针向后移动一个元素。这也就是：

for(int i=1;i<index;i++){
            res[i]=min(res[p2]*2,min(res[p3]*3,res[p5]*5));
            if(res[i]==res[p2]*2) p2++;
            if(res[i]==res[p3]*3) p3++;
            if(res[i]==res[p5]*5) p5++;
        }

nums2, nums3, nums5 中是存在重复的解的，例如 nums2[2] == 3*2, nums3[1] == 2*3 都计算出了 6 这个结果，所以在合并 3 个有序数组的过程中，还需要跳过相同的结果，这也就是为什么在比较的时候，需使用 3 个并列的 if… if… if… 而不是 if… else if… else 这种结构的原因。当比较到元素 6 时， if (res[i] == res[p2] * 2)…if (res[i] == res[p3] * 3)… 可以同时指向 nums2, nums3 中元素 6 的下一个元素.

class Solution {
public:
    int GetUglyNumber_Solution(int index) {
        if(index<=0) return 0;
        int p2=0,p3=0,p5=0;//初始化三个指向三个潜在成为最小丑数的地址
        int *res=new int[index];
        res[0]=1;
        for(int i=1;i<index;i++){
            res[i]=min(res[p2]*2,min(res[p3]*3,res[p5]*5));
            if(res[i]==res[p2]*2) p2++;
            if(res[i]==res[p3]*3) p3++;
            if(res[i]==res[p5]*5) p5++;
        }
        return res[index-1];
    }
};

第一个只出现一次的字符

题目描述

在一个字符串(0<=字符串长度<=10000，全部由字母组成)中找到第一个只出现一次的字符,并返回它的位置, 如果没有则返回
-1（需要区分大小写）.（从0开始计数）

解题思路：

利用哈希表，统计每个字符出现的次数即可

class Solution {
public:
    int FirstNotRepeatingChar(string str) {
        if(str.size()==0) return -1;
        map<char,int>mp;
        for(int i=0;i<str.size();i++){
            ++mp[str[i]];
        }
        for(int j=0;j<str.size();j++){
            if(mp[str[j]]==1)
                return j;
        }
        return -1;
    }
};

数组中的逆序对

题目描述

在数组中的两个数字，如果前面一个数字大于后面的数字，则这两个数字组成一个逆序对。输入一个数组,求出这个数组中的逆序对的总数P。并将P对1000000007取模的结果输出。
即输出P%1000000007

解题思路:

利用归并排序时间复杂度为O(nlongn)

class Solution {
public:
    const int kmod=1000000007;
    void merge_(vector<int>&arr,vector<int>&tmp,int l,int mid,int r,int &res){
        int i=l,j=mid+1,k=0;
        while(i<=mid&&j<=r){
            //加上等于之后是稳定排序，否则不是
            if(arr[i]>=arr[j]){
                tmp[k++]=arr[j++];
                res+=(mid-i+1);
                res%=kmod;
            }else{
                tmp[k++]=arr[i++];
            }
        }
        while(i<=mid){
            tmp[k++]=arr[i++];
        }
        while(j<=r){
            tmp[k++]=arr[j++];
        }
        for(i=l,k=0;i<=r;i++,k++){
            arr[i]=tmp[k];
        }
    }
    void merge_sort(vector<int>&arr,vector<int>&tmp,int l,int r,int &res){
        if(l>=r){
            return ;
        }
        int mid=l+((r-l)>>1);
        merge_sort(arr,tmp,l,mid,res);
        merge_sort(arr,tmp,mid+1,r,res);
        merge_(arr,tmp,l,mid,r,res);
    }
    int InversePairs(vector<int> data) {
        if(data.size()==0) return 0;
        vector<int>tmp(data.size());
        int res=0;
        merge_sort(data,tmp,0,data.size()-1,res);
        return res;
    }
};