2020/12/08----剑指offer打卡

最新推荐文章于 2024-08-24 12:44:53 发布

原创最新推荐文章于 2024-08-24 12:44:53 发布 · 153 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#二叉树 #链表 #指针 #数据结构

21.栈的压入、弹出序列

题目描述

输入两个整数序列，第一个序列表示栈的压入顺序，请判断第二个序列是否可能为该栈的弹出顺序。假设压入栈的所有数字均不相等。例如序列1,2,3,4,5是某栈的压入顺序，序列4,5,3,2,1是该压栈序列对应的一个弹出序列，但4,3,5,1,2就不可能是该压栈序列的弹出序列。（注意：这两个序列的长度是相等的）

解题思路：

构造一个辅助的栈，每次入栈之后与弹出栈的元素依次从序号为0的元素比较，相等则弹出，如果最后辅助栈为空，说明是一个弹出序列，否则不是。

代码实现：

class Solution {
public:
    bool IsPopOrder(vector<int> pushV,vector<int> popV) {
        int n=pushV.size();
        int j=0;
        stack<int>temp;
        for(int i=0;i<n;i++){
            temp.push(pushV[i]);
            
            while(!temp.empty()&&temp.top()==popV[j]){
                temp.pop();
                j++;
            }
        }
        return temp.empty();
    }
};

22.从上到下打印二叉树（树的层序遍历）

题目描述

从上往下打印出二叉树的每个节点，同层节点从左至右打印。

解题思路：层次遍历

初始化：一个队列queue<TreeNode*> q，将root节点入队列q
如果队列不空，做如下操作：
弹出队列头，保存为node，将node的左右非空孩子加入队列
做2,3步骤，知道队列为空

如果不需要确定当前遍历到了哪一层，模板如下：

void bfs() {
    vis[] = 0;//标记数组
    queue<int> pq(start_val);

    while (!pq.empty()) {
        int cur = pq.front(); 
        pq.pop();
        for (遍历cur所有的相邻节点nex) {
            if (nex节点有效 && vis[nex]==0){
                vis[nex] = 1;//节点以访问
                pq.push(nex)
            }
        }
    }
}

如果需要确定遍历到哪一层，模板如下：

void bfs() {
    int level = 0;//表示遍历的层数
    vis[] = 0; // or set
    queue<int> pq(original_val);
    while (!pq.empty()) {
        int sz = pq.size();//记录每一层的元数个数
        while (sz--) {
                int cur = pq.front(); pq.pop();
            for (遍历cur所有的相邻节点nex) {
                if (nex节点有效 && vis[nex] == 0) {
                    vis[nex] = 1;
                    pq.push(nex)
                }
            } // end for
        } // end inner while
        level++;

    } // end outer while
}

代码实现：

/*
struct TreeNode {
	int val;
	struct TreeNode *left;
	struct TreeNode *right;
	TreeNode(int x) :
			val(x), left(NULL), right(NULL) {
	}
};*/
class Solution {
public:
    vector<int> PrintFromTopToBottom(TreeNode* root) {
        queue<TreeNode*>que;
        vector<int>ans;
        if(root==nullptr) return ans;
        que.push(root);
        while(!que.empty()){
            int sz=que.size();
            while(sz--){
                TreeNode *tmp=que.front();
                que.pop();
                ans.push_back(tmp->val);
                if(tmp->left)  que.push(tmp->left);
                if(tmp->right) que.push(tmp->right);
            }
        }
        return ans;

    }
};

23、二叉搜索树的后序遍历序列

题目描述

输入一个整数数组，判断该数组是不是某二叉搜索树的后序遍历的结果。如果是则返回true,否则返回false。假设输入的数组的任意两个数字都互不相同。

什么是二叉搜索树：

二叉搜索树(Binary Search Tree)，又名二叉排序树(Binary Sort Tree)。
二叉搜索树是具有有以下性质的二叉树：
（1）若左子树不为空，则左子树上所有节点的值均小于或等于它的根节点的值。
（2）若右子树不为空，则右子树上所有节点的值均大于或等于它的根节点值
（3）左、右子树也分别为二叉搜索树。

解题思路：

后序遍历的最后一个数一定是根节点，而根据二叉搜索树的性质，左子树的值一定小于根节点的值，右节点的值一定大于根节点的值，所以在数组中找到比节点大的第一个数即可把原数组分为左右两部分。然后递归判断左右子树即可，注意递归的边界条件为l大于等于r，l等于r会出错，l大于R也可也执行。
**

代码实现：

class Solution {
public:
    bool vf(vector<int> &sequence,int l,int r){
        //边界条件大于等于最为关键
        if(l>=r) return true;
        int i=0;
        for(i=l;i<r;i++){
            if(sequence[i]>sequence[r])
                break;
        }
        for(int j=i;j<r;j++){//如果右边小于根节点直接return false;
            if(sequence[j]<sequence[r])
                return false;
        }
        return vf(sequence,l,i-1)&&vf(sequence,i,r-1);
    }
    bool VerifySquenceOfBST(vector<int> sequence) {
        if(sequence.size() == 0) return  false;
        return vf(sequence,0,sequence.size()-1);
    }
};

25、复杂链表的复制

题目描述

输入一个复杂链表（每个节点中有节点值，以及两个指针，一个指向下一个节点，另一个特殊指针random指向一个随机节点），请对此链表进行深拷贝，并返回拷贝后的头结点。（注意，输出结果中请不要返回参数中的节点引用，否则判题程序会直接返回空）

解题思路：
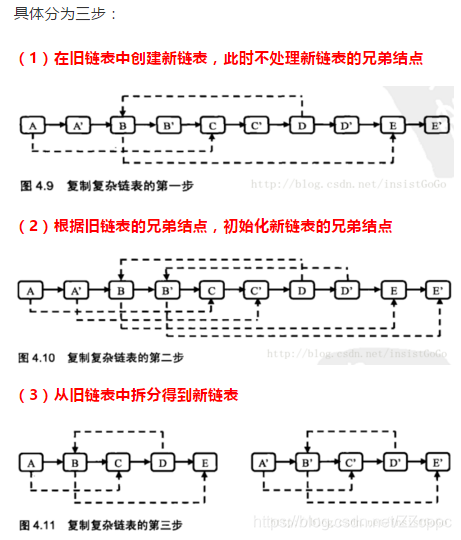
在这里插入图片描述
代码实现：

/*
struct RandomListNode {
    int label;
    struct RandomListNode *next, *random;
    RandomListNode(int x) :
            label(x), next(NULL), random(NULL) {
    }
};
*/
class Solution {
public:
    //第一步，复制每一个节点，如复制节点A得到A1,将A1插入到节点A的后面
    void CloneNodes(RandomListNode *pHead){
        RandomListNode *pNode=pHead;
        while(pNode){
            RandomListNode *pcloned=new RandomListNode(pNode->label);
            pcloned->next=pNode->next;
            pcloned->random=nullptr;
            pNode->next=pcloned;
            pNode=pcloned->next;
            
        }
    }
    //第二步，为复制出来的节点添加random节点。A1->random=A->random->next;
    void ConnectNodes(RandomListNode *pHead){
        RandomListNode *pNode=pHead;
        while(pNode){
            RandomListNode *pcloned=pNode->next;
            if(pNode->random!=nullptr){
                pcloned->random=pNode->random->next;
            }
            pNode=pcloned->next;
        }
    }
    //第三步：将链表拆分成原链表和复制后的链表
    RandomListNode *Reconnect(RandomListNode *pHead){
       RandomListNode *pclonedhead=pHead->next;
        RandomListNode *pNode=pHead;
        while(pNode){
            RandomListNode *clonednode=pNode->next;
            pNode->next=clonednode->next;
            clonednode->next=clonednode->next==nullptr?nullptr:clonednode->next->next;
            pNode=pNode->next;
        }
        return pclonedhead;
    }
    
    RandomListNode* Clone(RandomListNode* pHead)
    {
        if(!pHead) return nullptr;
        CloneNodes(pHead);
        ConnectNodes(pHead);
        return Reconnect(pHead);
        
    }
};

24. 二叉树中和为某一值的路径

题目描述

输入一颗二叉树的根节点和一个整数，按字典序打印出二叉树中结点值的和为输入整数的所有路径。路径定义为从树的根结点开始往下一直到叶结点所经过的结点形成一条路径。

前置知识：

1.叶子节点表示：如果节点为root，那么当前节点为叶子节点的必要条件为!root->left && !root->right
2.找出路径，当然需要遍历整棵树，这里采用先序遍历，即：根节点，左子树，右子树

递归算法三部曲：

1.明白递归函数的功能：FindPath(TreeNode* root,int sum)，从root节点出发，找和为sum的路径
2. 递归终止条件：当root节点为叶子节点并且sum==root->val, 表示找到了一条符合条件的路径
3.下一次递归：如果左子树不空，递归左子树FindPath(root->left, sum - root->val),如果右子树不空，递归右子树，FindPath(root->right, sum - root->val)

可以用两个全局变量vector<int> path, vector<vector<int>> ret来保存
代码中用了引用，将全局变量作为函数参数来进行全局传递。

代码实现

/*
struct TreeNode {
	int val;
	struct TreeNode *left;
	struct TreeNode *right;
	TreeNode(int x) :
			val(x), left(NULL), right(NULL) {
	}
};*/
class Solution {
public:
    vector<vector<int>>ret;
    vector<int>path;
    void dfs(TreeNode *root,int sum,vector<int>&path,vector<vector<int>>&ret){
        path.push_back(root->val);
        if(sum==root->val&&!root->left&&!root->right){
            ret.push_back(path);
        }
        if(root->left) dfs(root->left,sum-root->val,path,ret);
        if(root->right) dfs(root->right,sum-root->val,path,ret);
        path.pop_back();//回溯,重要.代表当前path中的root节点我已经不需要了
    }
    vector<vector<int> > FindPath(TreeNode* root,int expectNumber) {
        if(root==nullptr) return ret;
        dfs(root,expectNumber,path,ret);
        return ret;
    }
};

注意：

上面的回溯过程相当于一个深度优先遍历的过程，每次访问完叶子节点之后回溯到上一层，直到所有的叶子节点都被访问完为止。

26.二叉搜索树与双向链表

题目描述

输入一棵二叉搜索树，将该二叉搜索树转换成一个排序的双向链表。要求不能创建任何新的结点，只能调整树中结点指针的指向。

解题思路：

不是很懂。。

代码实现

/*
struct TreeNode {
	int val;
	struct TreeNode *left;
	struct TreeNode *right;
	TreeNode(int x) :
			val(x), left(NULL), right(NULL) {
	}
};*/
class Solution {
public:
    //**注意此处一定要用引用**
    void inorder(TreeNode *pRoot,TreeNode *&pre){
        if(pRoot==nullptr) return ;
        inorder(pRoot->left,pre);
        if(pre!=NULL){
            pRoot->left=pre;
            pre->right=pRoot;
        }
        pre=pRoot;
        inorder(pRoot->right,pre);
    }
    TreeNode* Convert(TreeNode* pRootOfTree)
    {
        if(pRootOfTree==nullptr) return nullptr;
        TreeNode *pre=NULL;
        inorder(pRootOfTree,pre);
        while(pre->left!=NULL)
            pre=pre->left;
        return pre;
        
    }
};