python递归以及c语言递归实现求最大公约数（补充上文）_m=input("m=") n=input("n=") if m

本文链接：https://blog.youkuaiyun.com/ZZRBlogger/article/details/121613402

本文介绍了如何使用Python和C语言实现欧几里得算法（辗转相除法）来求最大公约数，并通过递归方式展示。在Python中，还涉及了递归计算斐波那契数列和汉诺塔游戏的解决方案。代码清晰易懂，适合初学者理解递归在不同语言中的应用。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

前面已经写过了欧几里得算法（即辗转相除法）c语言的写法，今天用python和c的递归来实现辗转相除法

需注意：python代码中当输入999和991时，会造成互质现象

##输入M和N
M = int(input())
N = int(input())
M1 = M
N1 = N
if M < N:
    M , N = N , M  //比较M N大小并进行交换
R = M % N
while R != 0:
    M = N
    N = R
    R = M % N
if N !=1:
    print('%d和%d的最大公约数为%d。' %(M1,N1,N))
else:
    print('%d与%d互质。' %(M1,N1))

c语言中是如和实现的呢：

#include <stdio.h>
void Swap(int x, int y)
{
	int z = 0;
	z = x;
	x = y; 
	y = z;
}
int gcd(int x,int y)
{
	if(y>x)
	{
		Swap(x,y);
	}
	if(x % y == 0)
	{
		return y;
	}
	else
		return gcd(y,x%y);	
}
int main()
{
	int m ,n;
	scanf("%d %d",&m,&n);
	printf("最大公约数为%d",gcd(m,n));
	return 0;
}

由于c语言和python语言的区别，不能直接进行数值交换，因此在此处又重新定义了判断大小并交换的函数---

本周python递归其他题目：
利用递归实现斐波那契数列的计算：

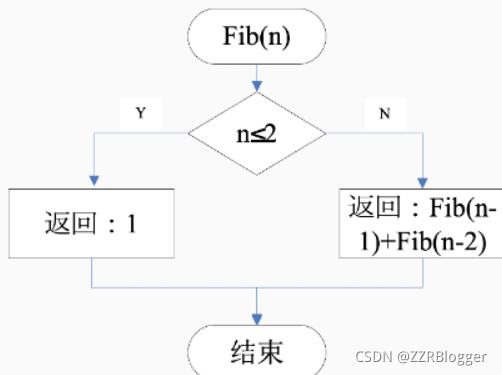
Fibonacci数列的递归算法输入：正整数n 输出：Fibonacci数列的第n项 Fib(n)
1 IF n≤2 2 THEN RETURN 1
3 RETURN Fib(n-1) + Fib(n-2) //self call

def fab(n):
    if n <= 2:
        return 1
    else:
        return fab(n-1) + fab(n-2)
             
    
if(__name__=="__main__"):
    global result
    n_str = input('请输入需要计算fabonacci数列的第几个元素：')
    n = int(n_str)
    result=fab(n)
    print(result)

汉诺塔游戏：
此代码可实现每一步的操作过程以及操作总次数：

def Hanoi(n, A, C, B):
    global count
    if n <1:
        print('invalid input')
    elif n == 1:
        print("%d:\t%s ---> %s" %(count,A,C))
        count = count +1
    else:
        Hanoi(n-1,A,B,C)
        Hanoi(1,A,C,B)
        Hanoi(n - 1,B,C,A)
    
if(__name__ == "__main__"):
    count = 1
    n = int(input('请输入A柱子上的圆盘个数：'))
    Hanoi(n,'A','C','B')

有问题请指教！