A 1049 Counting Ones (30分)

							A 1049 Counting Ones (30分)

这道题目我看到后根本没有任何思路，没办法只好一个个数枚举，然后暴力破解，但只通过了部分测试点，想了好久，都没有过，最后去看的《算法笔记》，才看懂了这道题.这道题我感觉要我自己做的话，我估计到死都不会AC的.毕竟太菜了.
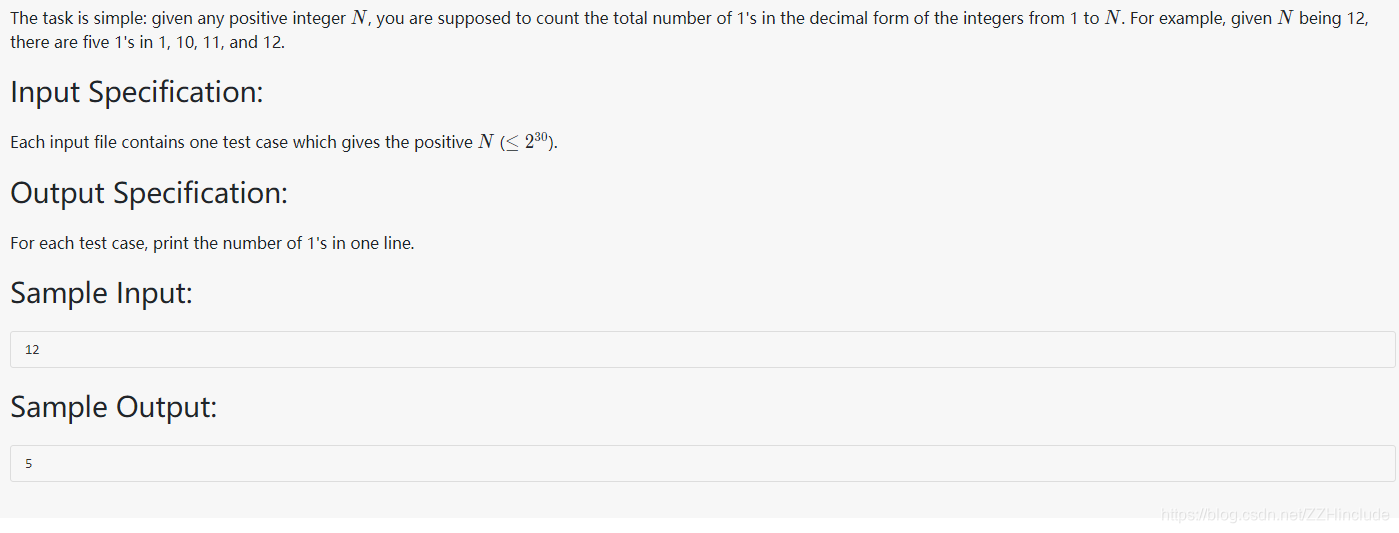
**题目大意：**首先给你一个数，然后让你判断从0到这个数中共有多少个1.
举一个例子来分析 48210这个数字，
（下列说的左边 右边都是相对于当前的位数所说的）
①从个位数开始，当个位数是1的时候，那么它左边的位数就只能是0000-4820，不能是0000-4821 因为此时个位数是1，那么数字就变成了42811>48210，所以此时有4821个1；
②十位上是1的时候，此时十位的左边是482，右边是0，先分析从 000-481，个位数可以任意取（0-9），因为 0001X - 4811X都小于48210，然后分析4821X，得出X只能取0，否则超出范围，所以此时有482*10+1 = 4821；
③百位上是1的时候，左边的数是48，右边的数是10，因为48210百位上的数字是2大于1，所以左边可以取00-48，右边的数字可以取00-99，,001XX - 481XX都不会超过范围，所以此时有（48+1）100 = 4900；
④千位上是1的时候，左边的数4，右边的数是210，因为8大于1，所以左边的数0-4任意取，右边的数000-999任意取，01XXX-41XXX都不会超范围，所以此时有 （4+1） 1000 = 5000；
⑤万位上是1的时候，即1XXXX ，所以是 0000 - 9999；此时有10000个数字1；
所以最后的结果 SUM = 4821 + 4821 + 4900 + 5000 + 10000 = 29542

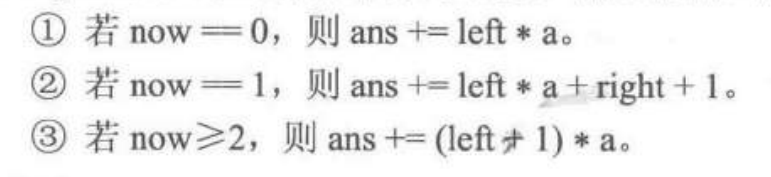
#include <stdio.h>

int main(void)
{
    int left,now,right;
    int num;
    int a = 1;
    int sum = 0;
    scanf("%d",&num);

    while(num / a)
    {
        left = num / (a * 10);
        now = num / a % 10;
        right = num % a;
        if(now == 0) sum += left * a;
        else if(now == 1) sum += left * a + 1 + right;
        else sum += (left + 1) * a;
        a *= 10;
    }

    printf("%d\n",sum);
    return 0;
}

写完后又到了该睡觉的时候了，明天继续冲！