基于 Python 实现 MODIS NDVI 逐年数据的 MK 趋势检验

目录

1 Mann-Kendall趋势检验算法

1.1 基本概念

1.2 具体原理

1.3 计算步骤

2 Python环境配置

3 Python完整代码

4 Python代码运行结果

---

1 Mann-Kendall趋势检验算法

1.1 基本概念

Mann-Kendall检验是一种非参数检验（无分布检验），用于检测时间序列数据中的单调趋势，不受数据分布限制，其优点是不要求样本遵从一定的分布，也不受少数异常值的干扰。该方法由Mann(1945)提出，后经Kendall(1975)完善，基于秩次比较原理，通过计算数据序列中所有可能配对的差值符号，得出趋势统计量及其显著性水平。常用于对降水、径流、气温和水质等要素时间序列变化趋势和突变点分析。

Mann-Kendall非参数检验方法常用于水质、径流量、温度、降水等水文气象时间序列变化趋势的显著性检验。该方法不需要测量值服从正太分布，不受缺失值和异常值的影响。在遥感中，MK趋势检验常用于分析植被指数(如NDVI、EVI)的长时间序列变化，帮助研究者识别植被覆盖变化的方向、速率及显著性水平，为生态环境监测、气候变化研究提供科学依据。

趋势分析可用于各种应用，例如水文学、气候学、城市测绘、农作物监测等，Mann-Kendall (MK) 趋势检验和 Sen 的斜率估计等非参数方法能够提供时间和空间尺度数据的趋势及其显著性水平。

Mann-Kendall检验的假设：原假设——时间序列中不存在趋势变化，备择假设——时间序列中存在趋势变化。其基本思想是通过比较每对数据点之间的大小关系来检查序列中的趋势，然后根据秩和的正负性来确定趋势的方向。

1.2 具体原理

对任意待检序列Xt(t=1,2,…,n)，n为待检序列长度，可定义统计量S：

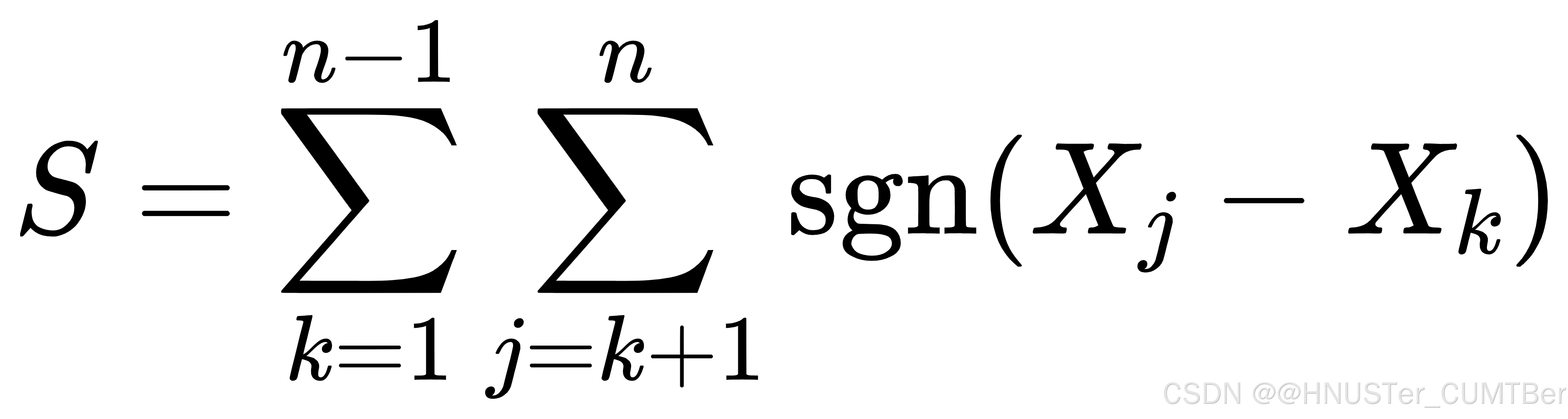
其中：Xj和Xk为时间序列相应年份数据；n为时间序列长度；sgn(Xj-Xk)为符号函数。

当Xj＞Xk时，sgn值为1；当Xj＜Xk时，sgn值为-1；当Xj＝Xk时，sgn值为0。 

当n≥10时，统计量S近似服从正态分布，其期望和方差分别为： 

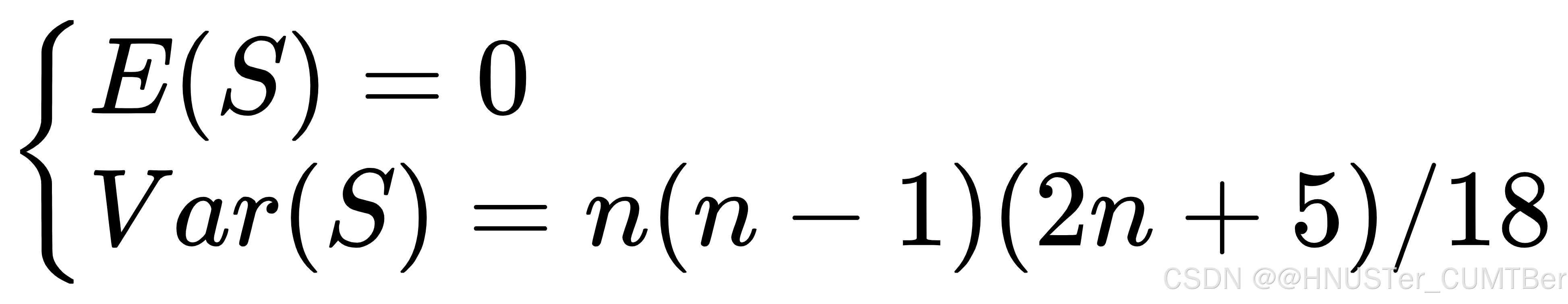
按照下式可构造标准化的检验统计量Z：

Z服从标准正态分布，当Z>0时，存在上升的趋势；当Z<0时，存在下降的趋势。对于给定的显著性水平α，如果|Z|≥Z1-α/2，说明时间序列存在显著向上或向下的趋势。

当|Z|≥1.64、1.96、2.58时则说明该时间序列分别通过了置信水平90%、95%、99%的显著性检验。