二叉树中和为某一值的路径

问题

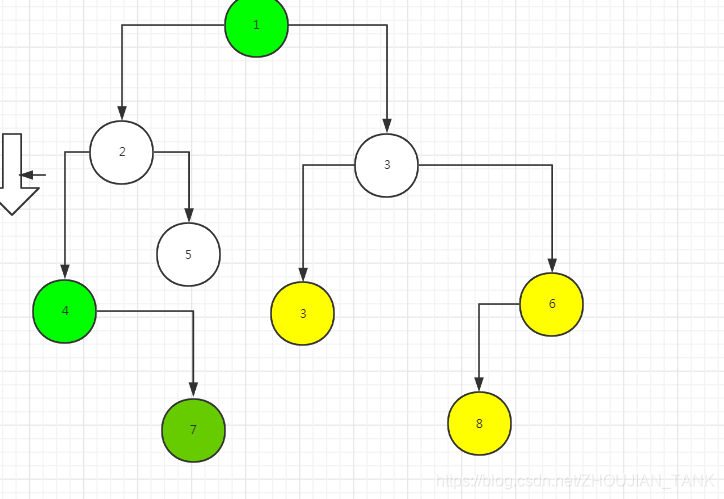
输入一颗二叉树的根节点和一个整数，打印出二叉树中结点值的和为输入整数的所有路径。路径定义为从树的根结点开始往下一直到叶结点所经过的结点形成一条路径。(注意: 在返回值的list中，数组长度大的数组靠前)

分析

注意叶子节点是既没有左子树也没有右子树
还是用到低估与遍历左右子树的这种策略
总结，总结

• 将root值加入到list中，同时将target值减掉root值
• 若此时target值为0并且root为叶子节点则表明这是一条路径，返回
• 递归左子树
• 递归右子树
• 取出list中的value进行回到父节点
• 返回

代码

package DlinkedList;

import java.util.ArrayList;

/**
 * @Author Zhou  jian
 * @Date 2020 ${month}  2020/3/22 0022  14:12
 * 输入一颗二叉树的根节点和一个整数，
 * 打印出二叉树中结点值的和为输入整数的所有路径。
 * 路径定义为从树的根结点开始往下一直到叶结点所经过的结点形成一条路径。
 * (注意: 在返回值的list中，数组长度大的数组靠前)
 */
public class Problem11 {


    //定义返回的值
    private ArrayList<ArrayList<Integer>> listAll = new ArrayList<ArrayList<Integer>>();


    private ArrayList<Integer> list = new ArrayList<Integer>();

    public ArrayList<ArrayList<Integer>> FindPath(TreeNode root,int target) {

        //遍历到叶子节点则返回
        if(root == null) return listAll;


        //将当前值加入到list中
        list.add(root.val);

        //将待比较的值减去跟节点的值
        target -= root.val;

        //假如遍历到叶子节点并且target值刚好为0，则说明这条路径遍历完值行灯
        if(target == 0 && root.left == null && root.right == null)
            listAll.add(new ArrayList<Integer>(list));

        //查找左子树
        FindPath(root.left, target);

        //查找由子树
        FindPath(root.right, target);

        //移除最后一个元素啊，深度遍历完一条路径后要回退
        //递归到叶子节点如果还没有找到路径，就要回退到父节点继续寻找，依次类推
        list.remove(list.size()-1);


        return listAll;
    }


    //获取所有路径
//    public  ArrayList FindAllPath(TreeNode root){
//
//        //每次遍历的数据
//        ArrayList<Integer> arrayList = new ArrayList<>();
//
//        //遍历到叶子节点
//        if(root==null){
//           allpath.add(arrayList);
//        }
//
//        if(root.left!=null){
//            arrayList.add(root.val);
//            arrayList.addAll(FindAllPath(root.left));
//        }
//
//        if(root.right!=null){
//            arrayList.add(root.val);
//            arrayList.addAll(FindAllPath(root.left));
//        }
//
//
//
//   return  arrayList;
//
//
//    }



    public static void main(String[] args) {
        TreeNode A = new TreeNode(1);
        TreeNode B= new TreeNode(2);
        TreeNode C= new TreeNode(3);
        TreeNode D= new TreeNode(4);
        TreeNode E= new TreeNode(5);
        TreeNode F= new TreeNode(3);
        TreeNode G= new TreeNode(6);
        TreeNode H= new TreeNode(7);
        TreeNode I= new TreeNode(8);
        A.left=B;
        A.right=C;
        B.left=D;
        B.right=E;
        D.right=H;
        C.left=F;
        C.right=G;
        G.left=I;


        Problem11 problem11=new Problem11();

        System.out.println(problem11.FindPath(A,7));


    }

}