【双指针专题】第四讲：盛最多水的容器

原创已于 2025-10-09 09:25:09 修改 · 828 阅读

25 ·

CC 4.0 BY-SA版权

文章标签：

#算法 #c++ #leetcode

于 2025-10-04 11:00:18 首次发布

算法专题同时被 2 个专栏收录

10 篇文章

订阅专栏

双指针专题

8 篇文章

订阅专栏

🌿 从两端出发，对撞收缩，双指针进入“区间思维”新阶段。

🌱 文章摘要

前面三篇，我们分别体验了「划分型」、「反向复写型」与「快慢型」双指针。
从这一篇《盛最多水的容器》开始，我们将正式踏入 “对撞指针” 的世界。
这是一道经典到几乎人手必刷的题，它的解法不是靠蛮力，而是依赖 区间收缩 + 高度判断 的精妙策略。
理解这一题，你就真正掌握了双指针的第二大核心思想：对撞优化。

🧭 导读

欢迎来到《双指针算法专题》第四篇 👋
这是本系列的一个重要转折点，也是进入“高频面试题”的起点。

这道 《盛最多水的容器》题目本质是：

给定一个数组，每个元素代表一条竖线的高度，
你要找到两条线组成的容器能装的最大水量。

暴力法 O(n²) 很容易想到，但要在 O(n) 内完成，就必须用到“左右双指针”的智慧👇
👉 从数组两端出发，
👉 每次移动较短的一边，
👉 在收缩中不断寻找最优解。

这是我们在系列中第一次把双指针应用在“区间优化问题”上，非常关键⚡

🧭 本系列目录

📚 建议收藏此目录，方便跳转阅读

【双指针专题】第一讲：移动零-优快云博客

【双指针专题】第二讲：复写零-优快云博客

【双指针专题】第三讲：快乐数-优快云博客

【双指针专题】第四讲：盛最多水的容器-优快云博客

【双指针专题】第五讲：有效三角形的个数-优快云博客

【双指针专题】第六讲：查找总价格为目标值的两个商品-优快云博客

【双指针专题】第七讲：三数之和-优快云博客

【双指针专题】第八讲：四数之和-优快云博客

一、题目描述

给定一个长度为 n 的整数数组 height。有 n 条竖直的线，第 i 条线的两个端点分别是 (i, 0) 和 (i, height[i])。

找出其中的两条线，与 x 轴共同构成的容器，可以容纳最多的水。

说明：
你不能倾斜容器，且 n 至少为 2。

示例 1：
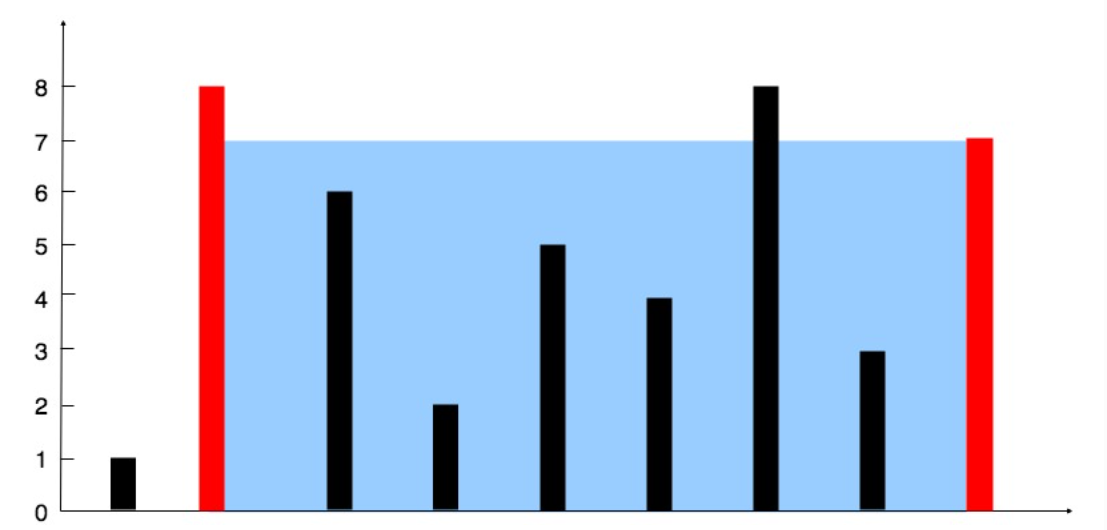
输入：[1,8,6,2,5,4,8,3,7]  
输出：49  
解释：选择第 2 条和第 9 条线（高度分别为 8 和 7），可容纳的水量为 min(8,7) * (9-2) = 7*7 = 49
示例 2：
输入：height = [1,1]  
输出：1

二、思路引导：双指针 / 对撞指针

这道题看似是一个 面积计算 问题，但直接用两层循环暴力枚举所有可能的线对，时间复杂度会达到 O(n²)，在数据量大时性能非常差。

一个更高效的办法是使用 双指针（对撞指针）：

用两个指针分别指向数组的 左右两端；
每次计算左右两端围成的面积，更新最大值；
关键技巧：每次移动高度较小的指针。

为什么要移动较小的指针？

面积由宽度与高度决定：
容量 = min(height[left], height[right]) × (right - left)
当左右指针往中间移动时，宽度会变小，为了让面积可能变大，必须让 高度变大。

如果移动较高的一边，高度不可能变大，宽度还减少，面积只会更小；

而移动较小的一边，有机会遇到更高的柱子，从而提高最小高度，弥补宽度的损失。

三、算法流程

初始化

left = 0，right = n - 1：双指针分别指向数组两端

ans = 0：记录最大面积

循环收缩

计算当前左右指针对应的容积：
h = min(height[left], height[right])
w = right - left
v = h * w
更新最大值 ans = max(ans, v)

移动较小高度的指针：

如果 height[left] < height[right] → left++

否则 right--

终止条件

当 left >= right 时，扫描完成，返回 ans。

四、代码实现（C++）

1. 暴力枚举

在讲双指针之前，我们先来看最直观的解法：暴力枚举。

思路非常直接：
枚举所有的两条线段组合；
对于每一对 (i, j)，计算其所能形成的容量：
v = min(height[i], height[j]) × (j - i)
保留所有组合中的最大值。

这种方法虽然简单，但时间复杂度为 O(n²)，当数组长度很大时，会导致超时。

下面是暴力解法的 C++ 代码：

class Solution {
public:
    int maxArea_bruteForce(vector<int>& height) {
        int n = height.size();
        int ans = 0;

        // 枚举所有可能的两条线段
        for (int i = 0; i < n; i++) {
            for (int j = i + 1; j < n; j++) {
                // 高度取两条线中较小的，宽度是两线之间的距离
                int h = min(height[i], height[j]);
                int w = j - i;
                int v = h * w;  // 容量计算
                ans = max(ans, v);
            }
        }
        return ans;
    }
};

暴力解法优点是好理解、易实现，但缺点是效率极低，在 n 较大时（如 10⁴ 级别），需要计算约 10⁸ 次，无法通过所有测试用例。

因此，我们需要更高效的解法 —— 双指针 / 对撞指针，将复杂度降低到 O(n)。

2. 对撞指针

核心逻辑如下：

每次根据左右指针计算当前容器的容量；
选择较短的一边向中间移动，尝试寻找更高的边界；
遍历一次即可完成所有可能情况的比较。

class Solution {
public:
    int maxArea(vector<int>& height) {
        int left = 0;                   // 左指针，指向数组起始位置
        int right = height.size() - 1;  // 右指针，指向数组末尾
        int ans = 0;                    // 用于记录最大容量

        while (left < right) {
            int h = min(height[left], height[right]);  // 当前容器的高度
            int w = right - left;                      // 当前容器的宽度
            int v = h * w;                             // 当前容器的容量
            ans = max(ans, v);                         // 更新最大值

            // 移动较小高度的指针，尝试找到更高的边界
            if (height[left] < height[right]) {
                left++;
            } else {
                right--;
            }
        }

        return ans;
    }
};