C语言实现优先队列、二叉堆和堆排序

排序与查找算法目录

【归并排序。桶排序】C语言实现归并排序、计数排序、桶排序、基数排序

【C语言实现交换排序】交换排序（冒泡排序、快速排序）

【C语言实现插入排序】插入排序（直接、折半、二路、希尔）

【三大经典查找】三大经典查找（跳跃、插值、斐波那契）

【三大基础查找】三大基础查找（顺序、二分、分块）

---

目录

一、优先队列和二叉堆

1.二叉堆的概念

2.堆的性质

3.优先队列

二、优先队列的实现

1.插入

 2.删除最小值

三、堆排序

---

 前言

查找和排序是数据结构与算法中不可或缺的一环，是前辈们在算法道路上留下的重要且方便的一些技巧，学习这些经典的查找和排序也能让我们更好和更快的解决问题。在这个专栏中我们会学习六大查找和十大排序的算法与思想，而本篇将详细讲解其中的堆排序；

注意：本文中所有排序按照升序排序，降序只需要把逻辑反过来即可！

---

一、优先队列和二叉堆

1.二叉堆的概念

在学习堆排序之前，我们先要学习二叉堆（binary heap）；

如果说数据结构中的栈是模仿硬件中的栈而构建的，那么堆完全不是一回事！二叉堆是一个基于完全二叉树的数据结构（在下文中简称堆）；

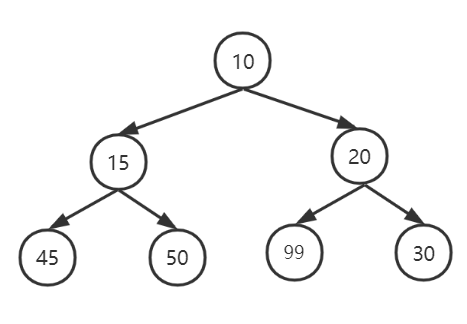
如同二叉查找树一样，堆也有两个性质：

• 结构性和堆序性；

正如AVL树一样，对堆的操作很可能破坏这两个性质中的一个，所以堆的操作必须要到堆的性质都被满足才能停止；

一项重要的观察发现，因为完全二叉树的规律性，所以它可以用一个数组而不需要指针来表示；

•  我们可以通过数学关系得到：在从下标为0开始的数组中，如果一个父节点的下标为x，那么它的左孩子的下标是2 * x + 1，它的右孩子的下标是2 * x + 2，同样的可以反推父节点的下标是(x - 1) / 2；

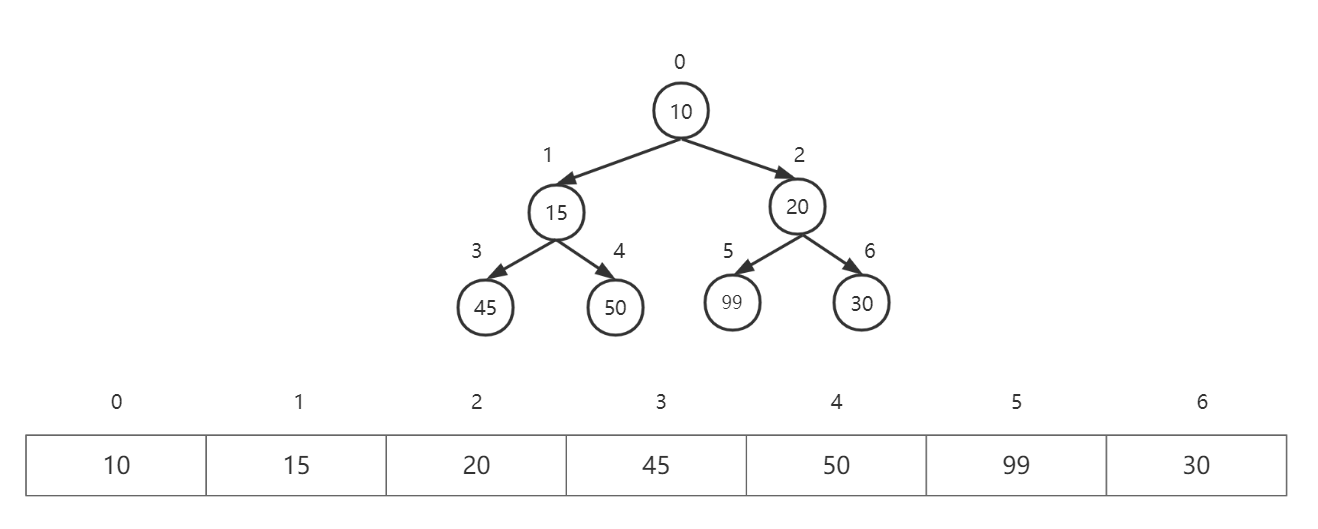
 也就是说，一个堆数据结构将由一个数组、一个代表最大值的整数和当前堆的大小组成； 

2.堆的性质

堆分为大顶堆和小顶堆： 

• 大顶堆 根节点的值永远大于孩子；

• 小顶堆 根节点的值永远小于孩子；

这正是堆序性（heap order）的体现，根据这个性质我们能够快速地找出最小值或最大值，因为最小值或最大值永远在根上；

3.优先队列

在实际项目中通常会有多项工作，而其中有一项特别重要的工作要先去做，那么这个工作就应该拥有优先权；针对这种特殊应用场景的队列，我们称之为：优先队列（PriorityQueue）；

不难看出，优先队列要求队列中的每一个元素都具有一定的优先级；优先级高的或优先级低的（人为定义的）要先出队，而优先级相同就按照顺序依次出队，先进先出；

二叉堆就刚好能够满足优先队列的需求；

二、优先队列的实现

根据上文中讲述的堆的性质，我们能很容易构建出二叉堆和优先队列：

typedef int ElementType;
typedef struct HeapStruct
{
	int capacity;//容量
	int size;//当前的大小
	ElementType* elements;//元素指针
}Heap, *PriorityQueue;