数组详解与实践-优快云博客

本文链接：https://blog.youkuaiyun.com/Yzy_fulture/article/details/121350511

1. 数组简介

1.1 数组定义

数组（Array）：一种线性表数据结构。它使用一组连续的内存空间，来存储一种具有相同类型的数据

数组就是相同类型的数据元素构成的有序集合。

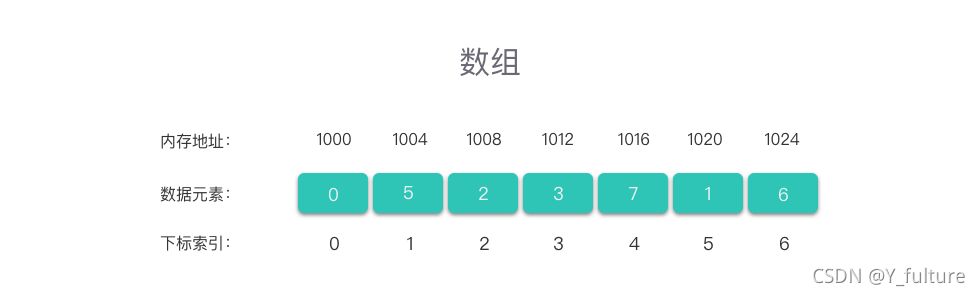
在这里插入图片描述
从上图可以得到的值得注意的点：

内存地址连续
下标索引从0开始，到n-1结束（n为数组中元素的数量）

因此，从另一方面来说，数组可以看作是使用了顺序存储结构的线性表的一种实现方式。

1.2 数组的随机访问

数组可以根据下标，直接定位到某一个元素存放的位置

在数组创建之初，计算机会给数组一个首地址作为数组开始的位置，之后通过寻址公式来定位某个元素对应的内存地址，然后访问该地址上的数据元素

寻址公式：下标i对应的数据元素地址 = 数组首地址 + i * 单个元素所占内存大小

1.3 多维数组

二维数组是一个由m行n列数据元素构成的特殊结构，本质上是以数组作为数据元素的数组，即数组的数组。
第一个维度为行，第二个维度为列

一般与矩阵结合使用

1.4 不同语言的数组的实现

C / C++:使用一块存储相同类型数据的、连续的内存空间。不管是基本类型数据，还是结构体、对象，在数组中都是连续存储的
Java：是存储相同类型数据的，但所使用的内存空间却不一定是连续（多维数组中）。且如果是多维数组，其嵌套数组的长度也可以不同。
Python：没有数组的概念，而是使用了类似Java中ArrayList容器类数据结构，叫做列表。Python 中列表存储的数据类型可以不一致，数组长度也可以不一致

2. 数组的基本操作

2.1 查:ls[i]

通过数组的寻址公式直接找到数据元素所在的位置
时间复杂度为O(1)

2.2 改:ls[i] = val

检查位置是否合法，若合法，直接将val复制到ls[i]
时间复杂度为O(1)

2.3 增

在数组末尾添加数据：ls.append(val)
1. 数组容量满时会开辟新的空间进行插入
2. 时间复杂度为O(1)
在数组中间添加数据：ls.insert(i, val)
1. 确定位置后，该位置后的元素依次向后移动一个单位
2. 时间复杂度为O(n)![](https://img-blog.csdnimg.cn/38ff6fb3e8d04915a1205c4e78428750.png?x-oss-process=image/watermark,type_ZHJvaWRzYW5zZmFsbGJhY2s,shadow_50,text_Q1NETiBAWV9mdWx0dXJl,size_20,color_FFFFFF,t_70,g_se,x_16

2.4 删

在数组末尾删除数据：ls.pop()
1. 将元素计数值减一即可
2. 时间复杂度为O(1)
在数组中间删除数据：ls.pop(i)
1. 确定位置后，该位置之后的元素依次向前移动一个单位
2. 时间复杂度为O(n)
基于条件删除数据：ls.remove(val)
1. 循环检查元素，查找的元素后将其删除，最后移动元素
2. 时间复杂度为O(n)

3. 数组的基础题目

66.加一

1. 将数组转换为整数在转换为数组

class Solution:
    def plusOne(self, digits: List[int]) -> List[int]:
        n = len(digits)
        for i in range(n):
            digits[i] = str(digits[i])
        num = int(''.join(digits))
        num = num + 1
        res = list(str(num))
        for i in range(len(res)):
            res[i] = int(res[i])
        return res

时间复杂度：O(n)
空间复杂度：O(n)

2. 找出最长的后缀

整体思路：
找到数组的后缀有多少个9

没有9，直接对最后一个元素进行加一操作
有若干个9，对从后往前数第一个不是9的元素进行加一操作，将后面的9都转换为0
全是9，将第一个元素变为1，其余元素全变为0，再在最后添加一个元素0

class Solution:
    def plusOne(self, digits: List[int]) -> List[int]:
        n = len(digits)
        for i in range(n-1, -1, -1):
            if digits[i] != 9:
                digits[i] = digits[i] + 1
                for j in range(i+1, n):
                    digits[j] = 0
                return digits
        # 全是9的情况
        digits.append(0)
        digits[0] = 1
        for i in range(1, n):
            digits[i] = 0
        return digits

时间复杂度：O(n)
空间复杂度：O(1)

724:寻找数组的中心下标.

1. 计算前缀和与后缀和

计算每个下标对应的左边的和以及右边的和，判断是否相等即可

class Solution:
    def pivotIndex(self, nums: List[int]) -> int:
        n = len(nums)
        if n == 1 or n == 2:
            return -1
        count_left = 0
        count_right = sum(nums) - nums[0]
        if count_left == count_right:
            return 0
        for i in range(1, n):
            count_left += nums[i - 1]
            count_right -= nums[i]
            if count_left == count_right:
                return i
        return -1

时间复杂度：O(n)
空间复杂度：O(1)

189.旋转数组

1. 使用额外的数组来存储中间数据

通过中间变量来存储截取的数组

class Solution(object):
    def rotate(self, nums, k):
        n = len(nums)
        k = k % n
        temp = nums[n-k:]
        nums[k:] = nums[:n-k]
        nums[:k] = temp

2. 翻转数组

按照题意，将原数组向右移动k次后，尾部的k%n个元素会移动到头部，其余元素向后移动k%d步
通过两次翻转将尾部的k%d个元素翻转到头部，再分别翻转[0, k%n - 1]和[k%n-1, n-1]即可得到结果
在这里插入图片描述

class Solution(object):
    def rotate(self, nums, k):
        n = len(nums)
        k = k % n
        nums.reverse()
        nums[:k] = list(reversed(nums[:k]))
        nums[k:] = list(reversed(nums[k:]))

时间复杂度：O(n)
空间复杂度：O(1)

3. 环形转换

注意，在这种情况下可能出现闭环现象，从而导致需要重新选择起始点来完成整体的移动

class Solution:
    def rotate(self, nums, k):
        k = k % len(nums)
        cnt = 0
        start = 0
        while cnt < len(nums):
            current = start
            pre = nums[start]
            while True:
                nxt = (current + k) % len(nums)
                nums[nxt], pre = pre, nums[nxt]
                current = nxt
                cnt += 1
                if start == current:
                    break
            start += 1

时间复杂度：O(n)
空间复杂度：O(1)

48. 旋转图像

1. 使用辅助数组

通过使用辅助数组来存储旋转过后的数据

class Solution:
    def rotate(self, matrix: List[List[int]]) -> None:
        n = len(matrix)
        ls = [[] for i in range(n)]
        for i in range(n):
            for j in range(n-1, -1, -1):
                ls[i].append(matrix[j][i])
        matrix[:] = ls

时间复杂度：O(n**2)
空间复杂度：O(n**2)

2. 翻转数组

通过观察，将数组先进行水平轴翻转，在进行主对角线翻转即可得到最终结果

class Solution:
    def rotate(self, matrix: List[List[int]]) -> None:
        n = len(matrix)
        # 水平翻转
        for i in range(n // 2):
            for j in range(n):
                matrix[i][j], matrix[n - i - 1][j] = matrix[n - i - 1][j], matrix[i][j]
        # 主对角线翻转
        for i in range(n):
            for j in range(i):
                matrix[i][j], matrix[j][i] = matrix[j][i], matrix[i][j]

时间复杂度：O(n**2)
空间复杂度：O(1)

3. 环形转换

通过一次性对四个数据进行位置的交换（通过数学的推导得出），同时采用一个中间变量来存储被覆盖的数据，可以实现直接在原数组位置上的修改。

class Solution:
    def rotate(self, matrix: List[List[int]]) -> None:
        n = len(matrix)
        for i in range(n // 2):
            for j in range((n + 1) // 2):
                matrix[i][j], matrix[n - j - 1][i], matrix[n - i - 1][n - j - 1], matrix[j][n - i - 1] \
                    = matrix[n - j - 1][i], matrix[n - i - 1][n - j - 1], matrix[j][n - i - 1], matrix[i][j]