哈夫曼树~

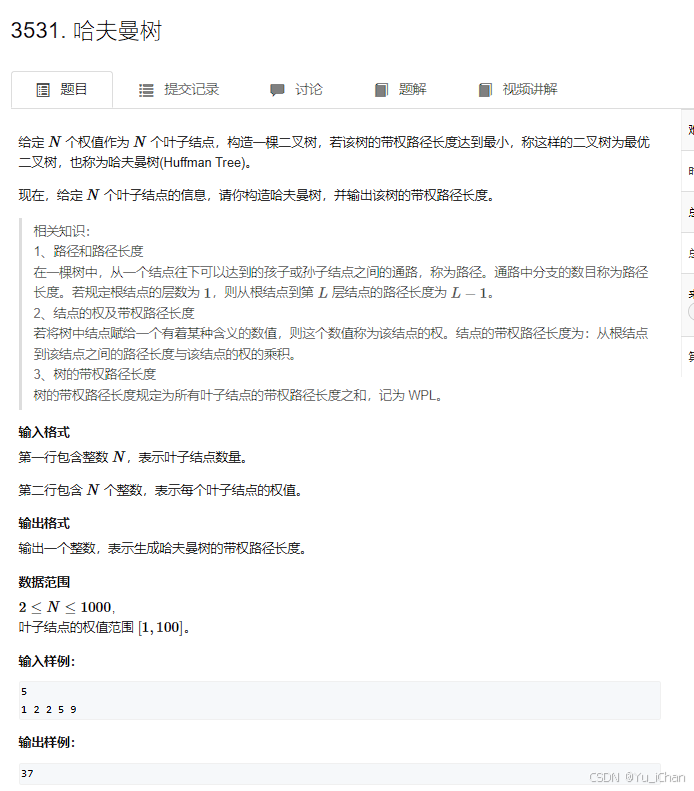
本题给我们n个节点要我们求其构成的哈夫曼树的带权路径长度，这个一般有两种求法，书面上的。求每个叶子节点的路径长度✖权值并且相加，或者将每一个非叶子节点的权值相加即为答案。

代码实现第二种的更为方便，因为第一种需要求路径长度。

由于哈夫曼树是每次合并最小的两个节点，所以我们需要用到一个数据结构——堆。每次将取出堆顶的两个元素，并且合并，合并后可以将它理解为一个新节点，直至堆中只有最后一个节点。

每次合并出的一个节点必是非叶子节点所以我们定义一个ans每次加上即可。

#include<iostream>
#include<vector>
#include<queue>
using namespace std;

int n;

int main()
{
    cin>>n;
    priority_queue<int,vector<int>,greater<int>>heap;
    for(int i=0;i<n;i++)
    {
        int x;
        cin>>x;
        heap.push(x);
    }
    int ans=0;
    while(heap.size()>1)
    {
        int a=heap.top();heap.pop();
        int b=heap.top();heap.pop();
        ans+=a+b;
        heap.push(a+b);
    }
    cout<<ans<<endl;
    return 0;
}

重点在于记住小根堆的定义方法，大根堆的话是默认是大根堆定义，即priority_queue<int>这种