12. 矩阵中的路径

剑指offer 12 矩阵中的路径 LeetCode79

79. 单词搜索

请设计一个函数，用来判断在一个矩阵中是否存在一条包含某字符串所有字符的路径。路径可以从矩阵中的任意一格开始，每一步可以在矩阵中向左、右、上、下移动一格。如果一条路径经过了矩阵的某一格，那么该路径不能再次进入该格子。例如，在下面的3×4的矩阵中包含一条字符串“bfce”的路径（路径中的字母用加粗标出）。

[[“a”,“b”,“c”,“e”],
[“s”,“f”,“c”,“s”],
[“a”,“d”,“e”,“e”]]

但矩阵中不包含字符串“abfb”的路径，因为字符串的第一个字符b占据了矩阵中的第一行第二个格子之后，路径不能再次进入这个格子。

示例 1：

输入： board = [[“A”,“B”,“C”,“E”],[“S”,“F”,“C”,“S”],[“A”,“D”,“E”,“E”]], word = “ABCCED”
输出： true

示例 2：

输入： board = [[“a”,“b”],[“c”,“d”]], word = “abcd”
输出： false

提示：

1 <= board.length <= 200
1 <= board[i].length <= 200
注意：本题与主站 79 题相同：https://leetcode-cn.com/problems/word-search/

解题思路：

注意，这是经典的介绍回溯法思想的题目，大部分回溯和dfs的题都会用到这里的代码模式，应牢牢掌握。如：

1. 上下左右四个方向的调整技巧（偏移量技巧）
2. 标记数组的设置
3. 回溯时的状态清除（恢复现场）

上述三个技巧应深入理解，之后做类似题才能游刃有余。

使用回溯法（backtracking）进行求解

回溯法是一种暴力搜索方法，通过搜索所有可能的结果来求解问题。

1. 由于路径不能重复进入矩阵的格子，所以需要定义和字符矩阵大小一样的布尔值矩阵，用来标记路径是否已经进入过该格子。
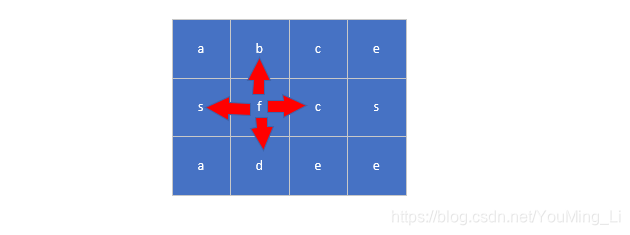
2. 回溯法在一次搜索结束时需要进行回溯（回退），将这一次搜索过程中设置的状态进行清除，从而开始一次新的搜索过程。例如下图示例中，从 f 开始，下一步有 4 种搜索可能，如果先搜索 b，需要将 b 标记为已经使用，防止重复使用。在这一次搜索结束之后，需要将 b 的已经使用状态清除，并搜索 c。
   

Java代码

class Solution {
    public boolean exist(char[][] board, String word) {
        if(board == null || board.length == 0) return false;
        int rows = board.length;
        int cols = board[0].length;
        boolean[][] isVisited = new boolean[rows][cols];//标记数组
        //路径可以从矩阵中任意一格开始，所以分别以矩阵中的每一个字符作为起点寻找
        for(int i = 0; i < rows;i++){
            for(int j = 0; j < cols; j++){
                if(dfs(board,word,0,i,j,isVisited)){
                    return true;
                }
            }
        }
         return false;
    }

    //参数说明，n表示当前访问到第几个字符了，（x,y）表示当前要访问的字符在board中的坐标
    private boolean dfs(char[][] board,String word,int n,int x,int y,boolean[][] isVisited){
        //当前位置和我们需要的字符word.charAt(n)不同，该路径行不通
        if(board[x][y] != word.charAt(n)) return false;
        //我们要查找的最后一个字符都通过了上面那条if语句，该单词路径存在
        if(n == word.length() - 1) return true;
        
        isVisited[x][y] = true;//标记board[x][y]已经被访问过了
        
        //定义左右上下四个方向(偏移量技巧）
        int[] dx = {-1,1,0,0};
        int[] dy = {0,0,-1,1};
        for(int i = 0; i < 4;i++){//分别尝试往左右上下四个方向走
            //改变方向，注意这里不是用x = x+dx[i],而是用a和b接收，以保证下轮for循环时x,y是原来的值
            int a = x + dx[i];
            int b = y + dy[i];
            //保证a,b不越界，且board[a][b]还未被访问过
            if(a >= 0 && a < board.length && b >= 0 && b < board[0].length && !isVisited[a][b]){
                 if(dfs(board,word,n+1,a,b,isVisited)){
                     return true;
                }
            }
        }
        isVisited[x][y] = false; //状态回退
        return false;
    }
}

go代码

func exist(board [][]byte, word string) bool {
    if board == nil || len(board) == 0 || len(board[0]) == 0 { return false }
    row , col := len(board) , len(board[0])
    // 注意go中二维切片的初始化方法，和JavaList<List<Boolean>>类似，泛型里面还需要需用new初始化
    // 而go中的二维切片其实是先用make初始化元素个数，一个元素就是一个[]bool切片，里面每个元素也需要用make初始化
    isVisited := make([][]bool,row)
    for i:= 0; i < row;i++ {
        isVisited[i] = make([]bool,col)
    }

    // 每个字符都可能成为起点
    for i := 0;i < row;i++ {
        for j := 0; j < col;j++{
            if dfs(board,word,0,i,j,isVisited) {
                return true
            }
        }
    }
    return false
}

func dfs(board [][]byte,word string,n,x,y int,isVisited [][]bool) bool {
    if board[x][y] != word[n] { return false }
    if n == len(word) - 1 { return true }

    isVisited[x][y] = true
    dx := []int{-1,1,0,0}
    dy := []int{0,0,-1,1}
    for i := 0 ; i < 4;i++ {
        a , b := x + dx[i],y + dy[i]
        // 确保索引不越界并且board[a][b]还没有被访问过
        if a >= 0 && a < len(board) && b >= 0 && b < len(board[0]) && !isVisited[a][b] {
            if dfs(board,word,n + 1,a,b,isVisited) {
            return true
           }
        }
        
    }
    isVisited[x][y] = false//状态回退
    return false
}

对状态回退的深入理解

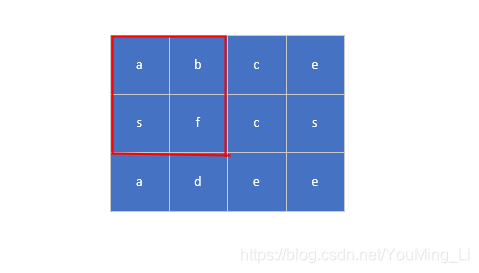
假设要找的路径是basf，访问b后，假如往下走访问了f,此时会标记f为访问状态了，但显然f不是路径的第二个字符a,故该路径不通，需要回溯到b，换个方向走，此时就应该将f的访问状态回退到未访问状态了，因为之后b换方向走后经过辗转还是可以访问到f来的，比如，回溯后现在换成往左走，则访问a，后续以此类推，慢慢的又会访问到f的，而经过回退后的f此时确实是未访问状态的，可以访问，因此basf路径找到了。