合唱队形（详解）

合唱队形是C++的经典题目，在东方博宜OJ有。

题目：

我们能找到规律。先把上图7个数从大到小排序：

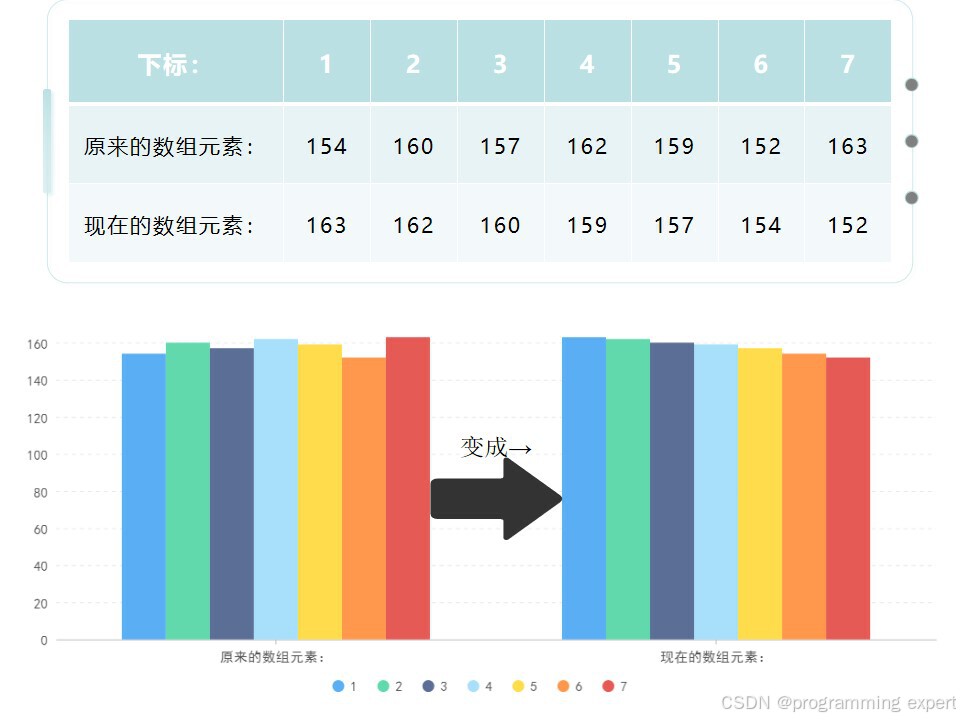
 接着，我们可以定义一个copy数组，来从中间开始（模拟）：

 题解：

方法一：

我们经过绞尽脑汁地思考，能发现：

输出的结果，下标分别是：1、3、5、7、6、4、2。下标1~n/2+1都是升序的单数（奇数），下标n/2+2~n都是降序的双数（偶数）。（这种方法是从小到大！）

#include<bits/stdc++.h>
using namespace std;
int n,a[55];//定义 
int main(){
	cin>>n;
	for(int i=1;i<=n;i++)
		cin>>a[i];
	sort(a+1,a+1+n);//排序 
	for(int i=1;i<=n;i+=2)
		cout<<a[i]<<" ";  //输出奇数 
	for(int i=n-1;i>0;i-=2)
		cout<<a[i]<<" ";//再输出偶数 
	return 0;
}

输出结果：

方法二：

存数组。

#include <bits/stdc++.h>
using namespace std;
/*
思路：通过观察规律，如果有7个数；)是10 20 30 40 50 60 70
排队的结果：
10 30 50 70 60 40 20
第1个数~n/2+1个数，分别是原来数组按从小到大排序的：第1 3 5 7...个数
倒数第10数~倒数n/2个数值，分别是原来数组的第的2 4 6...个数
*/
int a[60],n,b[60];//b数组存储结果
int main(){
    cin>>n;
    for(int i=1;i<=n;i++)
		cin>>a[i];
    sort(a+1,a+n+1);
    for(int i=1;i<=n/2+1;i++)
		b[i]=a[i*2-1];
    int k=1;//k用来标记a数组下标
    //赋值后一半
    for(int i=n;i>n/2+1;i--)
    {
        b[i]=a[k*2];
		k++;
        
    }
	for(int i=1;i<=n;i++)
	    cout<<b[i]<<" ";
    return 0;
}

方法三：

用容器。

#include<bits/stdc++.h>
using namespace std;
int print(const deque<int>&dq){
	for(int i=0;i<dq.size();i++)
		cout<<dq[i]<<" ";
}
int n,a[505];
deque<int>dq;
int main(){
	cin>>n;
	for(int i=1;i<=n;i++)
		cin>>a[i];
	sort(a+1,a+1+n,greater<int>());
	for(int i=1;i<=n;i++)
	{
		if(i%2==1) dq.push_front(a[i]);
		if(i%2==0) dq.push_back(a[i]);
	}
	print(dq);
	return 0;
}