1146 Topological Order (25 分) 拓扑排序 判定

也不写题干了，主要说说拓扑排序。

对一个有向图G，我们把满足下列要求的顶点序列叫做G的拓扑排序，一般来说，一个图的拓扑排序不唯一。

（1）拓扑排序中的，对每一个节点，它的后继节点都在该节点之后出现。
（2）如果两节点没有直接间接的前驱后继关系，则两节点在序列中先后顺序不限
（3）每个拓扑排序包含G的所有节点

有向无环图（简称DAG）：没有回路的有向图叫做有向无环图。

比如下图（就是pat 甲级1146样例中的图）

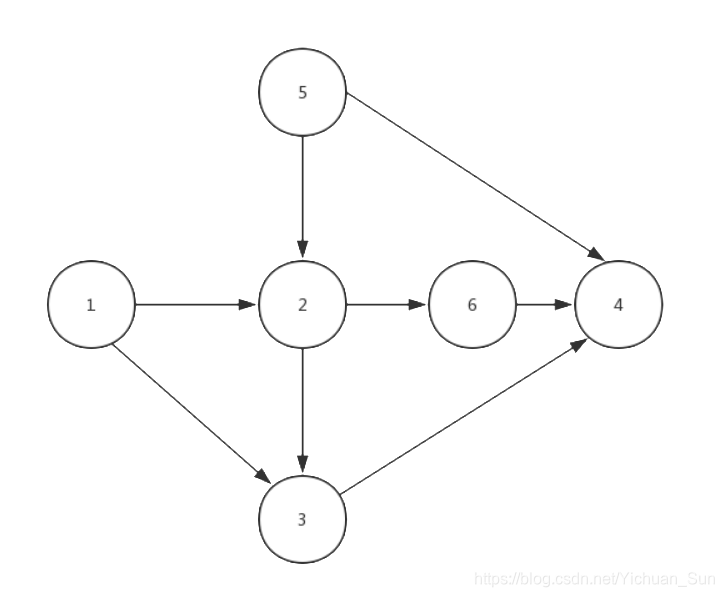
样例给出了如下数据

1 5 2 3 6 4
5 1 2 6 3 4
5 1 2 3 6 4
5 2 1 6 3 4
1 2 3 4 5 6

由图可知，（序列号从0开始）序列3,4违反了规则，2在1之前（序列3），4在5之前（序列4）。

回到我们的对拓扑排序的解释，如何确定一个图的拓扑排序呢？可以采用这种算法：
（1）将图的入度为0的节点入队
（2）队首节点v出队，输出该节点v的值，它的后继节点w的入度均-1，并且每次-1时均判断w的入度是否为0，如果为0，同样入队。
（3）重复2步骤，直到图为空或者不再存在无前驱的节点。如果是后者，则图中存在环。

当然，队列也可以用栈替代。

回到这个题的解法，那就很简单了。由于拓扑排序算法运行时，每次输出的节点的入度都为0，所以，在用题目中给出的序列模拟算法执行过程时，每次输出的节点的出度必为0，否则就不是一个拓扑排序。

• 如果有数组data* a，则vector<data> v(a,a+sizeof(a))就可以将整个数组复制到向量中，这是vector的一种构造方法，两个参数相当于指针

代码如下。

#include <bits/stdc++.h>
#define N 1005
using namespace std;
vector<int> vi[N],ans;		//vi是图的邻接表表示 
int din[N];
int main(){
    int n,m,k;
    scanf("%d%d",&n,&m);
    for (int i=0;i<m;i++)   {
        int a,b;
        scanf("%d%d",&a,&b);
        vi[a].push_back(b);
        din[b]++;
    } 
    scanf("%d",&k);
    for (int p=0;p<k;p++) {
        int flag=0;
        vector<int> tv(din,din+n+1);
        for (int i=0;i<n;i++)   {
            int t;
            scanf("%d",&t);
            if (tv[t]!=0)  flag=1;		//,入度非0，说明该序列不是拓扑排序 
            for (int j=0;j<(int)vi[t].size();j++)
                tv[vi[t][j]]--;		//vi[t][j]意为节点t的第j个后继节点 
        }
        if (flag)   ans.push_back(p);
    }
    printf("%d",ans[0]);
    for (int i=1;i<(int)ans.size();i++) printf(" %d",ans[i]);
    printf("\n");
    return 0;
}

复杂度：这我还真不会算了，但是应该小于等于O(k*n²)。