【论文精读】最有潜力的Transformer杀手-谷歌发布新LLM模型架构：MOR

• 标题：Mixture-of-Recursions: Learning Dynamic Recursive Depths for Adaptive Token-Level Computation（递归混合模型：为自适应令牌级计算学习动态递归深度）
• 论文链接：https://arxiv.org/abs/2507.10524
• 作者：Sangmin Bae¹、，Yujin Kim¹、，Reza Bayat²、*，Sungnyun Kim¹，Jiyoun Ha³，Tal Schuster⁴，Adam Fisch⁴，Hrayr Harutyunyan⁵，Ziwei Ji⁴，Aaron Courville²、⁶、†，Se-Young Yun¹、†
  ¹KAIST人工智能研究所，²米拉研究所，³谷歌云，⁴谷歌DeepMind，⁵谷歌研究院，⁶蒙特利尔大学
  *同等贡献，†通讯作者
• 代码链接：https://github.com/raymin0223/mixture_of_recursions.git

背景🚉

1. 为什么需要MOR？
   想象一下，在我们使用大模型（GPT/DeepSeek）时，输入的每句话都会被背后的大模型“思考”后回复。但是现在几乎所有的模型的都存在一个问题：不管发送的内容是简单还是复杂，都需要使用相同的计算资源。比如你发送一个“嗯”或者给它一道复杂的数学难题，模型都会“全力以赴”，导致计算成本高，速度慢。

   同时，大模型参数持续增长（从几十亿到几千亿），无论是训练还是运行时，内存、电力都随着参数而暴涨。研究者就在思考一个问题：能否让模型自己本身动态且灵活的分配资源？在模型参数更少的同时，能力不打折？

   MOR就是为了解决这两个问题诞生——既减少参数（省钱省内存），同时按需分配计算里（高效）

2. 发展历程：从”笨办法“到MOR的突破

   • 早期模型：“一视同仁”的计算
     最早的Transformer模型（比如GPT、BERT）就像“强迫症”，每句话里面的每个词（token)，都需要经过固定层数的计算，比如“的”和“量子力学”，都是享受一样的”待遇“，造成算力浪费。

   • 参数共享（parameter sharing）：减少模型大小
     后来研究者发现，模型的很多层其实可以“重用”——比如把三层网络堆叠起来，也就是重复用三次模型，假装层九层，增加网络深度，这样参数量减少到1/3，但能力差不多，这就是"递归Transformer，Recursive Transformer””。
     但问题在于：参数减少了，但是计算量没有减少，每个token 仍然需要走完全部流程！

   • 自适应算法adaptive computation）：让模型“偷懒”
     再后来，有人提出Early exiting（早期退出）：模型处理到一般，如果觉得”这个词我已经懂了"，就提前停止计算，（比如简单的Token经过两层就停，复杂的token8层）。但这种方法的缺点是:需要额外训练一个“裁判”模型，来决定什么时候退出。麻烦还荣誉出错

   • MOR 的诞生：把两者结合起来
     MOR就像“集大成者”

   • 继承了”参数共享”的优点：用一套参数重复多次（递归， recursion），参数少但能力强。

   • 又加入了 智能路由（routing): 每个token经过一个轻量的“路由器（router) ,决定它需要递归几次，（比如简单的词递归1次，复杂的词递归3词）。

   • 优化内存：只缓存需要计算词的中间结果（键值对，key-value-pairs），进一步提速（因为每个token有自己对应的递归深度，通过递归深度处理完毕后，信息就没有必要保存且向下流动了）。

3. MOR的核心思路：简单说就是3点

   1. 参数共享不浪费：一套参数反复用，比如用3层参数递归3次，相当于9层的效果，但参数只有1/3。
   2. 令牌“按需递归”：每个词（token）通过“路由器（router）”判断难度，难的词多递归几次（多计算），简单的词少递归（少计算）。
   3. 缓存“精打细算”：只保留还需要计算的词的中间结果（KV缓存，key-value caching），减少内存占用，让模型跑得更快。

4. 为什么MOR重要？

   • 对用户：聊天、写东西时，AI回复更快，手机/电脑不卡顿。
   • 对企业：训练和运行成本降低（参数少+算力省），小公司也能用得起大模型。
   • 对技术：证明了“高效AI”的可能——不一定参数越多越好，而是“该省省，该花花”。

现在MOR已经在实验中打败了很多传统模型，未来可能会成为大模型的“标配”技术！

Abstract——摘要

翻译

缩放语言模型（scaling language models）解锁了令人印象深刻的能力，但其伴随的计算和内存需求使得训练和部署成本高昂。现有的效率优化工作通常要么针对参数共享（parameter sharing），要么针对自适应计算（adaptive computation），而如何同时实现这两者仍是一个未解决的问题。我们提出了递归混合模型（Mixture-of-Recursions，MoR），这是一个统一框架，在单个递归 Transformer（Recursive Transformer）中结合了这两个效率优化方向。MoR 通过在递归步骤中重用共享的层堆栈来实现参数效率（parameter efficiency），同时轻量级路由器（router）通过为单个令牌（token）动态分配不同的递归深度（recursion depth），实现自适应令牌级 “思考”。这使得 MoR 仅在特定递归深度下仍活跃的令牌之间进行二次（平方）注意力（attention）计算，通过选择性地仅缓存这些令牌的键值对（key-value pairs），进一步提高内存访问效率。除了这些核心机制，我们还提出了一种键值共享（KV sharing）变体，该变体重用第一次递归中的键值对，专门设计用于降低预填充（prefill）延迟和内存占用。在从 1.35 亿到 17 亿参数的模型规模上，MoR 形成了新的帕累托前沿（Pareto frontier）：在相同的训练 FLOPs 和更小的模型尺寸下，与普通 Transformer（vanilla Transformer）和现有递归基线（recursive baselines）相比，它显著降低了验证困惑度（validation perplexity），提高了少样本准确率（few-shot accuracy），同时实现了更高的吞吐量（throughput）。这些成果表明，MoR 是一条在不产生大模型成本的情况下实现大模型质量的有效路径。

讲解

• 背景：现在的大模型（如GPT、Llama）参数越来越多（从几十亿到几千亿），虽然能力变强了（能做推理、创作等），但训练时要花大量电费、用超多GPU，部署时普通设备跑不动（内存不够、速度太慢）。

• 问题：“规模扩张”和“成本可控”成了矛盾。

• 现有方案的局限：

  • 参数共享（parameter sharing）：让模型重复使用一组参数（比如用3层参数重复3次，假装成9层），减少参数总量（省钱省内存），但计算量没少（每个词还是要走完全程）。
  • 自适应计算（adaptive computation）：让简单的词少算几步（早期退出），复杂的词多算几步，减少计算量，但参数还是很多（没解决内存问题）。

• 核心痛点：这两种方法各管一段，没人把它们结合起来。

• MoR的定位：首次把“参数共享”和“自适应计算”捏到一起，用一个模型同时解决“参数多”和“计算浪费”两个问题。

• MoR的两大核心设计：

  • 参数共享：一套层（比如3层）重复用多次（比如3次），相当于9层的效果，但参数只有1/3（省内存）。
  • 动态路由：每个词（令牌）通过“路由器”判断自己要算几次（比如“的”算1次，“量子力学”算3次），避免浪费计算（省算力）。

• 衍生优势：

  • 注意力计算是模型中最耗时的部分（复杂度是“词数的平方”），MoR只让“仍在计算的词”参与，减少无效计算。
  • 只缓存这些活跃词的键值对（KV对），不存无用信息，进一步省内存、提速度。

• 额外优化：预填充（prefill）是处理输入文本的第一步，MoR通过复用第一次递归的KV对，让这一步更快、更省内存。

• 实验效果：

  • 帕累托前沿：同样的计算成本下，MoR的效果（准确率、困惑度）比其他模型更好；同样的效果下，MoR更省资源。
  • 具体表现：参数更少、训练计算量相同，但预测更准（困惑度低）、少样本任务更强，运行速度也更快（吞吐量高）。

🪧概念补充：

1. 缩放语言模型（scaling language models）：通过扩大参数、数据、计算量来提升模型能力的过程，是过去几年大语言模型能力爆发的核心驱动力。研究发现，语言模型的能力（如推理、少样本学习、生成质量等）与模型规模（参数数量）、训练数据量、计算量之间存在可预测的规律：当这些要素按比例增加时，模型的性能会稳步提升（这种规律被称为 “缩放定律，scaling laws”，Kaplan 等人 2020 年提出）。

2. “活跃的令牌”active tokens：指在当前递归步骤中仍需继续计算的令牌（未提前退出）。每轮递归结束后，路由器会根据令牌的 “复杂度”（通过隐藏状态计算的分数）判断是否让其继续参与下一轮递归：

   • 如果分数高于阈值，令牌保持 “活跃”，进入下一轮递归。
   • 如果分数低于阈值，令牌 “退出”，不再参与后续任何递归步骤（即变为 “非活跃”）。

3. 预填充（prefill）延迟：指在基于解码器的 Transformer 架构语言模型（如 GPT 类模型）推理时，从输入提示（问题）到生成第一个输出令牌（token）之间的时间延迟。它主要受输入提示长度、模型计算复杂度、硬件性能等因素影响。

4. “训练 FLOPs”？
   “FLOPs” 是Floating Point Operations的缩写，指 “浮点运算次数”—— 简单说，就是模型训练时进行的 “数学计算总量”。

1. Introduction

翻译

将 Transformer 网络扩展到数千亿参数，解锁了令人印象深刻的少样本泛化（few-shot generalization）和推理能力（reasoning abilities）。然而，随之而来的内存占用（memory footprint）和计算需求使得在超大规模数据中心之外进行训练和部署变得极具挑战性。这促使研究人员寻求替代的 “高效” 设计—— 减少或共享模型权重，以及自适应计算—— 仅在需要时投入更多计算，是两个极具前景且被积极研究的方向。

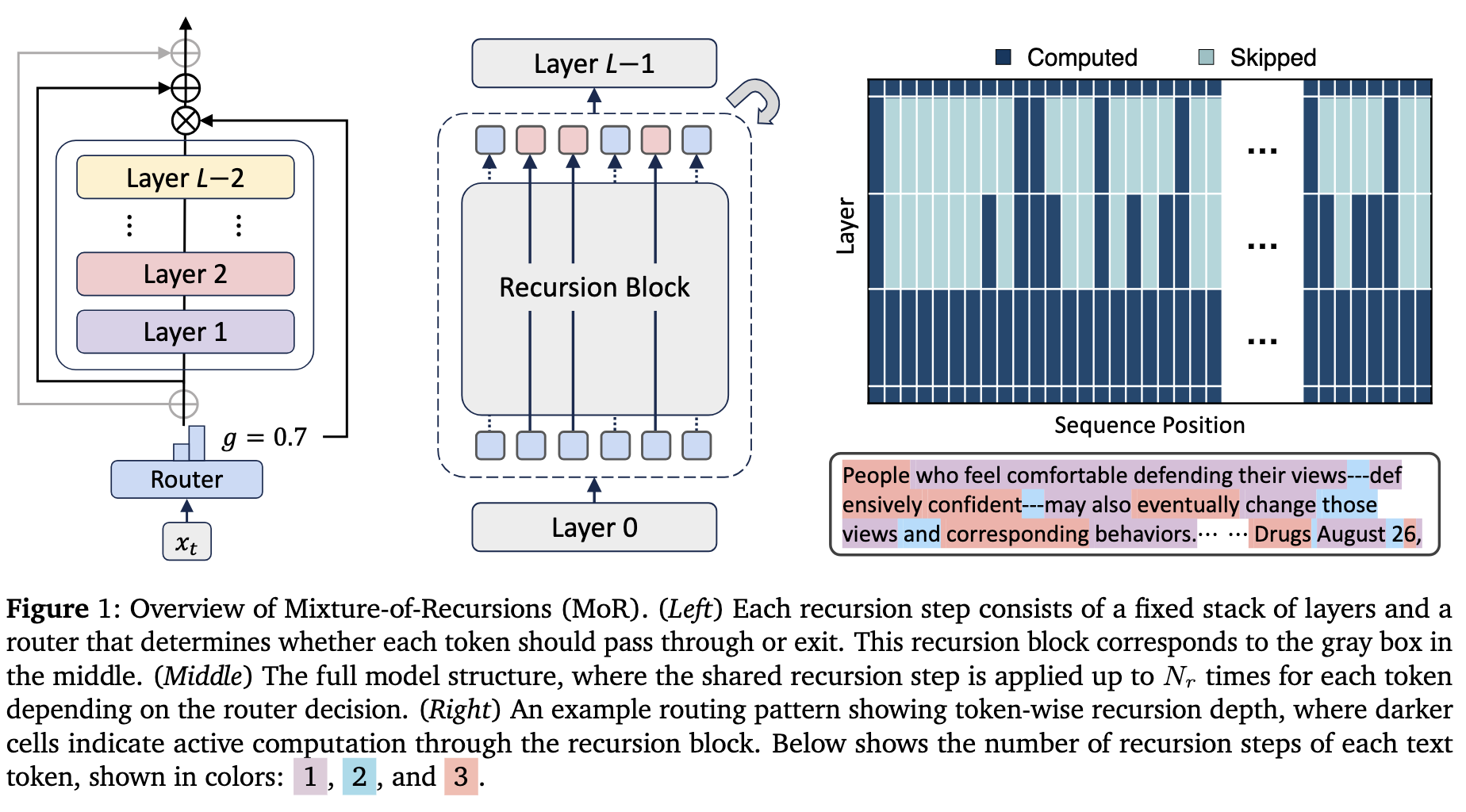
在这项工作中，我们提出了递归混合模型（MoR），这是一个充分利用递归 Transformer 潜力的统一框架（见图 1）。MoR 端到端（end-to-end）训练轻量级路由器，以分配令牌特定的递归深度：它根据每个令牌所需的 “思考” 深度，决定共享参数块（shared parameter block）应用于该令牌的次数，从而将计算导向最需要的地方。这种动态的令牌级递归本质上促进了递归级键值缓存（recursion-wise key-value caching），选择性地存储和检索与每个令牌分配的递归深度相对应的键值对。这种有针对性的缓存策略减少了内存流量（memory traffic），从而在不依赖事后修改的情况下提高了吞吐量。因此，MoR 同时实现了：
（i）通过绑定权重削减参数；
（ii）通过路由令牌削减冗余 FLOPs；
（iii）通过递归级键值缓存削减内存流量 —— 所有这些都在单个架构中实现。

从概念上讲，MoR 提供了一个潜在空间推理（latent space reasoning）的预训练框架 —— 通过迭代应用单个参数块进行非语言思考(non-verbal thinking)。然而，与在生成前对增强的连续提示（continuous prompts）进行思考的方法不同，MoR 直接在每个令牌的解码（decoding）过程中实现这种潜在思考此外，路由机制促进了沿模型垂直轴的自适应推理，超越了先前工作中常见的统一、固定思考深度本质上，MoR 使模型能够在每个令牌的基础上高效调整其思考深度，统一了参数效率和自适应计算。

Contribution：总之，我们在本文中的主要贡献如下：

1. 高效语言建模的统一框架：我们提出了递归混合模型（MoR），这是第一个在单个框架中统一效率范式 —— 参数共享（第 2.1 节）、令牌级自适应思考深度（第 2.2.1 节）和高效键值缓存（第 2.2.2 节）的架构。
2. 动态递归路由：我们引入了一种从头开始训练的路由器，用于分配动态的每令牌递归深度。这使训练与推理（inference）时的行为保持一致，并消除了传统早期退出方法中使用的昂贵、降低性能的事后路由阶段的需求。
3. 广泛的实证验证：在相同计算预算下，从 1.35 亿到 17 亿参数的模型中（见注释 2），MoR 通过相对于普通和递归基线提高验证损失（validation loss）和少样本准确率，建立了新的帕累托前沿Pareto frontier（第 3.1 节、第 3.2 节）。
4. 高效架构：MoR 通过仅让必要的序列参与注意力操作，显著减少了训练 FLOPs。同时，键值缓存大小的减少本身提高了推理吞吐量，而连续深度批处理（continuous depth-wise batching）进一步增强了这一效果（第 3.3 节）。

注 1：虽然这种思考沿深度轴进行，但类似于沿水平序列轴生成连续思考。
注 2：这些是基础模型大小，而 MoR 模型由于参数共享，具有更少的独特参数

讲解

🪧核心优势：

• ties weights to cut parameters（参数共享减少模型大小）：模型的 “参数” 就像做饭的 “调料”，MoR 不搞 “每种调料买一套”，而是 “一种调料反复用”，固定下来。比如用 3 种调料（参数）重复用 3 次，做出 9 种调料的效果，这样调料（参数）总数减少到 1/3，但味道（模型能力）差不多。
• routes tokens to cut redundant FLOPs（动态计算减少浪费）
  • FLOPs（浮点运算次数）是衡量计算量的单位，就像 “做饭的总步骤”。
  • 通俗理解：每个词（令牌）经过一个 “小裁判”（路由器），简单词（如 “的”）判定后少算几步（比如 2 步就停），复杂词（如 “量子”）多算几步（比如 5 步）。这样总步骤（FLOPs）减少，模型跑得更快。
• caches key-values recursion-wise to cut memory traffic（精准缓存省内存）
  • 内存 traffic 就是 “数据在内存里的流动量”，像 “快递运输量”。
  • 通俗理解：MoR 只缓存还需要继续计算的词的中间结果（比如还在 “活跃” 的令牌），像快递只送 “还没签收的包裹”，不浪费运力。这样内存里的数据流动减少，模型运行更流畅。

传统模型是 “大锅饭”：不管词简单复杂，都用全套参数、算满所有步骤、缓存所有数据。而 MoR 是 “自助餐”：

• 调料（参数）重复用（省钱）；
• 吃饭步骤（计算）按需来（省时间）；
• 餐盘（缓存）只给还在吃的人用（省空间）。

🪧核心创新

1. 核心概念：潜在空间推理（latent space reasoning）：

   • 通俗解释：AI 处理信息时，不一定需要把思考过程 “说出来”（生成文字），而是在 “脑子里”（潜在空间）默默完成推理。比如你解数学题时，心里算 “1+1=2”，不用出声，这就是 “非语言思考（non-verbal thinking）”。
   • MoR 的角色：MoR 通过 “递归参数块” 让模型反复琢磨（迭代），实现这种 “默默推理”，还不浪费资源。

2. 和传统方法的区别：

   • 传统方法（如 Liu et al., 2024b 等）：需要先写一段 “增强提示（augmented continuous prompts）”（比如给模型额外的解释文字），模型才会认真推理。就像你问问题时，得先写 “请一步一步分析”，模型才会多思考。
   • MoR 的不同：不用额外提示，模型自己判断每个令牌的难度，在 解码（decoding） 每个令牌时 “动态调整思考深度”。比如看到 “量子” 就多递归几次（多算），看到 “的” 就少算，全程 “自动操作”。

3. 垂直轴自适应推理：模型的 “智能分配”

   • 垂直轴（vertical axis）：可以理解为模型的 “计算深度”（比如递归次数 1→2→3 次），就像 “思考步骤” 的多少。
   • MoR 的突破：传统模型在垂直轴上 “一视同仁”（所有令牌都走满 3 次递归），而 MoR 让令牌 “按需停在不同深度”（有的停在 1 次，有的走到 3 次）。这种 “垂直轴上的动态调整”，就是 “自适应推理（adaptive reasoning）”。

2. Method

2.1 Preliminary预备知识

翻译

递归Transformer（Recursive Transformers.）：标准Transformer通过$L$个独特层的堆栈构建令牌表示，每个层都有一个自注意力和一个前馈网络。在时间步$t$，隐藏状态$h$的演变如下：${\mathbf{h}}_t^{\ell +1}=f({\mathbf{h}}_t^{\ell };{\Phi }_{\ell })$，其中$\ell =0,\dots ,L-1$，${\Phi }_{\ell }$表示第$\ell$层的参数。递归Transformer旨在通过跨深度重用层来减少参数数量。它们没有$L$组不同的权重，而是将模型划分为$N_r$个递归块，每个块使用共享的参数池${\Phi }^{\prime }$。这种设计允许在不增加参数大小的情况下进行更多计算（通过增加有效网络深度）。

参数共享策略Parameter-sharing strategies：我们研究了四种参数共享策略：循环（Cycle）、序列（Sequence）及其变体中间循环（Middle-Cycle）和中间序列（Middle-Sequence）。表1总结了两种主要设计，完整列表见附录中的表5。在循环共享中，递归块循环重用。例如，考虑一个具有$L=9$层的原始非递归模型及其使用$N_r=3$次递归的递归对应模型。在“循环”策略下，层的共享和展开方式为$[(0,1,2),(0,1,2),(0,1,2)]$。在“序列”共享中，每个递归块在进入下一层之前连续重用同一层，对于相同配置，结果为$[(0,0,0),(1,1,1),(2,2,2)]$。两者展开后的有效层数相同$(L=9)$，但顺序不同。此外，“中间”变体保留第一层和最后一层的全容量参数（${\Phi }_0$和${\Phi }_{L-1}$），而在中间层之间共享权重。

表1：递归Transformer中的参数共享策略。该表显示了具有循环层重用的循环和中间循环方案，其中中间循环保留独特的第一层和最后一层。

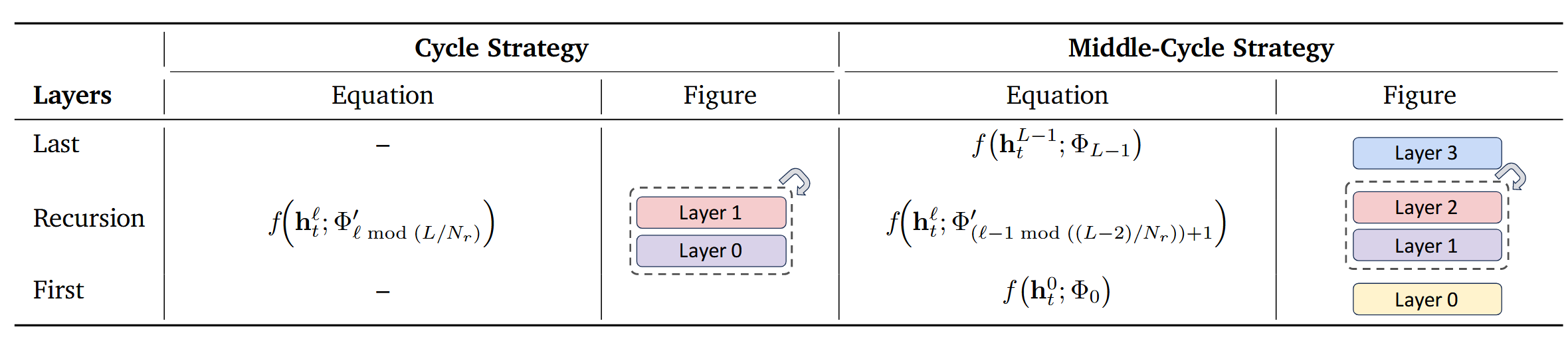
递归模型中增强的训练和推理效率：参数共享策略能将模型中独特的可训练参数数量减少到递归次数的N分之一，从而高效地降低模型的内存占用。从分布式训练的角度来看，当使用完全分片数据并行（FSDP） 时，这变得非常高效。以前，单次all-gather操作仅支持一次迭代（即1次迭代/收集），而递归模型在所有递归步骤中重用相同的收集参数（即$N_r$次迭代/收集）。此外，递归架构启用了一种新的推理范式——连续深度批处理。这种技术允许处于不同阶段的令牌被分组到单个批次中，因为它们都使用相同的参数块。这可以消除“气泡”——等待其他样本完成所花费的空闲时间——从而显著提高吞吐量。

讲解：

🪧分布式训练的效率革命（FSDP）

• FSDP（完全分片数据并行）：把模型参数拆分到多个 GPU，每个 GPU 只存一部分参数，训练时通过通信协作。
• MoR + FSDP 的化学反应：MoR 已经通过参数共享减少了 1/3 参数，再加上 FSDP 的分片，每个 GPU 的内存压力进一步降低（比如 12 层模型，参数经共享 + 分片后，单 GPU 只存 1/9）。
• 效果：以前 10 个 GPU 才能训的模型，现在 3 个 GPU 就够，还更快。

🪧递归模型的 “迭代效率”

• all-gather（全收集）：分布式训练中，每个 GPU 需要获取其他 GPU 的参数 / 中间结果，这个操作很耗时。

  每个 GPU（比如 4 个 GPU）把自己的局部参数 / 中间结果发给其他所有 GPU，同时接收别人的，最终每个 GPU 都拥有完整的全局信息（比如完整的模型参数、所有令牌的中间结果）

• 传统模型：1 次 all-gather 只能支撑 1 次迭代（iter）。

• MoR 的递归模型：1 次 all-gather 获取的参数，能重复用$N_r$次（比如获取 3 层参数，递归 3 次，支撑 3 次迭代），相当于 “1 次通信顶 3 次用”，通信成本降为 1/3。

---

先前工作的局限性：尽管模型参数是绑定的，但不同的键值缓存通常用于每个深度。这种设计无法减少缓存大小，这意味着高检索延迟仍然是一个严重的推理瓶颈。此外，大多数现有递归模型只是对所有令牌应用固定的递归深度，忽略了复杂性的差异。虽然像早期退出这样的事后方法可以引入一定的适应性，但它们通常需要单独的训练阶段，这可能会降低性能。理想情况下，递归深度应该在预训练期间动态学习，允许模型以数据驱动的方式使其计算路径适应每个令牌的难度。然而，这种动态路径引入了一个新的挑战：退出的令牌在后续递归深度中将缺少键值对。解决这一问题需要并行解码机制来高效计算实际的键值对，但这需要单独的复杂工程并使系统复杂化。

讲解：

🪧局限1：KV 缓存 “只增不减”，内存浪费严重

• 以前的递归模型虽然共享了参数（比如 3 层参数重复用 3 次），但每个递归深度（比如第 1 层、第 2 层、第 3 层）都要单独缓存所有令牌的 KV 对（中间结果）。
• 举例：10 个令牌经过 3 次递归，传统模型会缓存 10×3=30 组 KV 对，哪怕其中 5 个令牌在第 1 层就没用了，它们的 KV 对还是会被存到第 3 层。
• 后果：缓存越来越大，读取速度变慢（高延迟），成了推理时的 “卡脖子” 问题。

🪧局限2:计算 “大锅饭”，不管令牌难不难都算满

• 以前的递归模型对所有令牌 “一视同仁”，不管是简单词（如 “的”）还是复杂词（如 “相对论”），都强制走相同的递归次数（比如都算 3 次）。
• 问题：简单词白白浪费算力，复杂词可能还没算够，导致 “该省的没省，该花的没花”。

🪧局限3:“早期退出” 方法太麻烦，还影响效果

• 后来有人想了个办法 —— 让简单词提前退出（早期退出），但这个方法有问题：
  需要额外训练一个 “裁判模型” 来判断 “什么时候退出”，相当于多了一个步骤（单独训练阶段）；
  这个 “裁判” 可能判断不准，反而让模型效果下降（比如把复杂词误判为简单词，提前退出导致算错）。

🪧局限4：动态退出导致 KV 对缺失，工程上很难实现

• 就算让令牌动态退出（有的早走，有的晚走），新问题又出现了：
  • 提前退出的令牌，后续递归步骤里没有它们的 KV 对了，但注意力计算可能还需要用到这些信息（比如复杂词需要参考简单词的上下文）；
  • 要解决这个问题，得专门设计 “并行解码机制”（同时处理不同退出状态的令牌），但这需要复杂的工程优化，系统变得很繁琐，很难落地。

2.2. 递归混合模型

我们提出了递归混合模型（MoR）——一个在预训练和推理期间动态调整每个令牌的递归步骤的框架。MoR的核心在于两个组件：一个路由机制，用于分配令牌特定的递归步骤，以自适应地将计算集中在更具挑战性的令牌上；以及一个键值缓存策略，定义了键值对如何存储以及在每个递归步骤中如何选择性地用于注意力计算。

2.2.1. 路由策略：专家选择与令牌选择

翻译

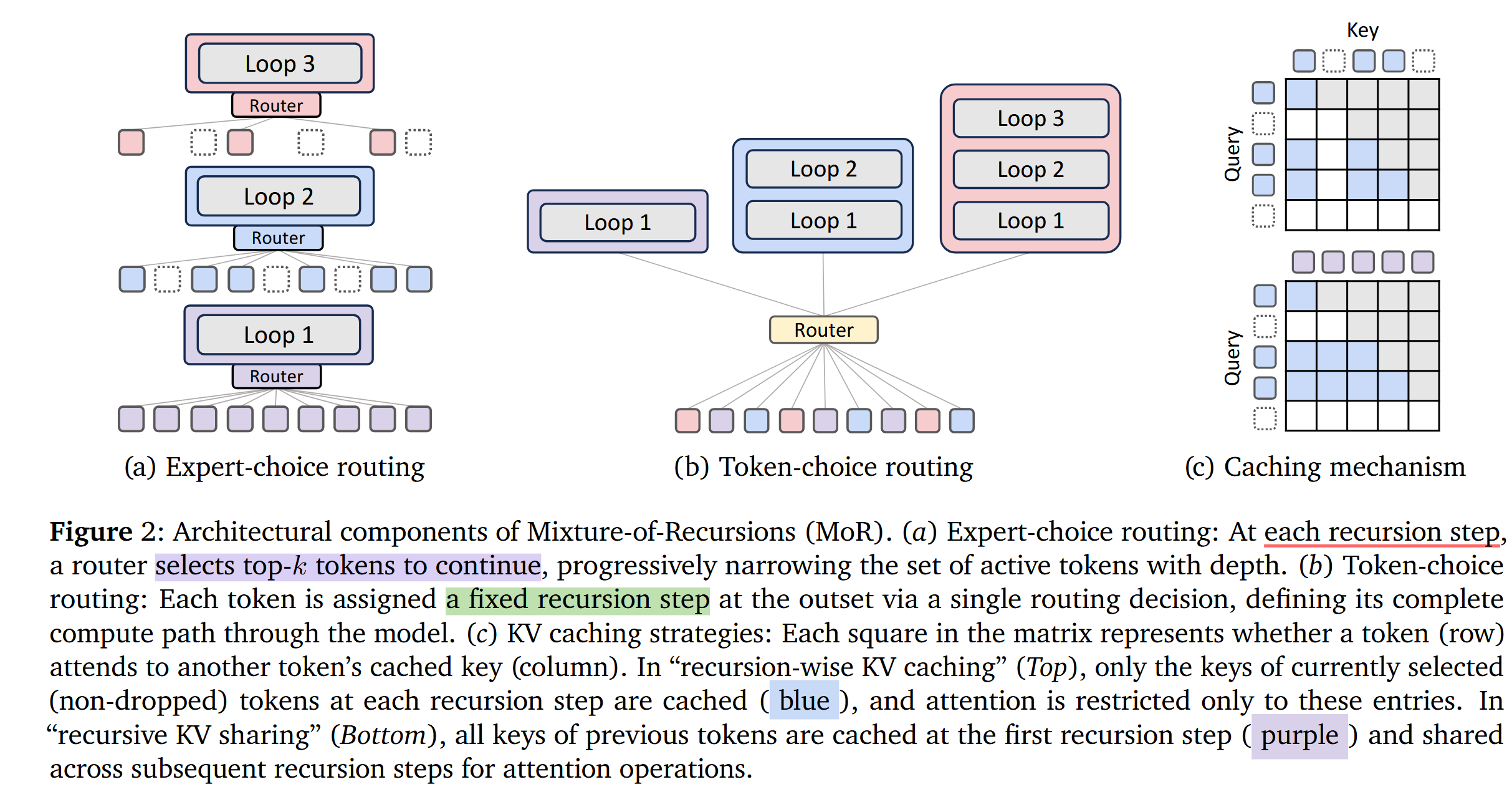
专家选择路由（图2a）：受MoD模型中的top-k门控启发，在专家选择路由中，每个递归深度成为一个专家，并选择它们偏好的top-k令牌（例如，对于$N_r=3$，我们有三个专家：专家1应用第一个递归步骤，专家2应用第二个递归步骤，依此类推）。在每个递归步骤$r$，相应的路由器使用隐藏状态$H_t^r$（第$r$个递归块的输入）及其路由参数${\theta }_r$计算令牌$t$的标量分数$g_t^r=G({\theta }_r^{\top }{H}_t^r)$。这里，$G$表示激活函数，如$sigmoid$或$tanh$。然后，选择top-k令牌通过递归块：

$${\mathcal{H}}_t^{r+1}=\{\begin{array}{ll}{g}_t^{r}f\left({\mathcal{H}}_t^r,{\Phi }^{\prime }\right)+{\mathcal{H}}_t^r,& \text{ if }{g}_t^r>P_{\beta }\left(G^r\right)\\ {\mathcal{H}}_t^r,& \text{ otherwise }\end{array}$$

其中$P_{\beta }(G^r)$是递归步骤$r$中所有分数的$\beta$百分位阈值。

为了确保步骤间的连贯进展，我们采用分层过滤(hierarchical filtering)：只有在递归步骤$r$中被选中的令牌才能在$r+1$中被重新评估。这模拟了早期退出行为，同时从头开始学习。由于更深的层倾向于编码越来越抽象和稀疏的信息，这种机制仅为最需要的令牌优先分配计算。

讲解

🪧1.核心逻辑：“专家” 选 “令牌”，复杂的多算，简单的少算

• “专家选择路由” 的核心是：🚨把模型的每一次递归步骤（比如第 1 次、第 2 次、第 3 次递归）当成一个 “专家”，每个专家只挑选自己认为 “需要继续计算” 的令牌（top-k 令牌），让它们进入下一轮递归，其他令牌则停止计算。

• ”专家是什么？“：这里的“专家”不是真的人，而是模型的每一次递归步骤。比如，如果模型有3次递归（$N_r=3$），就有3个专家：

  • 专家1：负责第1次递归，判断哪些令牌需要进入第2次递归；
  • 专家2：负责第2次递归，判断哪些令牌需要进入第3次递归；
  • 专家3：负责第3次递归，完成最后计算。

• “偏好的top-k令牌”：每个专家会给当前所有令牌打分，只选分数最高的前k个（top-k）令牌“晋级”，让它们继续计算。

• 每个专家（第$r$次递归）会根据令牌的“隐藏状态（${\mathcal{H}}_t^r$）”和自己的“路由参数（${\theta }_r$）”，给每个令牌（$t$）打一个分数（$g_t^r$）。

  • 隐藏状态：可以理解为令牌经过前几次计算后的 “中间结果”（比如“量子”这个词的中间结果可能更复杂，“的”的中间结果更简单）；

  • 激活函数（$\mathcal{G}$，比如sigmoid）：把分数压缩到$0-1$之间，方便判断“是否需要继续”。

  • 举例：专家1给10个令牌打分，“量子”得0.9分（复杂，需要多算），“的”得0.2分（简单，不用多算）。

  • 每个专家会设定一个“及格线（阈值$P_{\beta }(G^r)$）”：比如取所有令牌分数的β百分位（比如β=80，即前20%的分数为及格线）。

  • 分数高于阈值的令牌：继续进入下一次递归，计算公式为${\mathcal{H}}_t^{r+1}=g_t^{r}f({\mathcal{H}}_t^r,{\Phi }^{\prime })+{\mathcal{H}}_t^r$（简单说，就是用共享参数${\Phi }^{\prime }$更新令牌的中间结果）；

  • 分数低于阈值的令牌：停止计算，中间结果保持不变（${\mathcal{H}}_t^{r+1}={\mathcal{H}}_t^r$）。

  • 举例：专家1的阈值是0.6，“量子”（0.9分）晋级，“的”（0.2分）停步。

• “层级过滤：只有前一步选中的令牌，才能进入下一步评估”

  • 这是关键规则：比如专家1选中的令牌，才能被专家2评估；专家2选中的，才能被专家3评估。

  • 作用：避免“已经被判定简单的令牌”反复被评估，确保计算资源只流向“越来越复杂”的令牌。

  • 举例：

    • 专家1从10个令牌中选3个晋级；
    • 专家2只评估这3个，再选2个晋级；
    • 专家3只评估这2个，完成最终计算。

  • 模型的深层（多次递归后）会处理更抽象的信息（比如“量子力学”的逻辑关系，而不是“的”的语法功能），这些信息更“稀疏”（只有少数复杂令牌需要）。

  • 专家选择路由正好契合这一点：让简单令牌早停，复杂令牌多算，把算力花在“刀刃上”。

• 总结：专家选择路由的核心价值

  • 第1轮（专家1）淘汰大部分简单令牌（比如小学毕业）；
  • 第2轮（专家2）再淘汰一部分（比如初中毕业）；
  • 第3轮（专家3）只留最复杂的令牌继续深造（比如高中毕业）。

  这种机制让模型不浪费算力在简单令牌上，同时确保复杂令牌得到足够计算，最终实现“低成本高效果”。

---

翻译

令牌选择路由（图2b）：与专家选择不同（在每个递归步骤做出令牌选择），令牌选择从一开始就使每个令牌致力于一整套递归块。形式上，给定隐藏状态$H_t^1$（在中间循环策略中，$H_t^1=h_t^1$），路由器通过专家计算非线性函数（softmax或sigmoid）：$g_t=G({\theta }_r^{\top }{H}_t^1)$，其中$g_t^j$表示专家 j ∈ { 1 , . . . , N r } j \in\{1,...,N_{r}\} j∈{1,...,Nr​}的路由分数。令牌被分配给专家$i=\arg {\max }_j{g}_t^j$（top-1门控），这对应于顺序应用$i$次递归。然后，隐藏状态递归更新为：

$${\mathcal{H}}_t^{r+1}=\{\begin{array}{ll}{g}_t^{r}f\left({\mathcal{H}}_t^r,{\Phi }^{\prime }\right)+{\mathcal{H}}_t^1,& \text{ if }r=i\\ g_t^{r}f\left({\mathcal{H}}_t^r,{\Phi }^{\prime }\right),& \text{ otherwise }\end{array}$$

为了在相同计算下比较路由策略，我们使专家选择的令牌分配预算与令牌选择的相匹配。具体而言，我们校准专家选择的令牌容量（即top-k），以匹配具有完美负载平衡的令牌选择路由的预期令牌分布。在完美平衡的令牌选择中，每个令牌被分配到递归深度 i ∈ { 1 , . . . , N r } i \in\{1,...,N_{r}\} i∈{1,...,Nr​}的概率相等，均为$1/N_r$。因此，递归步骤$s$处理令牌的比例为$(N_r-s+1)/N_r$。例如，当$N_r=3$时，递归步骤1、2和3分别处理$3/3,2/3,1/3$的令牌。因此，我们在专家选择路由的top-k选择中应用相同的分数分配（即，k在$N_r$个递归步骤中按$N_r/N_r,...,1/N_r$的顺序排列）。

讲解

Token-choice routing 是 MoR 中第二种动态分配计算的策略，核心特点是 “一开始就给每个令牌定好‘计算次数’”，和专家选择路由（每次递归选令牌）形成鲜明对比。

🪧核心区别：“一次定终身” vs “步步筛选”

• 专家选择路由（Expert-choice）：每个递归步骤（如第1、2、3次）都重新选令牌（比如第1次留10个，第2次留5个），像“闯关”，每关淘汰一批；
• 令牌选择路由（Token-choice）：从一开始就给每个令牌分配固定的递归次数（比如“量子”算3次，“的”算1次），之后按这个次数执行，像“一开始就定好作业量”，不中途改。

🪧具体操作步骤（带例子，假设$N_r=3$ 次递归）

1. 第一步：初始打分，定好每个令牌的“计算次数”

• 当令牌刚进入模型（拿到初始隐藏状态${\mathcal{H}}_t^1$，比如“量子”的初始处理结果），路由器就给它“算命”：用非线性函数（如 softmax）计算对每个“专家”（即递归次数1、2、3）的分数 $g_t^j$（$j=1,2,3$）。
• 选分数最高的专家$i=\arg {\max }_j{g}_t^j$（top-1门控），这个 (i) 就是该令牌的总递归次数。
  • 例子：“量子”对专家3的分数最高（$i=3$）→ 要算3次；“的”对专家1的分数最高（$i=1$）→ 只算1次。

2. 第二步：按分配的次数递归计算，更新隐藏状态

拿到分配的次数$i$ 后，令牌开始按递归步骤（$r=1,2,...,N_r$）计算，隐藏状态更新规则分两种情况（公式2.2）：

• 如果当前递归步骤$r=i$（达到分配的次数）：
  ${\mathcal{H}}_t^{r+1}=g_t^{r}f({\mathcal{H}}_t^r,{\Phi }^{\prime })+{\mathcal{H}}_t^1$
  通俗说：用共享参数 (\Phi’) 计算后，还要“加回初始隐藏状态”，相当于“完成最后一步，整合结果”。

  • 例子：“量子”在$r=3$时（$r=i=3$），计算后加回初始状态 ${\mathcal{H}}_t^1$，完成最终更新。

• 如果当前递归步骤 $r\ne i$（还没到分配的次数）：
  ${\mathcal{H}}_t^{r+1}=g_t^{r}f({\mathcal{H}}_t^r,{\Phi }^{\prime })$
  通俗说：只用共享参数 ${\Phi }^{\prime }$ 更新，继续累积计算，不急于整合。

  • 例子：“量子”在$r=1$ 和$r=2$时（$r\ne 3$），只做中间更新，不回头加初始状态。

🪧和专家选择路由的对比（表格核心信息）

维度	令牌选择路由（Token-choice）	专家选择路由（Expert-choice）
优点	无信息泄露（No leakage）：因为次数从一开始定好，不会因后续步骤“偷看”信息导致偏差	计算预算固定（Static compute budget）：每步选多少令牌可控，总计算量稳定
缺点	负载不平衡（Load imbalance）：可能某几次递归令牌太多（比如都选3次），某几次太少	因果性问题（Causality violation）：后续步骤选令牌可能受“未来信息”影响
解决方法	平衡损失（Bal Loss）、无损失调整（Loss-free）：强制令牌均匀分配到各次数	辅助路由（Aux Rout）、辅助损失（Aux Loss）：修正因果偏差

🪧为什么要“校准计算预算”？

为了公平对比两种路由策略，需要让它们的总计算量相同：

• 假设 $N_r=3$，在“完美负载平衡”的令牌选择路由中，每个令牌被分配到1、2、3次递归的概率各为1/3。因此：
  • 第1次递归要处理所有令牌（3/3）；
  • 第2次递归处理分配次数≥2的令牌（2/3）；
  • 第3次递归处理分配次数=3的令牌（1/3）。
• 专家选择路由会按同样比例设置“每步选多少令牌”（比如第1步选3/3，第2步选2/3），确保两者计算量一致。

🪧总结：令牌选择路由的核心价值

它像“提前布置作业”：开学就告诉每个学生要做1次、2次还是3次作业，之后按计划完成，避免了“临时改作业量”的麻烦（无信息泄露），但需要想办法让“每次作业的学生数量”更均匀（解决负载不平衡）。这种策略和专家选择路由互补，共同支撑MoR的“动态计算”能力。

翻译

优势和局限性（表2-左）：尽管专家选择路由通过静态top-k选择保证了完美的负载平衡，但它存在信息泄露问题。训练期间的这种因果关系违反迫使我们使用辅助路由器或正则化损失，旨在在推理时准确检测top-k令牌，而无需访问未来的令牌信息。同时，令牌选择没有这种泄露，但由于其固有的负载平衡挑战，通常需要平衡损失或无损失算法。我们在第4.2节中更详细地探讨了MoR的这些组件。

2.2.2. 键值缓存策略：递归级缓存与递归共享

翻译

动态深度模型在自回归解码期间经常面临键值缓存一致性问题。当一个令牌提前退出时，其在更深层中对应的键和值将缺失，而这些可能是后续令牌的关键信息。一些方法尝试重用陈旧的条目或运行并行解码，但这些解决方案仍然引入了开销和复杂性。为此，我们设计并探索了两种专为MoR模型定制的键值缓存策略：递归级缓存和递归共享。

递归级键值缓存（recursion-wise KV caching)（图2c-上）：受Raposo等人（2024）启发，我们选择性地缓存键值对：只有被路由到特定递归步骤的令牌才在该级别存储其键值条目。因此，每个递归深度的键值缓存大小由专家选择中的容量因子或令牌选择中的实际平衡比率决定。然后，注意力被限制在那些本地缓存的令牌上。这种设计促进了块本地计算，提高了内存效率并减少了IO需求。

递归键值共享（Recursive KV sharing.）（图2c-下）：我们MoR模型的一个关键设计选择是所有令牌至少经过第一个递归块（见注释3）。我们利用这一点，专门在这个初始步骤缓存键值对，并在所有后续递归中重用它们。因此，查询长度可能会根据选择容量在每个递归深度缩短，但键和值的长度将始终保持完整序列。这确保了所有令牌都可以访问过去的上下文而无需重新计算，尽管存在任何分布不匹配。

优势和局限性（表2-右）：递归级缓存将整个模型的键值内存和IO减少到大约$(N_r+1)/(2N_r)$倍（假设容量因子遵循在$N_r$个递归步骤上如$N_r/N_r,...,1/N_r$的序列）。它还将每层注意力FLOPs减少到普通模型的$(k/N_{ctx}{)}^2$倍，从而显著提高了训练和推理阶段的效率。同时，递归共享通过全局重用上下文可以产生最大的内存节省。具体而言，通过在共享深度跳过键值投影和预填充操作，可以实现显著的加速（Sun等人，2024）。然而，注意力FLOPs仅减少$k/N_{ctx}$倍，并且大量的键值IO仍然导致解码瓶颈。

注3：尽管这并非MoR框架本身的严格要求。

讲解

🚨先搞懂背景：动态深度模型的 “KV 缓存难题”

在动态深度模型（如 MoR）中，每个令牌可能提前退出计算（比如简单词只算 1 次，复杂词算 3 次）。但问题是：

• 提前退出的令牌，在更深的递归步骤中没有对应的 KV 对（中间结果），而后续令牌可能需要参考这些信息

  • 举个例子：拆解：“这”“篇”“论文”“讨论”“的”“是”“量子”“力学”“的”“基础”“原理”“。”
  • “讨论的是量子力学” 中，“的” 连接 “讨论” 和 “量子力学”，明确 “量子力学” 是 “讨论” 的对象；
  • 如果 “的” 提前退出后，模型丢失了它的 KV 对（中间结果），“量子” 在后续计算中可能无法正确关联 “讨论” 和 “量子力学” 的关系，导致理解偏差（比如误判为 “讨论是量子力学”）。

• 之前的解决方法（如复用旧 KV 对、并行解码）要么效率低，要么太复杂。

  • 复用旧 KV 对

    • 实现逻辑：当令牌提前退出后， deeper 层（后续递归）若需要它的 KV 对，直接复用该令牌在浅层（如第 1 次递归）的旧 KV 对，而不重新计算。
    • 问题：效率低
      • 旧 KV 对是令牌在浅层的 “初步结果”，可能无法反映 deeper 层需要的抽象信息（比如 “的” 在第 1 层的 KV 对只包含语法信息，而 deeper 层可能需要它与 “量子” 的语义关联）。
      • 复用旧信息可能导致推理精度下降，相当于 “用小学笔记解大学题”，为了节省计算牺牲了准确性。

  • 并行解码

    • 实现逻辑：为不同退出深度的令牌设计独立的解码路径，同时处理 “已退出的令牌” 和 “仍活跃的令牌”，确保所有 KV 对都能被访问。
    • 问题：复杂度高
      • 需要额外设计并行计算框架，协调不同路径的令牌状态（比如跟踪哪些令牌在第 1 层退出，哪些在第 3 层活跃）。
      • 工程实现复杂，且并行路径会增加内存占用和调度开销（比如 GPU 需要同时维护多组 KV 缓存），反而可能降低整体效率。

因此，MoR 专门设计了两种 KV 缓存策略，既保证信息完整，又不浪费资源。

🪧策略 1：Recursion-wise Caching（按递归缓存）——“按需记笔记，只留当前用的”

• 核心逻辑：只给 “当前递归步骤中仍活跃的令牌” 存储 KV 对，其他令牌的 KV 对不缓存。

• 类比：：就像学生做小组作业，每次讨论（递归步骤）只记 “当前参与讨论的人” 的笔记（KV 对），提前离开的人（退出的令牌）的笔记不记在当前讨论的本子上。

• 具体操作：

  • 令牌被路由到第 r 次递归时，才在第 r 层存储它的 KV 对；未被路由到的令牌，该层不存。
  • 注意力计算只在 “当前层缓存的令牌” 之间进行（比如第 2 次递归只算还活跃的 5 个令牌的关联）。

• 效果

  • 内存效率高：KV 缓存大小随递归深度减少（比如 3 次递归，缓存大小依次为 10→5→2），整体内存和 IO 减少到约$(N_r+1)/(2N_r)$倍（假设递归次数为$N_r$）
  • 计算量低：每层注意力的 FLOPs（计算量）减少到传统模型的$(k/N_{ctx}{)}^2$（（k 是当前活跃令牌数，$N_{ctx}$是总令牌数），训练和推理都更快。

🪧策略2：Recursive KV Sharing（递归共享）——“一次记全笔记，反复用”

• 核心逻辑：所有令牌至少经过第 1 次递归，因此只在第 1 次递归时缓存所有令牌的 KV 对，后续递归直接复用这组 KV 对，不再重新计算。

• 类比：小组作业第一天所有人都到场，记一份完整的笔记（第 1 次递归的 KV 对），之后哪怕有人离开，后续讨论都直接用这份笔记，不再重新记录。

• 具体操作：

  • 第 1 次递归：缓存所有令牌的 KV 对（完整序列）
  • 第 2、3 次递归：复用第 1 次的 KV 对，不重新生成。此时 “查询（Query）” 的长度可能减少（只剩活跃令牌），但 “键（Key）” 和 “值（Value）” 的长度始终是完整序列（包含所有令牌）。

• 效果：

  • 最大内存节省：全局复用 KV 对，跳过后续递归的 KV 投影和预填充操作（Sun et al., 2024），大幅提速。
  • 信息完整：即使令牌提前退出，也能通过复用的 KV 对访问所有历史上下文，避免信息缺失。

• 两种策略的优缺点对比

维度	按递归缓存（Recursion-wise Caching）	递归共享（Recursive KV Sharing）
内存效率	高：KV大小随递归深度减少，整体内存减到约( Nr +1 )/(2Nr)倍	更高：只存1次完整KV，全局复用，节省最多
注意力计算量	低：FLOPs减少到( k/Nctx )²（平方级减少）	中等：FLOPs减少到k/Nctx（线性减少）
IO开销	低：只读写当前层活跃令牌的KV，IO少	高：需频繁读写完整KV序列，可能成瓶颈
信息完整性	仅保证当前活跃令牌的上下文，适合高效计算	保证所有令牌的完整上下文，适合复杂推理

总结：两种策略的核心价值

MoR通过这两种策略，解决了动态深度模型的“KV缓存困境”：

• 按递归缓存像“精简笔记”，适合追求极致效率的场景（内存少、计算快）；
• 递归共享像“万能笔记”，适合需要完整上下文的场景（信息全、但IO稍高）。

两者结合，让MoR在“高效计算”和“信息完整”之间找到了平衡，这也是它优于传统模型的关键之一。

参考

• 「有望成为Transformer杀手」，谷歌DeepMind新架构MoR实现两倍推理速度