[陀螺仪底层到应用]-------学习草稿

问题描述

刚开始我的IMU放置是IMU坐标系初始位置和刚体在大地中的坐标系一致，即IMU的X对应刚体X，IMU的Y轴对应刚体Y轴，IMU的Z轴对应刚体Z轴,后来我改变了IMU相对于刚体的位置，IMUX轴对应刚体Z轴，IMU的Z轴对应刚体X轴反方向，我的姿态解算过程是IMU的角速度–>四元数+IMU的加速度==互补滤波之后得到欧拉角，这样解算出的姿态被影响，如何避免这种影响

当你改变了IMU相对于刚体的位置时，需要重新定义IMU坐标系相对于刚体坐标系的旋转矩阵或四元数，然后在姿态解算中使用这个新的旋转矩阵或四元数来转换加速度和角速度的数据。如果你仍然使用原来的旋转矩阵或四元数，那么你会得到错误的姿态解算结果。

当我改变了IMU相对于刚体的位置时，如何重新定义IMU坐标系相对于刚体坐标系的旋转矩阵或四元数在姿态解算中使用这个新的旋转矩阵或四元数来转换加速度和角速度的数据

当你改变IMU相对于刚体的位置时，需要重新定义IMU坐标系相对于刚体坐标系的旋转矩阵或四元数，以便在姿态解算中使用这个新的旋转矩阵或四元数来转换加速度和角速度的数据。以下是一些步骤：

确定新的IMU坐标系和刚体坐标系之间的旋转关系。你可以通过将IMU相对于刚体的旋转角度或旋转矩阵记录下来，或通过传感器数据进行估算。

使用旋转角度或旋转矩阵来计算新的旋转四元数。这可以通过旋转矩阵转换到四元数，或者通过欧拉角转换到四元数的公式来完成。

在姿态解算中使用新的旋转四元数来转换加速度和角速度的数据。你可以将加速度和角速度的数据转换到刚体坐标系中，然后使用相同的姿态解算方法来计算新的姿态。

需要注意的是，重新定义IMU坐标系相对于刚体坐标系的旋转矩阵或四元数，会影响姿态解算的准确性。因此，在重新定义旋转矩阵或四元数后，需要进行适当的校准和调整，以确保姿态解算的准确性。

另外，如果你使用的是互补滤波算法来解算姿态，那么你需要调整滤波算法的参数，使其适应新的IMU相对于刚体的位置。这是因为互补滤波算法中使用的加速度和角速度数据在不同的IMU相对于刚体的位置下会有不同的响应。你需要重新校准滤波算法的参数，以便正确地解算出姿态。

最后，还需要注意在实际应用中，IMU相对于刚体的位置的改变可能会引入误差，导致姿态解算的精度下降。因此，如果可能的话，最好将IMU放置在刚体的中心位置，以减少这种误差。

陀螺仪能获取的数据

角速度

加速度

磁力计数据（部分九轴陀螺仪有）

四元数

1. 【四元数的可视化】 https://www.bilibili.com/video/BV1SW411y7W1/?share_source=copy_web&vd_source=f0275a32ba5b5daa7fb5597581dccb20
2. https://github.com/CatOnly/CrashNotes/tree/master/LinearAlgebra总结
3. 四元数和旋转(Quaternion & rotation) - lxycg的文章 - 知乎
   https://zhuanlan.zhihu.com/p/78987582
4. https://eater.net/quaternions/

• 复数是实数的二维延申，四元数是复数的四维延伸
• 应用到图像，机器人，量子力学，三维旋转（最高效，避免误差）
• 四元数所描述的是对四维空间的特殊作用
• 2.23+232i+2.23j+32k四元数中i,j,k轴相互垂直，并且都与实数轴垂直
• 有分配性，没有可交换性

四元数的乘法

四元数表示空间旋转

相对于欧拉角的好处是，欧拉角有一个万向节锁死的问题，而且四元数计算效率更高

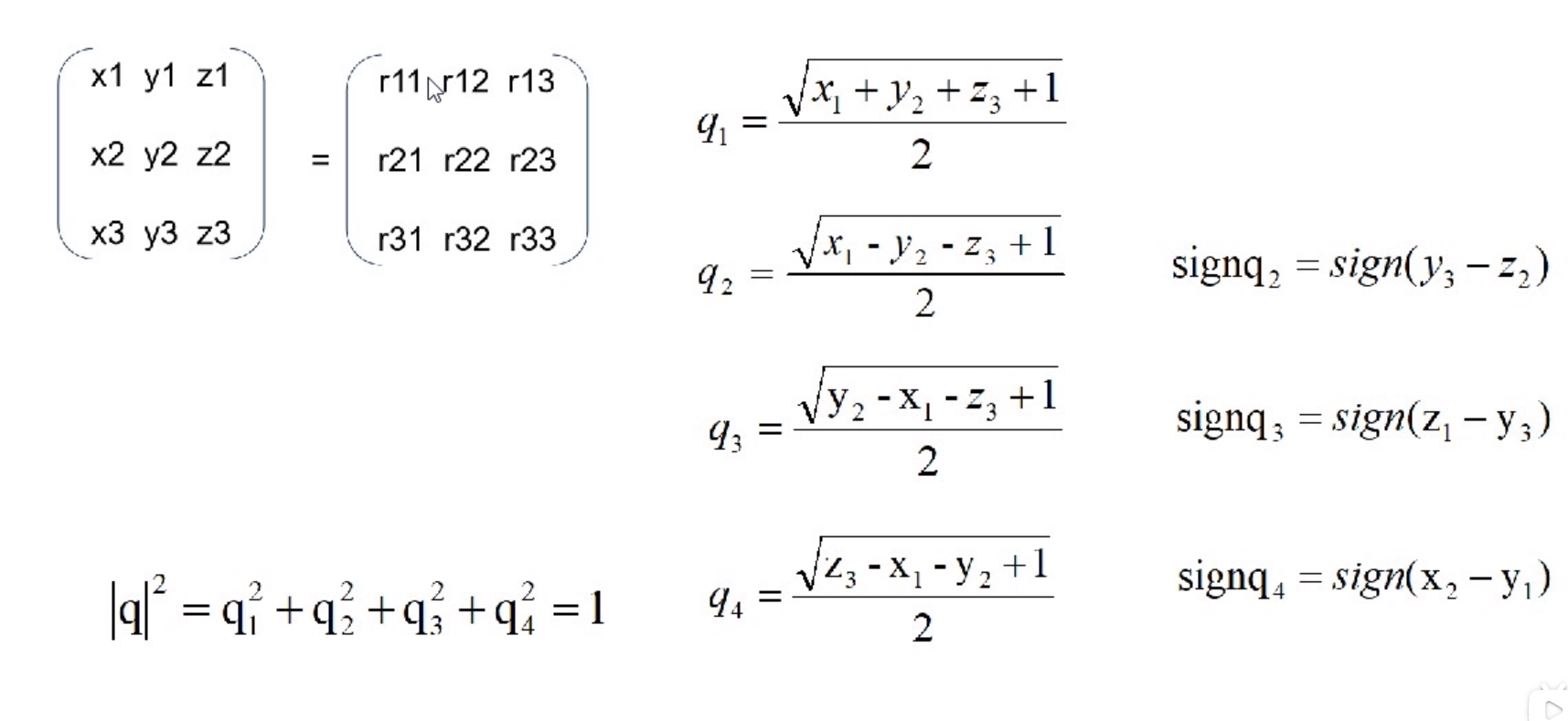
四元数与欧拉角的转换

1. https://en.wikipedia.org/wiki/Conversion_between_quaternions_and_Euler_angles四元数和欧拉角之间的转换
   

四元数与欧拉角的转化

干货整理：欧拉角、旋转矩阵、四元数合辑https://zhuanlan.zhihu.com/p/79894982

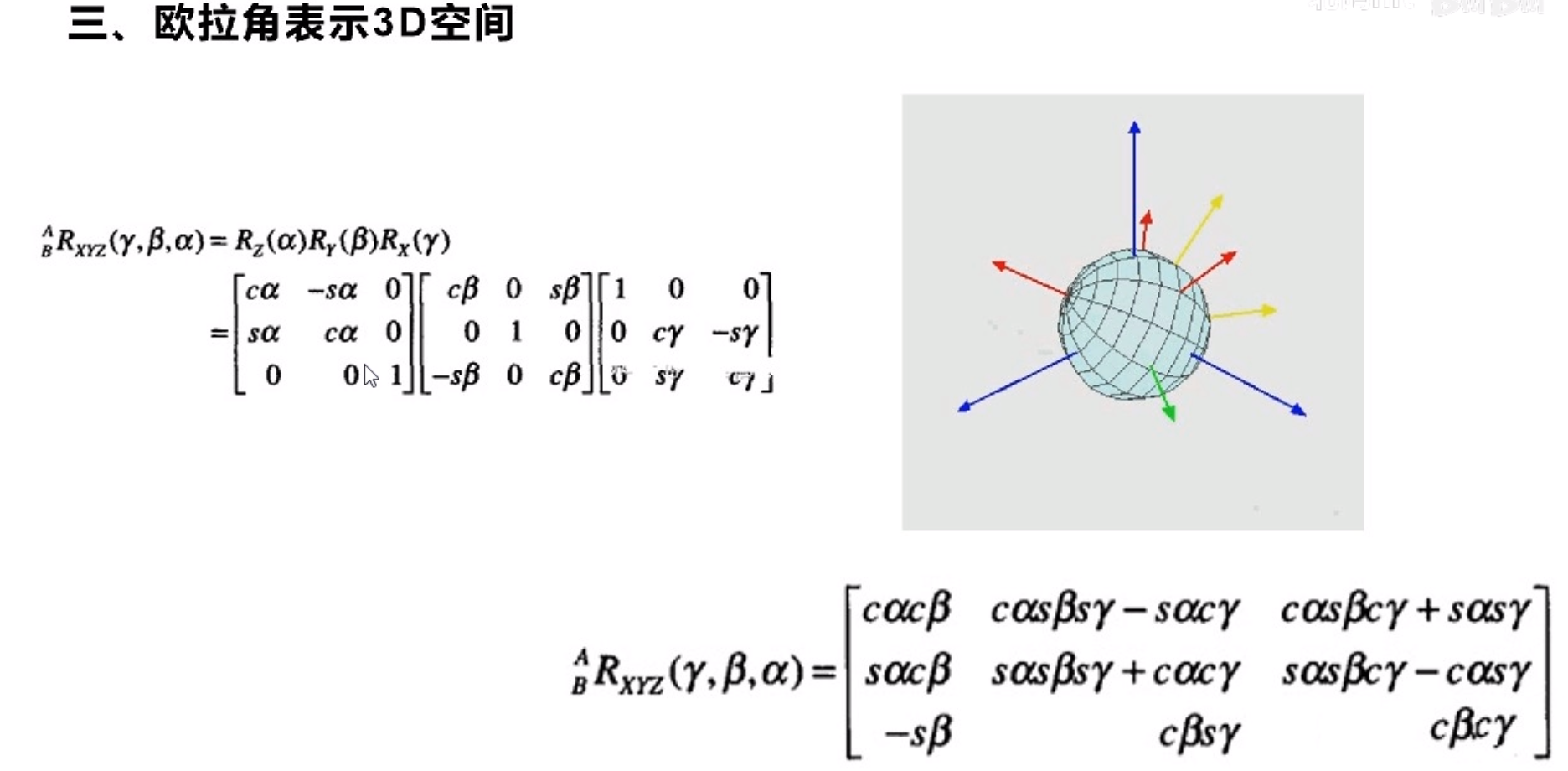
欧拉角表示3D空间

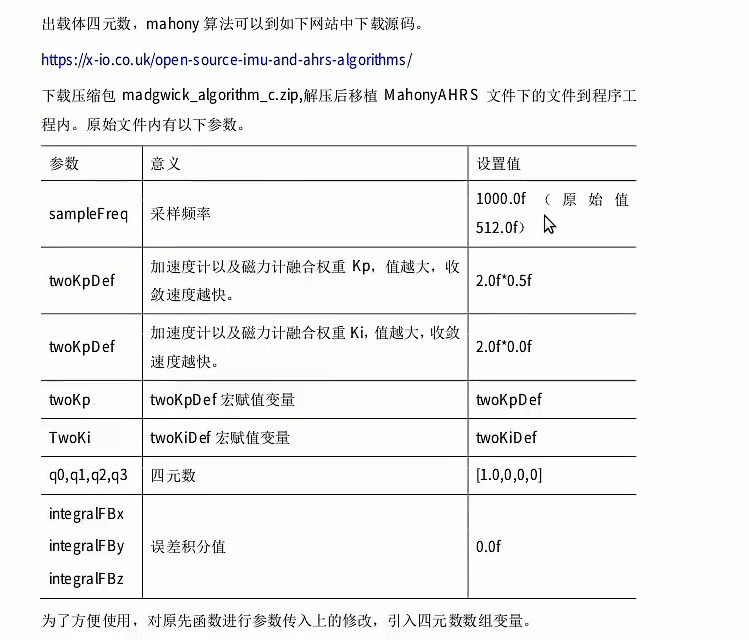
mahony算法移植

http://t.csdn.cn/qaIYY写的非常好！！！！！
mlahony算法是常见的姿态融合算法，将加速度计，磁力计，陀螺仪共九轴数据，融合解算

欧拉角旋转顺序

欧拉角旋转顺序不一样最终导致四元数转换为欧拉角的公式也不一样

四元数姿态解算----扩展卡尔曼滤波器设计

【四元数姿态解算----扩展卡尔曼滤波器设计】 https://www.bilibili.com/video/BV1Hf4y1D75M/?share_source=copy_web&vd_source=a5058e7a9022325237e9d20af2d2a2de
为加速度计、陀螺仪和磁力计融合设计基于四元数的 EKF https://mwrona.com/posts/attitude-ekf/

陀螺仪温度补偿

https://www.hindawi.com/journals/mpe/2021/1636001/一种基于LSTM-RNN的光纤陀螺仪漂移补偿
温度漂移等噪声会降低FOG的精度，从而影响IMU的分辨率精度。为了减小雾漂移，提高导航精度，建立长短期记忆循环神经网络（LSTM-RNN）模型，提出一种基于移动平均的温度变化率实时采集方法。