网络流 FF算法简析

$FF$（$Ford-Fulkerson$）算法，用于求从源点到汇点的最大可行流（以下简称最大流）问题的算法。

求解最大流问题的算法很多，FF是最拉胯的那一档（）。

属于增广路类算法，主要思想就是通过增广路对于现有网络流不断改进求出最优。

令$f[e]$表示边的流量，$c[e]$表示容量，对于一个可行流必有$f[e]<=c[e]$（不然就溢出了）

首先我们很容易想出一个正确性未知的算法：

每次从$s$到$t$的路径中选出一条所有边上的$f[e]$都$<c[e]$，那么这条边上一定可以再多一些流量，答案就可以加上最小的$c[e]-f[e]$，且每条边的流量加上这个值。

但是这个在实际操作中就会发现：有些不对啊~

举个例子：

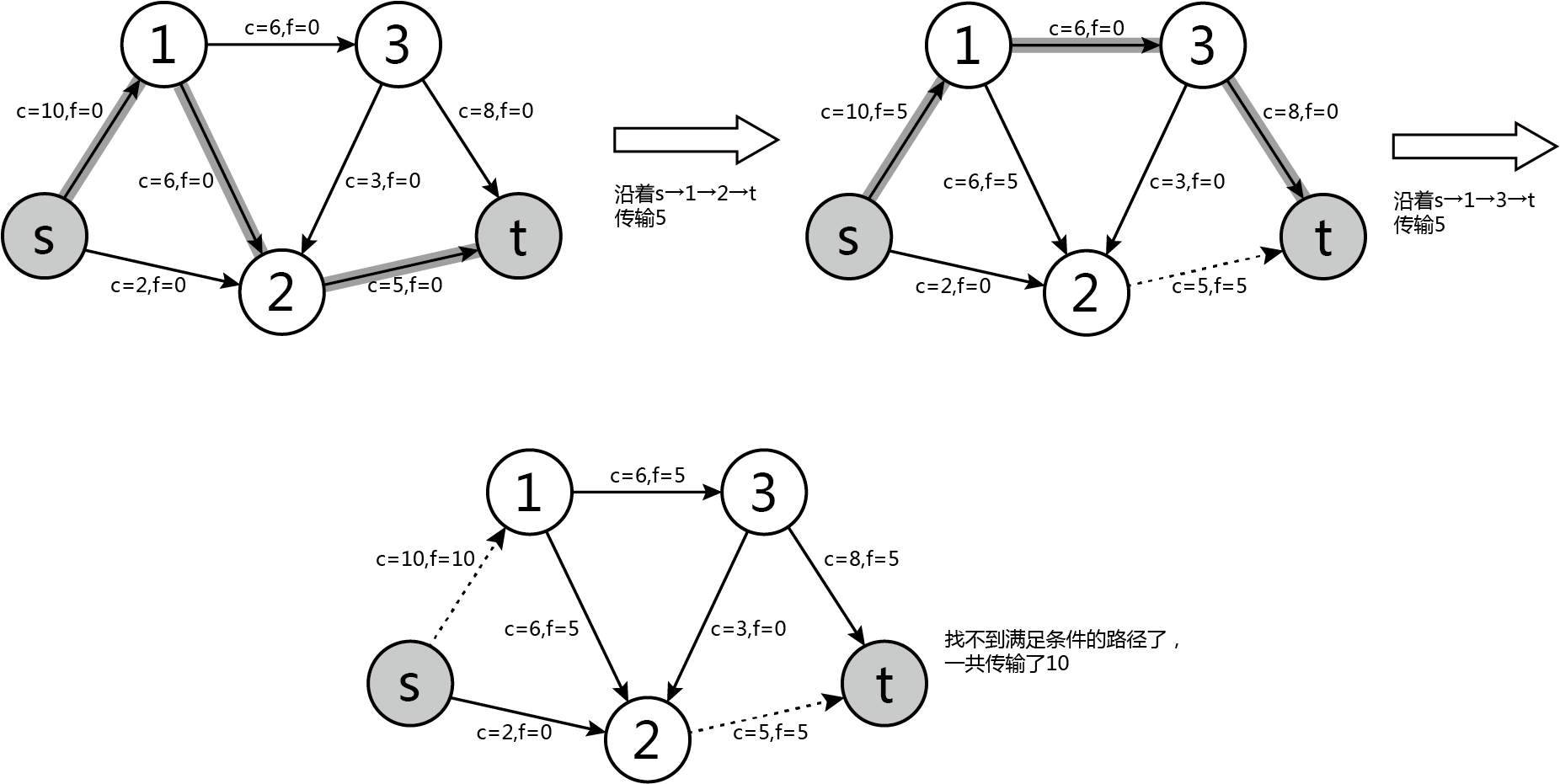
然而这张图的最大流可以达到11。

如果我们在某些决策上可以进行返回那么是不是就可以保证答案最优了呢？
在上述例子中，如果将$1—2$的流退回去，得到新的流：$s—2—1—3—t$，就可以得到最优结果。

所以我们新加入一类边：反向边。对正向边的操作反向操作在反向边上。

改进操作就是在寻找路径时不仅局限于$f[e]<c[e]$，还可以加入反向边的$f[e]>0$的边起到反悔的作用。

这就是FF算法了。