快速排序的使用

快速排序

问题
利用快速排序将以下数组从小到大进行排序：
输入：
{10,1,12,78,68,15,34,900,23,18}
输出：
{1,10,12,15,18,23,34,68,78,900}

快速排序的理解分析：
快速排序是冒泡排序的改进。是一种分段的思想。通过多次的比较和交换实现最后排序的结果。
关于题目示例的排序解析如下。
PS：快速排序是一种基本的方法，可以用来进行多方面的拓展，作为其他问题需要进行排序时可以使用到，时间复杂度会降低。

代码实现：

（以下代码均为C语言进行实现）

（1）i指向初始数，j指向最后一个数的后面一个。最后交换的数是以j为主导。先从左右开始寻找没有差别，不会出错。

void swap(int &a,int &b)
{
	int t = a;
	a=b;
	b=t;
}
//主函数输入的r=len-1
void partition(int a[],int p,int r)
{
	if(p>=r){
		return;
	}
	int i=p;
	int j=r+1;
	int x=a[p];//基准数 
	//保证x左边的数比x小，x右边的数比右边小 
	while(true)
	{
		while(a[++i]<x&&i<r);
		while(a[--j]>x);
		if(i>=j) break;
		swap(a[i],a[j]);
	}
	
	a[p]=a[j];
	a[j]=x;
	//分区 
	partition(a,p,j-1);
	partition(a,j+1,r);
}

或者可以将分段函数分开。（记得主函数是在调用qk函数）

void swap(int &a,int &b)
{
	int t=a;
	a=b;
	b=t;
}

int partition(int a[],int p,int r)
{
	int i=p;
	int j=r+1;
	int x=a[p];
	while(true)
	{
		while(a[++i]<x&&i<r);
		while(a[--j]>x);
		if(i>=j)break;
		swap(a[i],a[j]);
	}
	a[p]=a[j];
	a[j]=x;
	return j;
}

void qk(int a[],int p,int r)
{
	if(p>=r)
	{
		return;
	}
	int j=partition(a,p,r);
	qk(a,p,(j-1));
	qk(a,(j+1),r);
}

（2）i与j指向的位置不同，且分区内最后交换的数，也是不同。
i指向第一个数，j指向最后一个数；且最后的交换是以i为主导。
且一定要先从右边开始找比基准数小的数与后面找出来的比基准数大的数进行交换。

void partition(int a[], int p, int r)
{
	if(p>=r)
	{
		return;
	}
	int i=p;
	int j=r;
	int x=a[p];//基准数
	while(true)
	{
		while(a[i]<=x&&i<j)
		{
			i++;
		}
		while(a[j]>=x&&i<j)
		{
			j--;
		}	
		if(i>=j) break;	
		int temp=a[i];
		a[i]=a[j];
		a[j]=temp;
	 } 
	 a[p]=a[i];
	 a[i]=x;
	 partition(a,p,i-1);
	 partition(a,i+1,r);
}

#include <stdio.h>
int partition(int a[], int p, int r)
{
	int i=p;
	int j=r;
	int x=a[p];//基准数
	while(true)
	{
		while(a[j]>=x&&i<j)
		{
			j--;
		}
		while(a[i]<=x&&i<j)
		{
			i++;
		}
		
		if(i>=j) break;		
		int temp=a[i];
		a[i]=a[j];
		a[j]=temp;
	 } 
	 a[p]=a[i];
	 a[i]=x;
	 return i;
}

void qk(int a[],int p,int r)
{
	if(p>=r)
	{
		return;
	}
	int i=partition(a,p,r);
	qk(a,p,(i-1));
	qk(a,(i+1),r);
}

int main(void)
{
	int a[10]={10,1,12,78,68,15,34,900,23,18};
	qk(a,0,9);
	printf("{");
	for(int i=0;i<9;i++)
	{
		printf("%d,",a[i]);
	}
	printf("%d}",a[9]);
}

运行结果截图均如下：

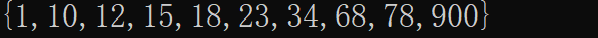
总结

以上的快速排序内容，是我个人综合上课内容和各种网上解法之后总结出来的一些规律，和一些需要注意到的细节问题，不过大都是因为自己学艺不精然后会犯的错误。而且还有一些地方可能还是有模棱两可的理解错误，如果后面我有新的理解和收获会进行修缮。
如果有什么问题，希望各位大佬知道，我会继续努力学习新的知识，蟹蟹！！！