十大排序算法——3种归并排序

归并排序

• 典型的分治思想

• 递归排序算法：先递归地将其分成两半分别排序，然后将结果归并起来。

• 时间上（优）：能保证长度为N的数组排序所需时间和NlogN成正比，就能将一个庞大的数组排序，可以处理数百万甚至更大规模的数组。（这是插入排序或选择排序做不到的）

• 空间上（劣）：所需的额外空间和N成正比。

• 归并排序是一种渐进最优的基于比较排序的算法

1. 原地归并的抽象方法

思想：将子数组a[lo…mid]和a[mid+1…hi]归并成一个有序的数组并将结果存放在a[lo…hi]中。它将涉及的所有元素复制到一个辅助数组中，再把归并的结果放回原数组。

private static Comparable[] aux; //归并所需的辅助数组

public static void merge(Comparable[] a,int lo,int mid,int hi){
    //将a[lo..mid]和a[mid+1..hi]归并
    aux = new Comparable[a.length];
    int i = lo, j = mid+1;

    for (int k=lo; k<=hi; k++) //将a[lo..hi]复制到aux[lo..hi]
        aux[k] = a[k];
    for (int k=lo; k<=hi; k++){//归并回到a[lo..hi]
        //其中一侧全部放入a后，将另一侧剩下的也全部放入
        if (i>mid) a[k]=aux[j++];
        else if (j>hi) a[k]=aux[i++];
        //前期在比较左右两边哪侧的小，小的放入a并将指针前进
        else if (aux[j].compareTo(aux[i])<0) a[k]=aux[j++];
        else a[k]=aux[i++];
    }
}

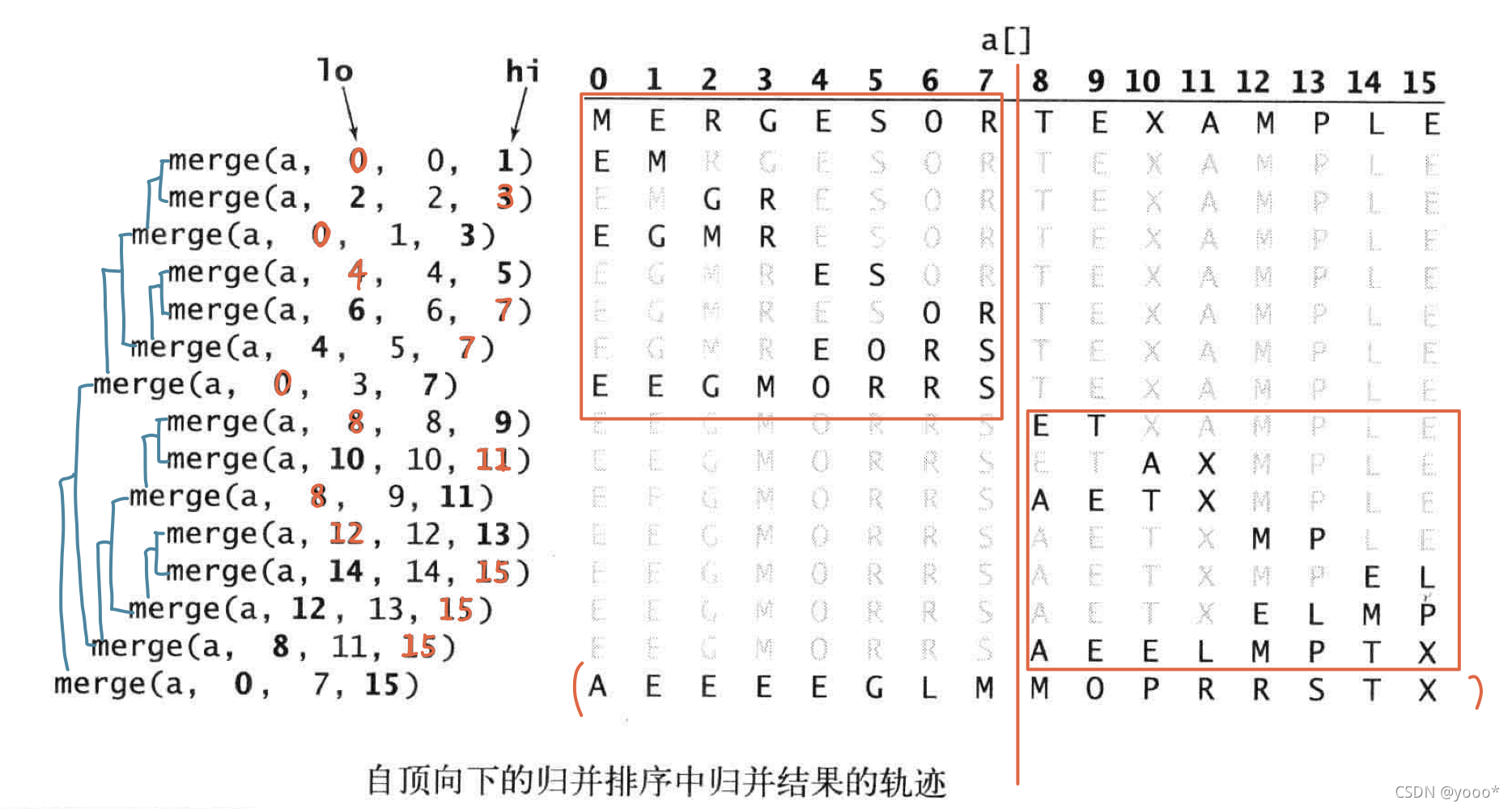
2.自顶向下的归并排序

思想：将数组元素不断二分，直到子数组的元素个数为1个，而后进行合并，直到合成一个有序的数组。

• 对于长度为N的任意数组，自顶向下的归并排序需要(1/2)NlogN~NlogN次比较
• 对于长度为N的任意数组，自顶向下的归并排序最多需要访问数组6NlogN次

public static void mergeUB(Comparable[] a){
    aux = new Comparable[a.length]; //一次性分配空间
    sort1(a,0,a.length-1);
}

private static void sort1(Comparable[] a,int lo,int hi){
    //将数组a[lo..hi]排序
    if (hi<=lo) return; //若只有一个元素
    int mid = (lo+hi)/2;
    sort1(a,lo,mid); //将左半边排序
    sort1(a,mid+1,hi); //将右半边排序
    merge(a,lo,mid,hi); //归并
}

3.自底向上的归并排序

思想：两两归并->四四归并->八八归并->…在每一轮归并中，最后一次归并的第二个子数组可能比第一个子数组要小，但这对merge()方法不是问题。

同自顶向下归并：

• 对于长度为N的任意数组，自底向上的归并排序需要(1/2)NlogN~NlogN次比较
• 对于长度为N的任意数组，自底向上的归并排序最多需要访问数组6NlogN次

public static void mergeBU(Comparable[] a){
    int N = a.length;
    for (int sz=1; sz<N; sz*=2) //sz子数组大小，翻倍
        for (int lo=0; lo<N-sz; lo+=sz+sz) //lo子数组索引，向后移动
            merge(a,lo,lo+sz-1,Math.min(lo+sz+sz-1,N-1)); //考虑归并的最后一组的大小可能比sz小
}

---

比较自顶向下和自底向上归并：

• 当数组长度为2的幂时，自顶向下和自底向上的归并排序比较次数和数组访问次数正好相同，只是顺序不同
• 自底向上更适合链表组织的数据：想象一下将链表先大小为1的子链表进行排序，然后是2,4…这种方法只需要重新组织链表的链接就能将链表原地排序。