#32 Longest Valid Parentheses

最新推荐文章于 2022-09-01 00:56:47 发布

原创最新推荐文章于 2022-09-01 00:56:47 发布 · 112 阅读

0 ·

CC 4.0 BY-SA版权

leetcode 专栏收录该内容

188 篇文章

订阅专栏

本文深入探讨了寻找最长有效括号子串的三种高效算法：动态规划、使用堆栈和迭代删除。通过实例解析，展示了每种方法的实现细节及优劣对比，帮助读者理解并掌握这一经典字符串处理问题。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

Description

Given a string containing just the characters ‘(’ and ‘)’, find the length of the longest valid (well-formed) parentheses substring.

Examples

Example 1:

Input: “(()”
Output: 2
Explanation: The longest valid parentheses substring is “()”

Example 2:

Input: “)()())”
Output: 4
Explanation: The longest valid parentheses substring is “()()”

解题思路

先说自己的，其实一开始想用动态规划，但是规则想不太出来所以放弃了，用的方法和后面的Stack方法有些类似，但时间复杂度要多一点orz
以 ( ( ( ) ) ( ) ( ) ) ) 为例

首先将它的index都存在一个ArrayList中
然后循环遍历ArrayList中的所有index，检查相邻的两个字符，找到形如 “()” 的substring，然后将他们的index从ArrayList中删去
( ( ) ) )
再次重复循环ArrayList，直到没有可删除的substring为止
这样的ArrayList中的数值代表的含义如下：
假设arr = [2, 8, 12]，则意味着 0 - 1，3 - 7， 9 - 11为合法substring
最后在ArrayList的0号位置插入 -1，在末位插入String的长度，补全整个区间
则计算整个ArrayList相邻两个数之间的差值，然后找到最大的即可

class Solution {
    public int longestValidParentheses(String s) {
        Map<Integer, Character> m = new LinkedHashMap<>();
        List<Integer> remain_num = new ArrayList<>();
        int i;
        for(i = 0; i < s.length(); i++){
            remain_num.add(i);
            m.put(i, s.charAt(i));
        }
        Boolean flag = true;
        while(flag){
            flag = false;
            for(i = 0; i < remain_num.size() - 1; i++){
                if(m.get(remain_num.get(i)) == '(' && m.get(remain_num.get(i+ 1)) == ')'){
                    remain_num.remove(i);
                    remain_num.remove(i);
                    i--;
                    flag = true;
                }
            }
        }
        remain_num.add(0, -1);
        remain_num.add(s.length());
        List<Integer> length = new ArrayList<>();
        for(i = 0; i < remain_num.size() - 1; i++)
            length.add(remain_num.get(i + 1) - remain_num.get(i) - 1);
        Collections.sort(length);
        return length.get(length.size() - 1);
    }
}

动态规划算法

那之后肯定会去摸solution嘿嘿，毕竟是hard，而且觉得动态规划一定能做只不过自己没想出来
嗯人家给的递推式还是很有道理的QuQ
先全部初始化为0，然后只在 “)” 的位置进行更新
$\left\{ \begin{array}{lcl} dp[i - 2] + 2 & & {当前字符和上一个字符组成（）}\\ dp[i - 1] + dp[i - dp[i - 1] - 2] + 2 & & {当前字符和上一个字符组成））且第i - dp[i - 1] - 1个字符为（}\\ \end{array} \right.$
第一个更新方式很好理解，就是在上一个的基础上加上长度2
第二个更新方式就妙在 $i - d p [i - 1] - 1$ 这个位置，因为上一个字符也是），然后以他为终极字符的最长substring长度为 $d p [i - 1]$ ，那它再上一级就是这个substring的前一个字符，如果这个字符是（，则意味着它们可以匹配成一对，这样整体长度就可以 + 2，至于更新规则中的 $d p [i - d p [i - 1] - 2]$ 则是因为如果后面的匹配成对了，就可以和前面的连成一串了
那找到这串数里面最大的就是最终结果啦

 public int longestValidParentheses(String s) {
        int maxans = 0;
        int dp[] = new int[s.length()];
        for (int i = 1; i < s.length(); i++) {
            if (s.charAt(i) == ')') {
                if (s.charAt(i - 1) == '(') {
                    dp[i] = (i >= 2 ? dp[i - 2] : 0) + 2;
                } else if (i - dp[i - 1] > 0 && s.charAt(i - dp[i - 1] - 1) == '(') {
                    dp[i] = dp[i - 1] + ((i - dp[i - 1]) >= 2 ? dp[i - dp[i - 1] - 2] : 0) + 2;
                }
                maxans = Math.max(maxans, dp[i]);
            }
        }
        return maxans;
    }
}

Stack

这是solution里面的另一种方法，其实基本思路和我的想法差不多，但是由于运用了堆栈的思想，所以只要过一遍字符串，就能得到结论，时间复杂度是O(n)
这里嫖一下leetcode的视频嘿嘿，还是比较清晰的
一开始先入栈 -1（和之间补全区间的意思一样

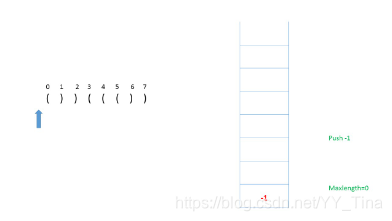
接下来依次判断，是（，所以将其的 index push入栈

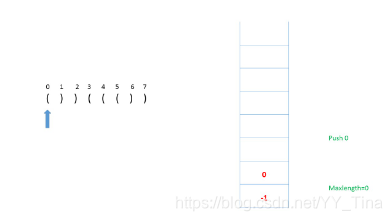
因为是），所以pop出栈内的值，更新当前length = index - pop_value

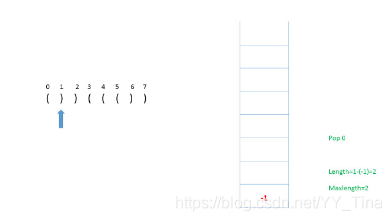
因为是），所以pop

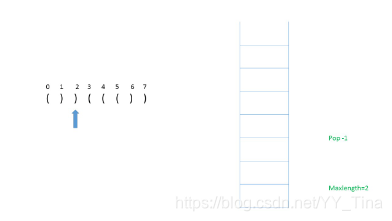
因为栈内空了，所以将）的index也push进去

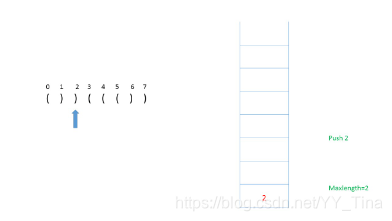
（，push

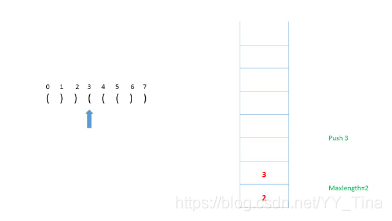
继续push

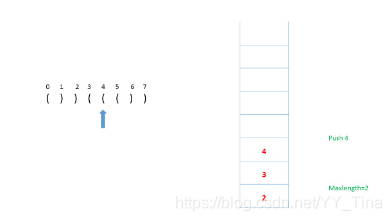
还push

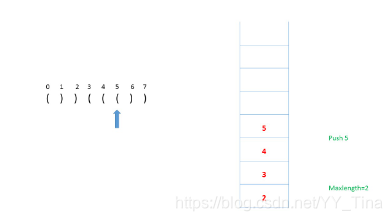
pop掉，更新length = index - top_value

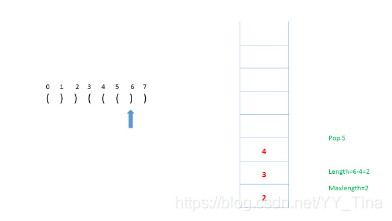
pop掉，更新 length = index - top_value
且发现比之前的max_length大，顺便更新max_length

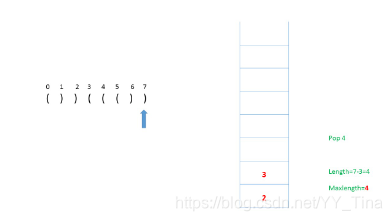
其他

CCF报名网站崩了hhhhhh