文章目录
最优化问题中的数学基础
导数
-
数学定义: \textbf{数学定义:} 数学定义: 设函数 y = f ( x ) y=f(x) y=f(x) 在点 x 0 x_0 x0 的某个邻域内有定义。则函数在 x 0 x_0 x0处的导数定义为 f ′ ( x 0 ) f'(x_0) f′(x0),其数学表达式为:
f ′ ( x 0 ) = lim Δ → 0 Δ y Δ x = lim Δ → 0 f ( x 0 + Δ x ) − f ( x 0 ) Δ x f'(x_0)= \lim_{\Delta \rightarrow 0} \frac{\Delta y}{\Delta x}= \lim_{\Delta \rightarrow 0} \frac{f(x_0+\Delta x)-f(x_0)}{\Delta x} f′(x0)=Δ→0limΔxΔy=Δ→0limΔxf(x0+Δx)−f(x0)
其中, Δ x \Delta x Δx为自变量 x x x在 x 0 x_0 x0 处的增量, Δ y \Delta y Δy为函数相应取得的增量. -
几何意义: \textbf{几何意义:} 几何意义: 函数 y = f ( x ) y = f(x) y=f(x) 在点 P ( x 0 , f ( x 0 ) ) P(x_0, f(x_0)) P(x0,f(x0)) 处的导数 f ′ ( x 0 ) f'(x_0) f′(x0) 的几何意义是:曲线 y = f ( x ) y = f(x) y=f(x) 在点 P ( x 0 , f ( x 0 ) ) P(x_0, f(x_0)) P(x0,f(x0)) 处的切线的斜率。
偏导数
偏导数描述了多变量函数沿着某一坐标轴方向的变化率,此时将其他变量视为常数。
-
数学定义: \textbf{数学定义:} 数学定义: 对于 n n n 元函数 f ( x 1 , x 2 , . . . , x n ) f(x_1, x_2, ..., x_n) f(x1,x2,...,xn),其在点 P 0 ( a 1 , a 2 , . . . , a n ) P_0(a_1, a_2, ..., a_n) P0(a1,a2,...,an) 处对变量 x i x_i xi 的偏导数为:
∂ f ( P 0 ) ∂ x i = lim ( h → 0 ) f ( a 1 , … , a i + h , . . . , a n ) − f ( a 1 , . . . , a i , . . . , a n ) h \frac{\partial f(P_0)}{\partial x_i} = \lim_{(h\rightarrow 0)} \frac{f(a_1,\dots, a_i + h, ..., a_n) - f(a_1, ..., a_i, ..., a_n)}{h} ∂xi∂f(P0)=(h→0)limhf(a1,…,ai+h,...,an)−f(a1,...,ai,...,an) -
几何意义: \textbf{几何意义:} 几何意义: 函数 z = f ( x , y ) z = f(x, y) z=f(x,y) 的图像是一个三维空间中的曲面。
偏导数 ∂ f ∂ x \frac{\partial f}{\partial x} ∂x∂f 的几何意义为:用平面 y = y 0 y = y_0 y=y0 去截曲面 S S S,得到一条截面曲线 C 1 C_1 C1。这条曲线位于平面 y = y 0 y = y_0 y=y0 上,其方程可以看作 z = f ( x , y 0 ) z = f(x, y₀) z=f(x,y0) (此时 y 0 y_0 y0是常数, z z z 仅随 x x x 变化)。通俗而言,站在山上的某一点 ( x 0 , y 0 ) (x_0, y_0) (x0,y0),保持该位置 y y y坐标不变,只沿着 x x x坐标走。脚下这条路径(截面曲线 C 1 C_1 C1)在当前点的坡度就是函数 f f f对 x x x 方向的偏导数
方向导数
方向导数描述了函数在某一点沿特定方向的瞬时变化率,其数学定义为:
\qquad
设
f
f
f 是一个定义在
R
n
\R^n
Rn中的多元函数,
P
0
P_0
P0是定义域内的一点,
u
u
u为一个单位方向向量,则函数
f
f
f 在点
P
0
P_0
P0 沿方向
u
u
u 的方向导数
D
u
f
(
P
0
)
D_u f(P_0)
Duf(P0)定义为:
D
u
f
(
P
0
)
=
lim
(
h
→
0
)
f
(
P
0
+
h
∗
u
)
−
f
(
P
0
)
h
D_u f(P_0) = \lim_{(h \rightarrow 0)}\frac{f(P_0 + h*u) - f(P_0)}{h}
Duf(P0)=(h→0)limhf(P0+h∗u)−f(P0)
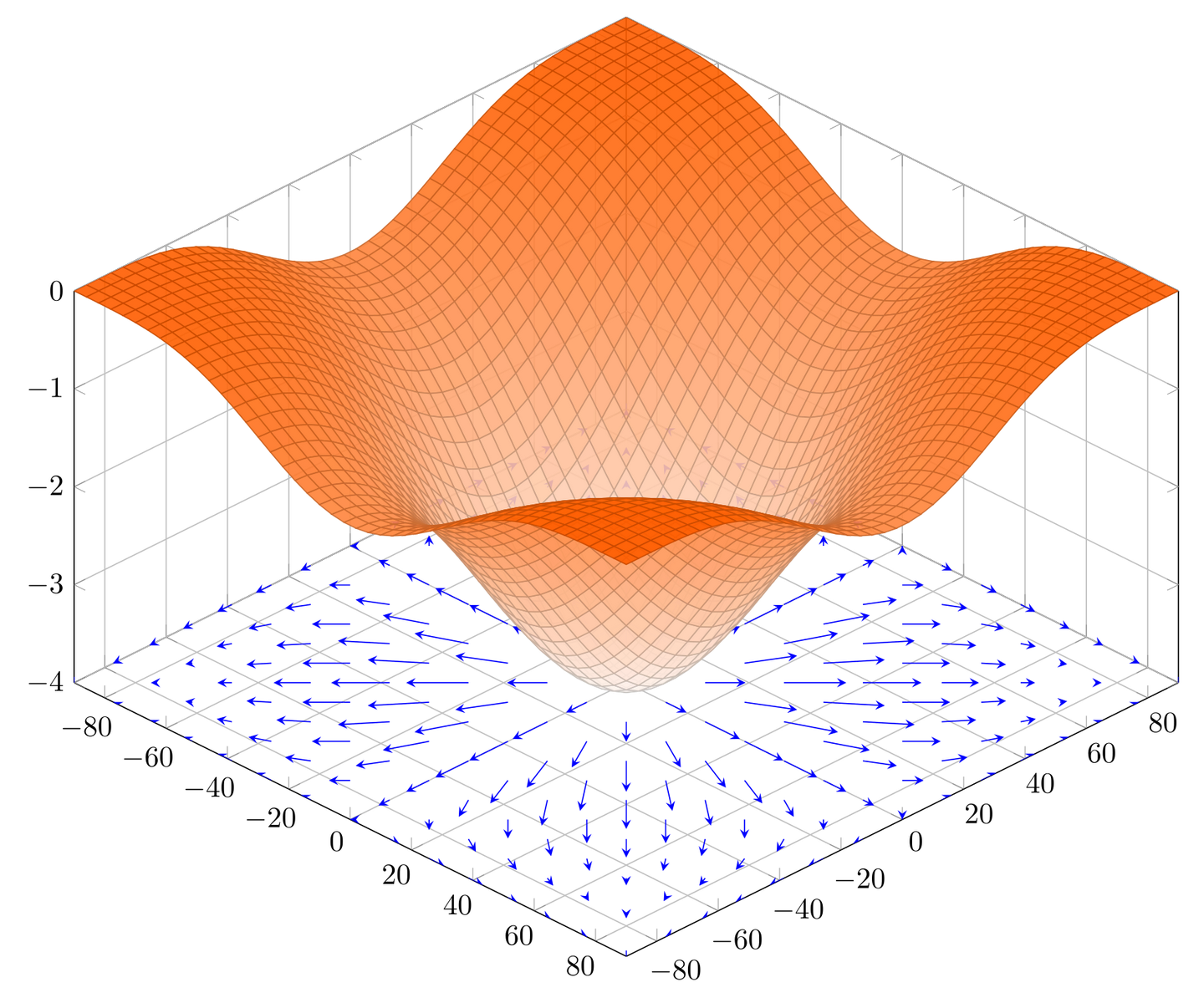
图片引用自: https://pic4.zhimg.com/v2-f815c6d5a4294a05fc23a407b7550d11_1440w.jpg
梯度
-
数学定义: \textbf{数学定义:} 数学定义: 对于 n n n维空间 R n \R^n Rn 中的函数 f ( x ) f(\textbf{x}) f(x),其中 x = ( x 1 , x 2 , … , x n ) T \textbf{x} = (x_1, x_2, \dots, x_n)^T x=(x1,x2,…,xn)T ,如果 f f f 在点 x x x 的所有偏导数都存在,则 f f f在点 x x x 的梯度 ∇ f ( x ) \nabla f(\textbf{x}) ∇f(x)或 g r a d f ( x ) grad f(\textbf{x}) gradf(x)定义为:
∇ f ( x ) = ( ∂ f / ∂ x 1 , ∂ f / ∂ x 2 , … , ∂ f / ∂ x n ) T \nabla f(\textbf{x}) = (\partial f/\partial x_1, \partial f/\partial x_2, \dots, \partial f/\partial x_n)^T ∇f(x)=(∂f/∂x1,∂f/∂x2,…,∂f/∂xn)T
其中, ∂ f / ∂ x i \partial f/\partial x_i ∂f/∂xi表示函数 f f f 关于变量 x i x_i xi 的偏导数。 -
几何意义: \textbf{几何意义:} 几何意义: 在函数定义域内的某一点 x x x,梯度向量 ∇ f ( x ) \nabla f(\textbf{x}) ∇f(x) 指向该点函数值增长最快的方向。梯度向量的模 ∣ ∣ ∇ f ( x ) ∣ ∣ ||\nabla f(x)|| ∣∣∇f(x)∣∣ 表示在这个最快增长方向上的增长率,其计算为:
∣ ∣ ∇ f ( x ) ∣ ∣ = ( ∂ f / ∂ x 1 ) 2 , ( ∂ f / ∂ x 2 ) 2 , … , ( ∂ f / ∂ x n ) 2 ||\nabla f(x)|| = \sqrt{(\partial f/\partial x_1)^2, (\partial f/\partial x_2)^2, \dots, (\partial f/\partial x_n)^2} ∣∣∇f(x)∣∣=(∂f/∂x1)2,(∂f/∂x2)2,…,(∂f/∂xn)2 -
与方向导数的关系: \textbf{与方向导数的关系:} 与方向导数的关系: 函数 f f f在点 x x x 沿方向 u u u 的方向导数 D u f ( x ) D_u f(x) Duf(x) 可以通过梯度计算:
D u f ( x ) = ∇ f ( x ) ⋅ u = ∣ ∣ ∇ f ( x ) ∣ ∣ ⋅ ∣ ∣ u ∣ ∣ ⋅ cos ( θ ) = ∣ ∣ ∇ f ( x ) ∣ ∣ ⋅ cos ( θ ) D_u f(x) = \nabla f(x) \cdot u = ||\nabla f(x)||\cdot||u||\cdot \cos(θ) = ||\nabla f(x)||\cdot \cos(\theta) Duf(x)=∇f(x)⋅u=∣∣∇f(x)∣∣⋅∣∣u∣∣⋅cos(θ)=∣∣∇f(x)∣∣⋅cos(θ)
其中, θ \theta θ是梯度向量 ∇ f ( x ) \nabla f(x) ∇f(x)与方向向量 u u u 之间的夹角。- 当 u u u 与 ∇ f ( x ) \nabla f(x) ∇f(x) 方向相同时 ( θ = 0 , cos ( θ ) = 1 \theta = 0, \cos(\theta) = 1 θ=0,cos(θ)=1),方向导数取得最大值 ∣ ∣ ∇ f ( x ) ∣ ∣ ||\nabla f(x)|| ∣∣∇f(x)∣∣.
- 当 u u u 与 ∇ f ( x ) \nabla f(x) ∇f(x) 方向相反时 ( θ = π , cos ( θ ) = − 1 \theta = \pi, \cos(\theta) = -1 θ=π,cos(θ)=−1),方向导数取得最小值 − ∣ ∣ ∇ f ( x ) ∣ ∣ -||\nabla f(x)|| −∣∣∇f(x)∣∣,这表明 − ∇ f ( x ) -\nabla f(x) −∇f(x) 指向函数值减小最快的方向.
- 当 u u u 与 ∇ f ( x ) \nabla f(x) ∇f(x) 正交时 ( θ = π 2 , cos ( θ ) = 0 \theta = \frac{\pi}{2}, \cos(\theta) = 0 θ=2π,cos(θ)=0),方向导数为 0 0 0,表示在该方向函数值瞬时不变.
- 总结:梯度是一个方向向量,定义了函数上升最快的方向,在这个方向上函数有最大的变化率,其数值等于梯度的模.
Hessian矩阵
海森矩阵是一个方阵,由一个多元函数的二阶偏导数组成。它描述了函数的局部曲率。
\qquad
假设一个
n
n
n 元实值函数
f
(
x
)
f(\textbf{x})
f(x),其中
x
=
(
x
1
,
x
2
,
.
.
.
,
x
n
)
T
\textbf{x} = (x_1, x_2, ..., x_n)^T
x=(x1,x2,...,xn)T 是一个
n
n
n 维向量。如果函数
f
f
f 的所有二阶偏导数都存在且连续,则其Hessian矩阵
H
(
x
)
H(\textbf{x})
H(x) 或
∇
2
f
(
x
)
\nabla^2 f(\textbf{x})
∇2f(x) 定义为一个
n
×
n
n × n
n×n 的对称矩阵:
H
(
x
)
=
(
∂
2
f
∂
x
1
2
∂
2
f
∂
x
1
∂
x
2
⋯
∂
2
f
∂
x
1
∂
x
n
∂
2
f
∂
x
2
∂
x
1
∂
2
f
∂
x
2
2
⋯
∂
2
f
∂
x
2
∂
x
n
⋮
⋮
⋮
⋮
∂
2
f
∂
x
n
∂
x
1
∂
2
f
∂
x
n
∂
x
2
⋯
∂
2
f
∂
x
n
2
)
\begin{align*} H(\textbf{x})= \begin{pmatrix} \frac{\partial^2 f}{\partial x_1^2} & \frac{\partial^2 f}{\partial x_1 \partial x_2} & \cdots & \frac{\partial^2 f}{\partial x_1 \partial x_n} \\ \\ \frac{\partial^2 f}{\partial x_2 \partial x_1} & \frac{\partial^2 f}{\partial x_2^2} & \cdots & \frac{\partial^2 f}{\partial x_2 \partial x_n} \\ \vdots & \vdots & \vdots & \vdots \\ \frac{\partial^2 f}{\partial x_n \partial x_1} & \frac{\partial^2 f}{\partial x_n \partial x_2} & \cdots & \frac{\partial^2 f}{\partial x_n^2} \\ \end{pmatrix} \end{align*}
H(x)=
∂x12∂2f∂x2∂x1∂2f⋮∂xn∂x1∂2f∂x1∂x2∂2f∂x22∂2f⋮∂xn∂x2∂2f⋯⋯⋮⋯∂x1∂xn∂2f∂x2∂xn∂2f⋮∂xn2∂2f
其中,矩阵的第
(
i
,
j
)
(i, j)
(i,j) 个元素是
∂
2
f
∂
x
i
∂
x
j
\frac{\partial^2 f}{\partial x_i \partial x_j}
∂xi∂xj∂2f.
Hessian矩阵的几何意义
Hessian矩阵在某一点的值,描述了该点附近函数图像的局部曲率或弯曲程度。
-
与二次型的联系: \textbf{与二次型的联系:} 与二次型的联系:
多变量函数的二阶泰勒展开式在某点 x 0 x_0 x0附近可以近似表示为:
f ( x ) ≈ f ( x 0 ) + ∇ f ( x 0 ) T ( x − x 0 ) + 1 2 ( x − x 0 ) T H ( x 0 ) ( x − x 0 ) f(x) \approx f(x_0) + \nabla f(x_0)^T(x - x_0) + \frac{1}{2}(x - x_0)^T H(x_0) (x - x_0) f(x)≈f(x0)+∇f(x0)T(x−x0)+21(x−x0)TH(x0)(x−x0)
其中: ∇ f ( x 0 ) \nabla f(x_0) ∇f(x0)是梯度向量,表示函数在 x 0 x_0 x0 处的线性变化率。 H ( x 0 ) H(x_0) H(x0)是Hessian矩阵在 x 0 x_0 x0处的值。 ( x − x 0 ) T H ( x 0 ) ( x − x 0 ) (x - x_0)^T H(x_0) (x - x_0) (x−x0)TH(x0)(x−x0) 是一个二次型,它决定了函数在梯度为零的点(临界点)附近的形状。 -
Hessian矩阵的特征值与曲率方向: \textbf{Hessian矩阵的特征值与曲率方向:} Hessian矩阵的特征值与曲率方向:
Hessian矩阵是实对称矩阵,其特征值都是实数,并且存在一组正交的特征向量。特征向量指示了函数在 x 0 x_0 x0点附近主要的弯曲方向(主曲率方向);特征值对应于这些主曲率方向上的曲率大小。- 正特征值:表示在该特征向量方向上,函数图像是向上弯曲的。特征值越大,弯曲越剧烈。
- 负特征值: 表示在该特征向量方向上,函数图像是向下弯曲的。特征值的绝对值越大,弯曲越剧烈。
- 零特征值: 表示在该特征向量方向上,函数图像可能是平坦的,或者弯曲情况更复杂,需要更高阶导数来判断。
-
Hessian矩阵的正定性/负定性与函数形状: \textbf{Hessian矩阵的正定性/负定性与函数形状:} Hessian矩阵的正定性/负定性与函数形状:
Hessian矩阵在某点 x 0 x_0 x0的性质(正定、负定等)直接关系到该点附近函数的局部形状,其中,必要的前提是 ∇ f ( x 0 ) = 0 \nabla f(x_0) = 0 ∇f(x0)=0,意味着函数在该点的所有方向上的导数均为 0 0 0,即该点是一个临界点:- H ( x 0 ) H(x_0) H(x0)是正定矩阵: 所有特征值都为正。这意味着在 x 0 x_0 x0的所有方向上,函数都是向上弯曲的。如果 ∇ f ( x 0 ) = 0 \nabla f(x_0) = 0 ∇f(x0)=0,则 x 0 x_0 x0是一个严格局部极小点。函数图像在 x 0 x_0 x0附近像一个朝上的碗口。
- H ( x 0 ) H(x_0) H(x0)是负定矩阵: 所有特征值都为负。这意味着在 x 0 x_0 x0的所有方向上,函数都是向下弯曲的。如果 ∇ f ( x 0 ) = 0 \nabla f(x_0) = 0 ∇f(x0)=0,则 x 0 x_0 x0是一个严格局部极大点。函数图像在 x 0 x_0 x0附近像一个倒扣的碗口(或山峰)。
- H ( x 0 ) H(x_0) H(x0)是不定矩阵: 特征值中既有正的也有负的。这意味着在某些方向上函数向上弯曲,在另一些方向上函数向下弯曲。如果 ∇ f ( x 0 ) = 0 \nabla f(x_0) = 0 ∇f(x0)=0,则 x 0 x_0 x0是一个鞍点。函数图像在 x 0 x_0 x0附近像一个马鞍。
- H ( x 0 ) H(x_0) H(x0)是半正定矩阵: 所有特征值非负,且至少有一个为零。如果 ∇ f ( x 0 ) = 0 \nabla f(x_0) = 0 ∇f(x0)=0, x 0 x_0 x0可能是局部极小点,也可能不是(例如 f ( x ) = x 3 f(x) = x^3 f(x)=x3在 x = 0 x=0 x=0)。函数图像在某些方向上可能是平坦的。
- H ( x 0 ) H(x_0) H(x0)是半负定矩阵: 所有特征值非正,且至少有一个为零。如果 ∇ f ( x 0 ) = 0 \nabla f(x_0) = 0 ∇f(x0)=0, x 0 x_0 x0可能是局部极大点,也可能不是。
泰勒展开
泰勒展开的定义与核心思想
泰勒展开的核心思想是用一个多项式函数来逼近一个在某点附近具有足够阶数导数的函数。 这个多项式的系数由函数在该点的各阶导数值决定。
如果一个函数
f
(
x
)
f(x)
f(x)在点
x
0
x_0
x0处具有
n
n
n阶导数,那么
f
(
x
)
f(x)
f(x)在
x
0
x_0
x0点的
n
n
n阶泰勒展开式为:
P
n
(
x
)
=
f
(
x
0
)
+
f
′
(
x
0
)
(
x
−
x
0
)
+
f
′
′
(
x
0
)
2
!
(
x
−
x
0
)
2
+
⋯
+
f
n
(
x
0
)
n
!
)
(
x
−
x
0
)
n
P_n(x) = f(x_0) + f^{'}(x_0)(x - x_0) + \frac{f^{''}(x_0)}{2!}(x - x_0)^2 + \cdots + \frac{f^n(x_0)}{n!})(x - x_0)^n
Pn(x)=f(x0)+f′(x0)(x−x0)+2!f′′(x0)(x−x0)2+⋯+n!fn(x0))(x−x0)n
可以更紧凑地写作:
P
n
(
x
)
=
∑
k
=
0
n
f
k
(
x
0
)
k
!
(
x
−
x
0
)
k
P_n(x) = \sum_{k=0}^{n} \frac{f^k(x₀)}{k!}(x - x₀)^k
Pn(x)=k=0∑nk!fk(x0)(x−x0)k
其中:
f
k
(
x
0
)
f^k(x_0)
fk(x0) 表示函数
f
f
f在点
x
0
x_0
x0处的
k
k
k阶导数且
f
0
(
x
0
)
=
f
(
x
0
)
f^0(x₀) = f(x₀)
f0(x0)=f(x0)。当泰勒展开的点
x
0
=
0
x_0 = 0
x0=0 时,得到的特殊形式称为麦克劳林展开:
P
n
(
x
)
=
f
(
0
)
+
f
′
(
0
)
x
+
f
′
′
(
0
)
2
!
x
2
+
⋯
+
f
n
(
0
)
n
!
x
n
P_n(x) = f(0) + f^{'}(0)x + \frac{f^{''}(0)}{2!}x² + \cdots + \frac{f^n(0)}{n!}x^n
Pn(x)=f(0)+f′(0)x+2!f′′(0)x2+⋯+n!fn(0)xn
泰勒定理与余项
泰勒多项式
P
n
(
x
)
P_n(x)
Pn(x)是对
f
(
x
)
f(x)
f(x)的一个近似。泰勒定理精确地描述了这个近似的误差,该误差被称为余项或截断误差,记作
R
n
(
x
)
R_n(x)
Rn(x),则基于泰勒定理的函数
f
(
x
)
f(x)
f(x)的表达式为:
f
(
x
)
=
P
n
(
x
)
+
R
n
(
x
)
f(x) = P_n(x) + R_n(x)
f(x)=Pn(x)+Rn(x)即
f
(
x
)
=
∑
k
=
0
n
f
k
(
x
0
)
k
!
(
x
−
x
0
)
k
+
R
n
(
x
)
f(x) = \sum_{k=0}^{n} \frac{f^k(x₀)}{k!}(x - x₀)^k + R_n(x)
f(x)=k=0∑nk!fk(x0)(x−x0)k+Rn(x) 余项
R
n
(
x
)
R_n(x)
Rn(x)最常见的两种表达形式为是:
- 拉格朗日余项:
如果 f f f在包含 x 0 x_0 x0和 x x x的闭区间上 n + 1 n+1 n+1阶可导,则余项可以表示为:
R n ( x ) = f n + 1 ( ξ ) ( n + 1 ) ! ( x − x 0 ) n + 1 R_n(x) = \frac{f^{n+1}(\xi)}{(n+1)!}(x - x_0)^{n+1} Rn(x)=(n+1)!fn+1(ξ)(x−x0)n+1 其中 ξ \xi ξ是一个介于 x 0 x_0 x0和 x x x之间的某个数。这个形式的余项表明,误差与 ( x − x 0 ) n + 1 (x - x_0)^{n+1} (x−x0)n+1和函数在某未知点的 n + 1 n+1 n+1阶导数有关。 - 佩亚诺余项:
如果 f f f在 x 0 x_0 x0处 n n n阶可导,则余项可以表示为:
R n ( x ) = o ( ( x − x 0 ) n ) R_n(x) = o((x - x₀)^n) Rn(x)=o((x−x0)n) 这意味着
lim ( x → x 0 ) R n ( x ) ( x − x 0 ) n = 0 \lim_{(x\rightarrow x_0)}\frac{R_n(x)}{(x - x₀)^n}= 0 (x→x0)lim(x−x0)nRn(x)=0
皮亚诺余项表明,当 x x x趋近于 x 0 x_0 x0时,余项是比 ( x − x 0 ) n (x - x_0)^n (x−x0)n更高阶的无穷小量。它描述了误差的阶次,但不给出具体的误差界。
如果函数
f
(
x
)
f(x)
f(x)在
x
0
x_0
x0处无穷阶可导,并且当
n
→
∞
n \rightarrow \infty
n→∞时,余项
R
n
(
x
)
→
0
R_n(x) \rightarrow 0
Rn(x)→0,则泰勒展开式可以写成无穷级数,称为
f
(
x
)
f(x)
f(x)在
x
0
x_0
x0点的泰勒级数:
f
(
x
)
=
∑
k
=
0
∞
f
k
(
x
0
)
k
!
(
x
−
x
0
)
k
f(x) =\sum_{k=0}^{\infty} \frac{f^k(x_0)}{k!}(x - x_0)^k
f(x)=k=0∑∞k!fk(x0)(x−x0)k 在这种情况下,泰勒级数精确地等于原函数
f
(
x
)
f(x)
f(x)。
泰勒展开的几何意义
泰勒展开的几何意义在于,用一系列越来越精确的多项式函数来局部地逼近原函数的图像。泰勒多项式 P n ( x ) P_n(x) Pn(x)在 x 0 x_0 x0点与原函数 f ( x ) f(x) f(x)具有相同的前 n n n阶导数值。
-
零阶泰勒展开 ( n = 0 ) (n=0) (n=0):
P 0 ( x ) = f ( x 0 ) P_0(x) = f(x_0) P0(x)=f(x0)
几何意义: 用一个常数函数(一条水平线)来近似 f ( x ) f(x) f(x)在 x 0 x_0 x0附近的值。这条水平线通过点 ( x 0 , f ( x 0 ) ) (x_0, f(x_0)) (x0,f(x0)),这是最粗糙的近似。 -
一阶泰勒展开 ( n = 1 ) (n=1) (n=1):
P 1 ( x ) = f ( x 0 ) + f ′ ( x 0 ) ( x − x 0 ) P_1(x) = f(x_0) + f^{'}(x_0)(x - x_0) P1(x)=f(x0)+f′(x0)(x−x0)
几何意义: 用一条直线来近似 f ( x ) f(x) f(x)在 x 0 x_0 x0附近的图像。这条直线就是函数 f ( x ) f(x) f(x)在点 ( x 0 , f ( x 0 ) ) (x_0, f(x_0)) (x0,f(x0))处的切线,这个线性近似捕捉了函数在 x 0 x_0 x0点的局部线性和变化趋势(由导数 f ′ ( x 0 ) f^{'}(x₀) f′(x0)决定斜率)。 -
二阶泰勒展开 ( n = 2 ) (n=2) (n=2):
P 2 ( x ) = f ( x 0 ) + f ′ ( x 0 ) ( x − x 0 ) + f ′ ′ ( x 0 ) 2 ! ( x − x 0 ) 2 P_2(x) = f(x_0) + f^{'}(x_0)(x - x_0) + \frac{f^{''}(x_0)}{2!}(x - x_0)^2 P2(x)=f(x0)+f′(x0)(x−x0)+2!f′′(x0)(x−x0)2
几何意义: 用一个二次函数(一条抛物线)来近似 f ( x ) f(x) f(x)在 x 0 x_0 x0附近的图像。这个抛物线不仅在 x 0 x_0 x0点与原函数有相同的函数值和一阶导数值,而且还具有相同的二阶导数值。这个二次近似比线性近似能更好地捕捉函数的局部弯曲特性。
二阶导数 f ′ ′ ( x 0 ) f^{''}(x_0) f′′(x0)描述了函数图像在 x 0 x_0 x0点的曲率或弯曲程度。- 如果 f ′ ′ ( x 0 ) > 0 f^{''}(x_0)>0 f′′(x0)>0,抛物线开口向上,表示函数在该点局部是向上弯曲的(凸的)。
- 如果 f ′ ′ ( x 0 ) < 0 f^{''}(x_0)<0 f′′(x0)<0,抛物线开口向下,表示函数在该点局部是向下弯曲的(凹的)。
- 如果 f ′ ′ ( x 0 ) = 0 f^{''}(x_0)=0 f′′(x0)=0,抛物线退化为直线(如果 f ′ ( x 0 ) f^{'}(x_0) f′(x0)非零)或水平线(如果 f ′ ( x 0 ) f^{'}(x_0) f′(x0)也为零),弯曲情况不明显,可能需要更高阶项。
-
高阶泰勒展开 ( n > 2 ) (n > 2) (n>2):
随着阶数 n n n的增加,泰勒多项式 P n ( x ) P_n(x) Pn(x)会使用更高阶的导数信息,从而在 x 0 x_0 x0点附近能够更精确地拟合原函数 f ( x ) f(x) f(x)的形状,捕捉更细微的弯曲和变化特征。 -
总结:
- 常数项 f ( x 0 ) f(x_0) f(x0): 定位了函数在 x 0 x_0 x0点的高度。
- 一次项 f ′ ( x 0 ) ( x − x 0 ) f^{'}(x_0)(x - x_0) f′(x0)(x−x0): 描述了函数在 x 0 x_0 x0点的局部线性趋势(切线)。
- 二次项 f ′ ′ ( x 0 ) 2 ! ( x − x 0 ) 2 \frac{f^{''}(x_0)}{2!}(x - x_0)^2 2!f′′(x0)(x−x0)2: 描述了函数在 x 0 x_0 x0点的局部弯曲程度(曲率)。
- 更高次项: 描述了更细致的局部形状特征。
多变量函数的泰勒展开
泰勒展开的思想推广到多变量函数。对于一个
n
n
n元函数
f
(
x
)
f(\textbf{x})
f(x),其中
x
=
(
x
1
,
⋯
,
x
n
)
T
\textbf{x} = (x_1, \cdots, x_n)^T
x=(x1,⋯,xn)T,在点
x
0
\textbf{x}_0
x0附近的泰勒展开式(以二阶为例):
f
(
x
)
≈
f
(
x
0
)
+
∇
f
(
x
0
)
T
(
x
−
x
0
)
+
1
2
(
x
−
x
0
)
T
H
(
x
0
)
(
x
−
x
0
)
f(\textbf{x}) \approx f(\textbf{x}_0) + \nabla f(\textbf{x}_0)^T(\textbf{x} - \textbf{x}_0) + \frac{1}{2}(\textbf{x} - \textbf{x}_0)^T H(\textbf{x}_0) (\textbf{x} - \textbf{x}_0)
f(x)≈f(x0)+∇f(x0)T(x−x0)+21(x−x0)TH(x0)(x−x0)
其中:
∇
f
(
x
0
)
\nabla f(\textbf{x}_0)
∇f(x0)是函数
f
f
f在
x
0
\textbf{x}_0
x0点的梯度向量,是一个列向量,包含了所有一阶偏导数:
∇
f
(
x
0
)
=
[
∂
f
(
x
0
)
∂
x
1
,
∂
f
(
x
0
)
∂
x
2
,
⋯
,
∂
f
(
x
0
)
∂
x
n
]
T
\nabla f(\textbf{x}_0) = [\frac{\partial f(\textbf{x}_0)}{\partial x_1},\frac{\partial f(\textbf{x}_0)}{\partial x_2},\cdots , \frac{\partial f(\textbf{x}_0)}{\partial x_n}]^T
∇f(x0)=[∂x1∂f(x0),∂x2∂f(x0),⋯,∂xn∂f(x0)]T
H
(
x
0
)
H(x_0)
H(x0)是函数
f
f
f在
x
0
x_0
x0点的Hessian矩阵,包含了所有二阶偏导数,
(
x
−
x
0
)
(x - x_0)
(x−x0)是位移向量。
几何意义: \textbf{几何意义:} 几何意义:
- 零阶展开 f ( x 0 ) : f(x_0): f(x0): 函数在 x 0 x_0 x0点的值。
- 一阶展开
f
(
x
0
)
+
∇
f
(
x
0
)
T
(
x
−
x
0
)
:
f(x_0) + \nabla f(x_0)^T(x - x_0):
f(x0)+∇f(x0)T(x−x0):
- 一个线性函数,其图像是一个切超平面,它在点 ( x 0 , f ( x 0 ) ) (x_0, f(x_0)) (x0,f(x0))处与函数 f ( x ) f(x) f(x)的曲面相切。
- 梯度 ∇ f ( x 0 ) \nabla f(x_0) ∇f(x0)指向函数 f ( x ) f(x) f(x)在 x 0 x_0 x0点增长最快的方向,其大小表示增长的速率。
- 二阶展开
f
(
x
0
)
+
∇
f
(
x
0
)
T
(
x
−
x
0
)
+
1
2
(
x
−
x
0
)
T
H
(
x
0
)
(
x
−
x
0
)
:
f(x_0) + \nabla f(x_0)^T(x - x_0) + \frac{1}{2}(x - x_0)^T H(x_0) (x - x_0):
f(x0)+∇f(x0)T(x−x0)+21(x−x0)TH(x0)(x−x0):
- 一个二次函数,其图像是一个二次曲面 (例如椭球面、抛物面、双曲面等),其在 x 0 x_0 x0点附近更好地逼近原函数的曲面。
- Hessian矩阵
H
(
x
0
)
H(x_0)
H(x0)描述了函数曲面在
x
0
x_0
x0点的局部曲率。
H
(
x
0
)
H(x_0)
H(x0)的特征值和特征向量决定了曲面的主曲率方向和大小。
- H ( x 0 ) H(x_0) H(x0)正定,曲面在 x 0 x_0 x0附近局部向上凸
- H ( x 0 ) H(x_0) H(x0)负定,曲面在 x 0 x_0 x0附近局部向下凹
- H ( x 0 ) H(x_0) H(x0)不定,曲面在 x 0 x_0 x0附近呈鞍形
最优化问题的基本概念
最优化问题数学模型
目标函数: min f ( x ) 约束条件:s.t. x ∈ Ω ( 可行域 ) : = { g i ( x ) ≤ 0 , i = 1 , 2 , … , p (不等式约束) h j ( x ) = 0 , j = 1 , 2 , … , q (等式约束) \begin{align*} &目标函数:\min f(x) \\ &约束条件:\text{s.t.} x \in \Omega(可行域) := \begin{cases} g_i(x) \le 0,i=1,2,\dots,p \quad (不等式约束)\\ h_j(x)=0,j=1,2,\dots,q \quad (等式约束) \end{cases} \end{align*} 目标函数:minf(x)约束条件:s.t.x∈Ω(可行域):={gi(x)≤0,i=1,2,…,p(不等式约束)hj(x)=0,j=1,2,…,q(等式约束)
最优化问题的最优解
对于最小化问题,最优解 x ∗ x^* x∗分别定义为:
- 局部最优解:在可行域内的一个点 x ∗ x^* x∗ ,使得在其某个邻域内的所有可行点 x ∗ + δ x^*+ \delta x∗+δ,都有 f ( x ∗ ) ≤ f ( x ∗ + δ ) f(x^*) ≤ f(x^*+\delta) f(x∗)≤f(x∗+δ) 。
- 全局最优解: 在整个可行域内的一个点 x ∗ x^* x∗ ,使得对于所有可行点 x x x,都有 f ( x ∗ ) ≤ f ( x ) f(x^*) \le f(x) f(x∗)≤f(x).
- 严格局部/全局最优解: 上述不等式为严格不等式 (<)。
凸优化
凸集
定义:
\textbf{定义:}
定义: 集合
C
⊆
R
n
C \subseteq R^n
C⊆Rn被称为凸集,如果对于集合
C
C
C中的任意两点
x
1
,
x
2
x_1, x_2
x1,x2,连接这两点的线段上的所有点也都属于集合
C
C
C。其数学表达为:对于任意
x
1
,
x
2
∈
C
x_1, x_2 \in C
x1,x2∈C 和任意
θ
∈
[
0
,
1
]
\theta \in [0, 1]
θ∈[0,1],都有
θ
x
1
+
(
1
−
θ
)
x
2
∈
C
\theta x_1 + (1 - \theta)x_2 \in C
θx1+(1−θ)x2∈C 表达式
θ
x
1
+
(
1
−
θ
)
x
2
\theta x_1 + (1 - \theta)x_2
θx1+(1−θ)x2被称为
x
1
x_1
x1和
x
2
x_2
x2的凸组合。
凸组合
定义:
\textbf{定义:}
定义: 给定
R
n
R^n
Rn空间中的
k
k
k个点
x
1
,
x
2
,
⋯
,
x
k
x_1, x_2, \cdots, x_k
x1,x2,⋯,xk,这些点的一个凸组合是一个新的点
x
x
x,其数学表达形式为:
x
=
θ
1
x
1
,
θ
2
x
2
,
⋯
,
θ
k
x
k
x = \theta_1 x_1, \theta_2 x_2, \cdots, \theta_k x_k
x=θ1x1,θ2x2,⋯,θkxk 其中
- 非负性: θ i ≥ 0 θ_i \ge 0 θi≥0 ; ∀ i = 1 , 2 , ⋯ , k \forall i = 1, 2, \cdots, k ∀i=1,2,⋯,k
- 和为一: ∑ i = 1 k θ i = 1 \sum_{i=1}^{k}{\theta_i}=1 ∑i=1kθi=1
凸函数
定义:
\textbf{定义:}
定义: 一个定义在凸集
C
C
C上的函数
f
:
C
→
R
f: C \rightarrow R
f:C→R被称为凸函数,如果对于任意
x
1
,
x
2
∈
C
x_1, x_2 \in C
x1,x2∈C 和任意
α
∈
[
0
,
1
]
\alpha \in [0, 1]
α∈[0,1],都有
f
(
α
x
1
+
(
1
−
α
)
x
2
)
≤
α
f
(
x
1
)
+
(
1
−
α
)
f
(
x
2
)
f(\alpha x_1 + (1 - \alpha)x_2) \le \alpha f(x_1) + (1 - \alpha)f(x_2)
f(αx1+(1−α)x2)≤αf(x1)+(1−α)f(x2) 直观上,函数图像上任意两点之间的弦都在这两点之间的函数图像的上方。
- 严格凸函数: 不等式严格成立 (即 <)
- 凹函数: 如果 -f 是凸函数,则 f 是凹函数。不等式方向相反 f ( α x 1 + ( 1 − α ) x 2 ) ≥ α f ( x 1 ) + ( 1 − α ) f ( x 2 ) f(\alpha x_1 + (1 - \alpha)x_2) \ge \alpha f(x_1) + (1 - \alpha)f(x_2) f(αx1+(1−α)x2)≥αf(x1)+(1−α)f(x2)。
凹/凸函数的实例:
\textbf{凹/凸函数的实例:}
凹/凸函数的实例:
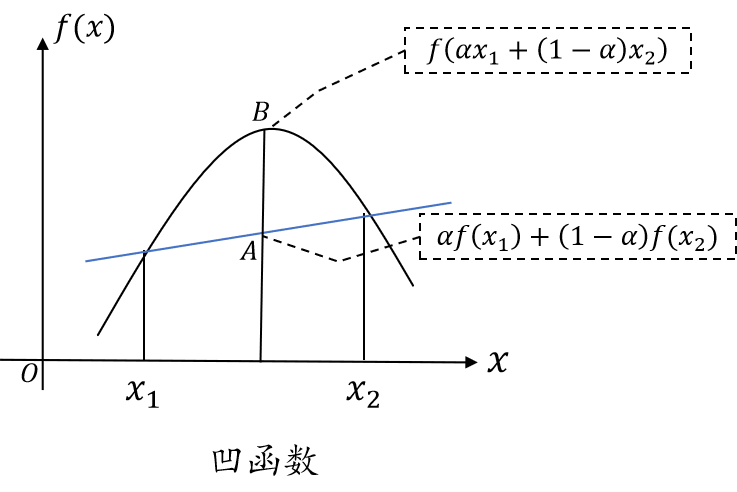
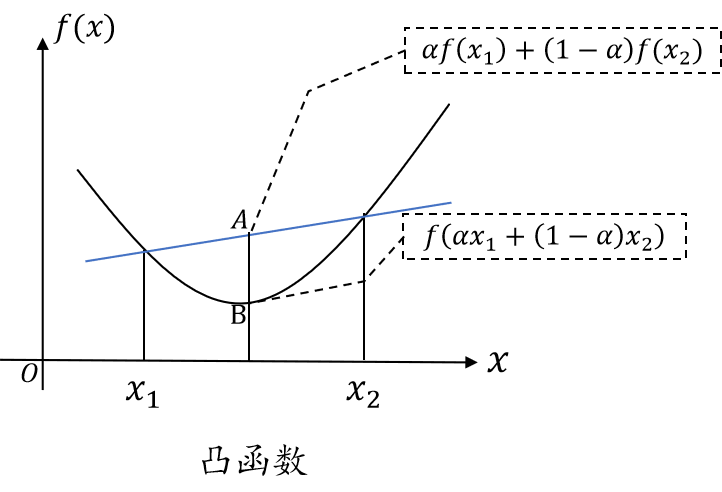
凸性的判断:
\textbf{凸性的判断:}
凸性的判断:
- 一阶条件: 如果 f f f 可微,则 f f f 是凸函数的充要条件是其定义域是凸集,且对于任意 x , y ∈ d o m ( f ) x, y \in dom(f) x,y∈dom(f),有 f ( y ) ≥ f ( x ) + ∇ f ( x ) T ( y − x ) f(y) \ge f(x) + \nabla f(x)^T(y - x) f(y)≥f(x)+∇f(x)T(y−x)。
- 二阶条件: 如果 f f f 二次可微,则 f f f 是凸函数的充要条件是其定义域是凸集,且其 Hessian 矩阵 ∇ 2 f ( x ) \nabla^2 f(x) ∇2f(x) 在定义域内处处半正定 ( ∇ 2 f ( x ) ⪰ 0 ) (\nabla^2 f(x) \succeq 0) (∇2f(x)⪰0)。
凸优化问题
定义:
\textbf{定义:}
定义: 一个优化问题被称为凸优化问题,如果它的目标函数是凸函数,并且可行域是一个凸集。其标准形式为:
min
f
(
x
)
s
.
t
.
g
i
(
x
)
≤
0
,
i
=
1
,
⋯
,
m
h
j
(
x
)
=
0
,
j
=
1
,
⋯
,
p
\begin{align*} \min \quad &f(\textbf{x}) \\ s.t. \quad &g_i(\textbf{x}) \le 0, i = 1, \cdots, m \\ &h_j(\textbf{x}) = 0, j = 1, \cdots, p \end{align*}
mins.t.f(x)gi(x)≤0,i=1,⋯,mhj(x)=0,j=1,⋯,p
- x ∈ R n \textbf{x} \in R^n x∈Rn 是优化变量
- f ( x ) f(\textbf{x}) f(x) 是凸的目标函数
- g i ( x ) g_i(\textbf{x}) gi(x)是凸的不等式约束函数
- h j ( x ) h_j(\textbf{x}) hj(x)是仿射的等式约束函数,即 h j ( x ) = a j T x − b j h_j(\textbf{x}) = \textbf{a}_j^T \textbf{x} - b_j hj(x)=ajTx−bj
凸优化最显著的特点: 对于凸优化问题,任何局部最优解都是全局最优解。
凸优化方法分类:
\textbf{凸优化方法分类:}
凸优化方法分类:
- 一阶方法: 仅使用梯度信息。
- 梯度下降法及其变种 (SGD, Momentum, Adam等)
- 共轭梯度法
- 二阶方法: 使用 Hessian 矩阵信息。
- 牛顿法
- 拟牛顿法 (如 BFGS, L-BFGS)
- 内点法 (如 LP, QP, SOCP, SDP)
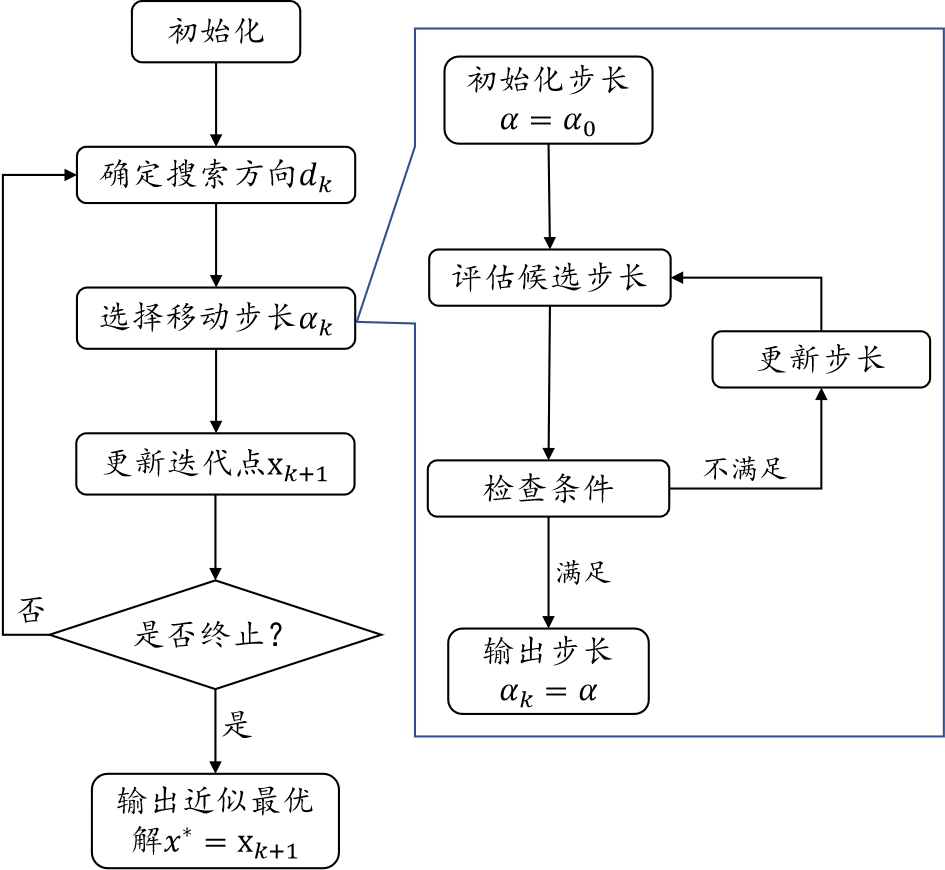
凸优化方法一般算法流程: \textbf{凸优化方法一般算法流程:} 凸优化方法一般算法流程:





















 3837
3837

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








