线性回归推导

        之前看过吴恩达的机器学习入门和神经网络部分，还有李宏毅的深度学习视频，懂了一些知识打了比赛，但是觉得还不够深入，还有好多知识不懂细节不懂推导，还有一些工具没有掌握，加上没有项目经验，现在准备从头开始系统的学习一下。学习的是唐宇迪视频。

        首先一些基本的工具安装和工具的学习只是看着视频跟着敲一敲，准备以后用到，边用边熟悉。

        今天算是第一天，线性回归推导。

1.假设函数提出，hypothesis

        给出样本变量x，通过θ，找出x与y的线性关系，所谓线性代表了在二维中是一条直线（y=θ0+θ1x），在三维中是一个面。通过变换θ尽量的去拟合直线，尽量的使得到的值与原来的值差距小。像下面的这个图（来自ppt）：

得出下面公式，

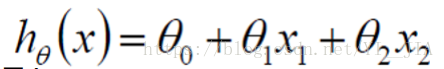
把θ和x看做向量，X0为1，整理得

<