也是看其他大佬的说法。比如这个信息熵是什么? - 知乎
大家都知道 ,对于一个概率分布,信息熵的公式是:
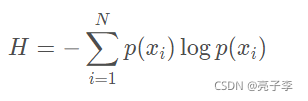
表示
发生的概率。 定义公式我就不再赘述,已经有很多了。确实和我们的印象比较符合,一件事概率越大,他发生了,信息量就越小。太阳天天东边升,一点也不吃惊。太阳哪天从西边来了,说明人类换了东西的叫法。
我们来看一个例子。现在有一条公路,四家公司A,B,C,D负责这条公路的打扫和维护。A来的早,他从里面先选了二分之一。B来了,他占了四分之一,C来了,再选八分之一,D来了,只剩八分之一了。 (请记下下图颜色代表的字母。)

问题在于什么呢?在于我不知道这些公司是负责的哪一段。那现在我想知道,咋办,就需要信息了。 请注意 下面的信息都是二分信息。就是信息只有正反两面。
第一条信息: A在左边 。 一条信息就知道A在哪了 。
第二条信息: B选了右边。 需要 1,2才知道B在哪。
第三条信息:C选了左边。 需要1,2,3知道了C,D。

在上面这条直线上,需要1条信息能够确定的部分是 二分之一。
需要两条信息能够确定的部分是 四分之一
需要三条信息才能够确定的部分是 两个八分之一
就得到了得到总状态需要的信息数:
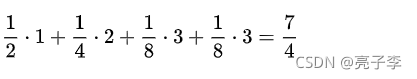
我们再看信息熵的公式。
注意:
在信息熵公式里, log是以2 为底的 ,所以得到了信息熵大小算出来就是 .和确定总状态需要的信息数一模一样。
所以其实我们就知道了。信息熵,就是想要确定整个状态的信息需要的总信息数。
信息熵的单位是比特,可以扩展联想成 需要几个比特位的0/1 。实际上也确实如此,log是以二为底的,所以信息也必须都是二分的信息,只有正反两面,这样算出来才符合结果,这也是为什么A必须左右选一边 而不能选中间的二分之一,因为这时候信息就不是二分的信息了 。
然后来了一个东西叫做KL散度。KL散度的定义是什么,看百科: KL散度是两个几率分布P和Q差别的非对称性的度量。 KL散度是用来度量使用基于Q的分布来编码服从P的分布的样本所需的额外的平均比特数。典型情况下,P表示数据的真实分布,Q表示数据的理论分布、估计的模型分布、或P的近似分布。 看到比特数差这个概念时,我一瞬间就想到了好多。
再来看公式:
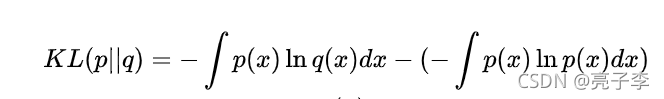
后面我们都知道 Px的信息熵嘛。
前面的 我们怎么理解呢? 首先我们要明确的概念是 P分布的信息熵,就是P分布下编码需要的最小的比特数。 我们看上面的例子会发现,占据最多的A,二分之一,她需要的信息数是最少的。也只有这样, 让占地最多(概率最大)的需要的信息越少,才能得到最小的信息熵。所以用其他的分布来衡量P ,需要的比特数 势必要上升。
比如 现在Q的分布是这样的 ,就是A,B的分布变了。
Q1:
![]()
先代入公式
注意 第一项A这里, log下面是Q中A的概率 是四分之一 但是log上面依然是P中A的概率的倒数,是二分之一的倒数。这就是 用Q分布来表示P分布的样本需要的信息量大小 。是2比特。也就是交叉熵。
用信息的说法呢? 也是一样的。 这里依然是用的P的概率分布,也就是找A要1条信息,B2条,C,D3条。
但是是在Q的分布来衡量的,在Q中B占据了二分之一,也就是需要两条信息的部分变成了二分之一 。 需要一条信息的部分变成了四分之一。
共需要的信息就变成了 :
所以P,Q的交叉熵就是2。
如果Q是下面的分布呢?
Q2:

就是
可以看到 Q2这个图比起上图Q1来说 ,Q的分布和P差的要更远一点。A都变最短了,所以他的交叉熵也要大一点。
上面懂了之后,KL散度就是临门一脚。用交叉熵减去P的信息熵,就是KL散度。含义就是用Q分布来度量P需要的比特数减去P自己度量自己需要的比特数。 对于Q1的例子 KL散度就是2-1.75 = 0.25 对于Q2的例子 KL散度就是2.5-1.75 = 0.75。 所以我们也可以发现KL散度的实际意义,KL散度差的越多,表示Q分布和P分布差的越远。KL散度越小,两个分布就越近。
所以 ,
KL 散度 = Q表示分布需要信息数 - P自己表示分布需要信息数
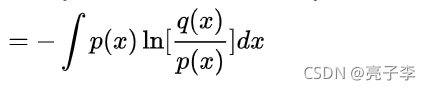





 本文通过实例解析信息熵的概念,将其与实际生活中的公路维护分配相联系,并深入探讨了KL散度,揭示了其作为衡量分布差异的重要工具。重点在于信息熵如何表示所需信息量和KL散度的计算及其在数据编码中的应用。
本文通过实例解析信息熵的概念,将其与实际生活中的公路维护分配相联系,并深入探讨了KL散度,揭示了其作为衡量分布差异的重要工具。重点在于信息熵如何表示所需信息量和KL散度的计算及其在数据编码中的应用。
















 610
610

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








