不同进制之间的转换

• 数的组成

设一个m进制数为abc, 那么该数就是c×m的0次方 加上b×m的1次方 加上a×m的平方。

例如，十进制数123 为 3×10的0次方（即3*1）加2*10的1次方（即2*10），加1*10的平方（即1*100），最后得到123；

二进制数111为1*2的0次方（即1*1）加1*2的1次方（即1*2），加1*2的平方（即1*4），最后得到1+2+4=7；

八进制数25 为5*8的0次方（即5*1）加2*8的1次方（即2*8），最后得到5+16=21；

• 进制转换

其他进制转十进制：理解了上面的例子，把其他任何进制的数转换成十进制都可以用这样的方法，每位上的数字和对应的进制数的几次幂相乘，再把每个结果相加即可。

十进制转二进制：比较简单的方法是把十进制数拆成2的几次幂的结果相加，从最大的开始，例如，十进制数178转换成二进制时，先找到包含的最大的2的整数次幂128（2的7次幂），还剩50,50里面最大的是32（2的5次幂），还剩18,18里面有16和2，分别是4次和1次。现在我们知道第1、4、5、7次幂有数（即该位为1），从右往左写（第一位是0次幂），即为 1011 0010

二进制转八进制： 8是2的3次方，三位二进制数对应一个八进制数，如110 111，可以看成两位八进制数，第一位是110（即6），第二位是111（即7），合起来就是八进制数67。八进制转换成二进制同理，如八进制数71,7和1分别对应三位二进制数111 ， 001， 即111001。

二进制转十六进制：16是2的4次方，四位二进制数对应一个十六进制数，一位十六进制数对应四位二进制数。如二进制数1111 0011，1111对应十六进制F，0011对应16进制3，即十六进制数F3。十六进制转换成二进制同理。如91,9对应1001，1对应0001（不够四位的前面补0，凑成四位），即二进制1001 0001。

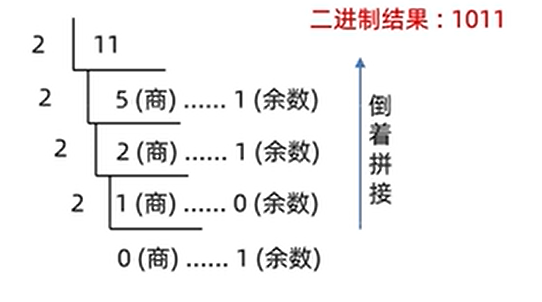
其他进制互换可以先转成十进制再转换成其他进制。下面介绍除基取余法。

要转换成几进制，就除以该进制的基（几进制就是几），例如二进制，就将十进制数一直除以2，直到商为0，将所得余数倒着读。