每日一道leetcode

872. 叶子相似的树 - 力扣（LeetCode）

题目

请考虑一棵二叉树上所有的叶子，这些叶子的值按从左到右的顺序排列形成一个 叶值序列 。

举个例子，如上图所示，给定一棵叶值序列为 (6, 7, 4, 9, 8) 的树。

如果有两棵二叉树的叶值序列是相同，那么我们就认为它们是 叶相似 的。

如果给定的两个根结点分别为 root1 和 root2 的树是叶相似的，则返回 true；否则返回 false 。

示例 1：

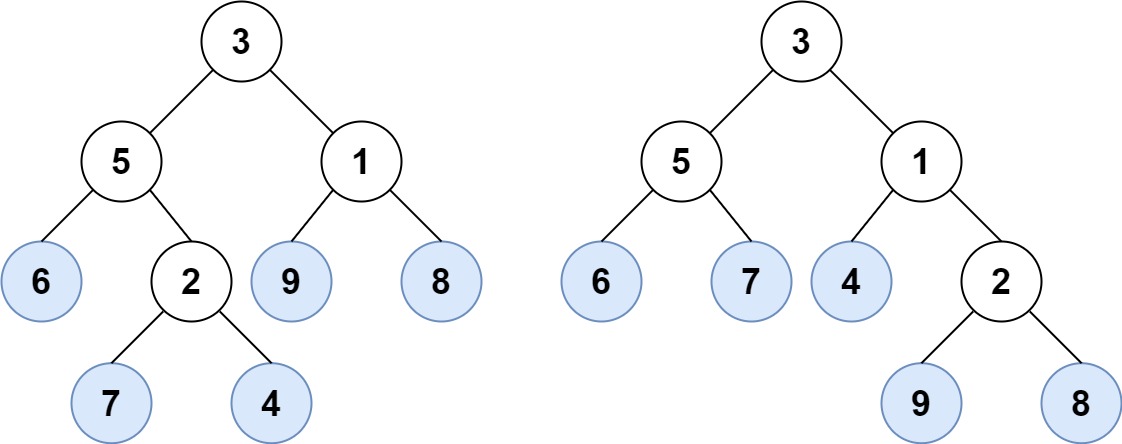
输入：root1 = [3,5,1,6,2,9,8,null,null,7,4], root2 = [3,5,1,6,7,4,2,null,null,null,null,null,null,9,8]
输出：true

示例 2：

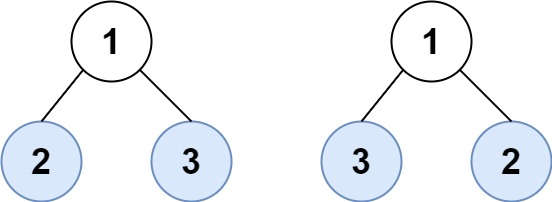
输入：root1 = [1,2,3], root2 = [1,3,2]
输出：false

提示：

• 给定的两棵树结点数在 [1, 200] 范围内
• 给定的两棵树上的值在 [0, 200] 范围内

思路

1. 直接考虑深度优先搜索，都会先遍历完左子树再遍历右子树，所以结果的顺序是符合要求的。只有叶节点会将自己的值返回，其他节点只接收子节点返回的vector数组。
2. 最后比较两个树的叶节点序列即可。

代码实现

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    vector<int> leaf_list(TreeNode* root) {
        vector<int> leaves, tmp;
        if(root->left==nullptr && root->right==nullptr) return {root->val}; 
        if(root->left != nullptr) {
            tmp = leaf_list(root->left);
            leaves.insert(leaves.end(), tmp.begin(), tmp.end());
        }
        if(root->right != nullptr) {
            // 这里的赋值是传指针，需判断函数结束是否会导致栈丢失，或用assign
            tmp = leaf_list(root->right);
            leaves.insert(leaves.end(), tmp.begin(), tmp.end());
        }
        return leaves;
    }
    bool leafSimilar(TreeNode* root1, TreeNode* root2) {
        vector<int> ls1, ls2;
        ls1 = leaf_list(root1);
        ls2 = leaf_list(root2);
        return (ls1==ls2);
    }
};

复杂度分析

• 时间复杂度：O(n1+n2)，要遍历两个数。
• 空间复杂度：取决于两个树的深搜的栈空间大小和叶子节点的数量的trade-off，不妨近似为O(n1+n2)（只知道这个松的上界，如果有大神知道怎么表达紧的上界，麻烦评论区告诉我，万分感谢）

知识积累

• vector的赋值可以通过assign函数和swap函数来实现赋值替换。assign函数是先清空目的vector再将源vector的值插入，时间复杂度是线性的(O(n))；swap函数直接交换两个vector的头指针，时间是常数的(O(1))。
• 另外一个赋值行为可以通过等号实现，其实现为对函数的浅拷贝（传指针/传引用）。在本代码中赋值行为发生在函数返回的时候，我原先以为返回值的函数栈空间消失会导致浅拷贝失败，从而出错。后来查了一下发现C++11新支持了一种移动语义，在return的过程中传入的是右值引用，返回时调用vector的移动构造函数，将源vector的迭代器拷贝给b，再释放a，所以不影响最终结果，（但是为了安全性，最好还是用上面吧，毕竟赋值逻辑什么时候会改不知道，但是函数功能一般不会改）。