深入理解逻辑回归：原理、优化与应用-优快云博客

本文链接：https://blog.youkuaiyun.com/X_harper/article/details/88944426

本文详细介绍了逻辑回归与线性回归的区别，包括适用条件和模型形式。接着，阐述了逻辑回归的原理，利用sigmoid函数将线性回归结果转化为概率，并通过最大似然法推导出损失函数及其优化过程。此外，讨论了正则化方法（L1和L2）、模型评估指标（如ROC曲线、AUC、Kappa等）以及如何应对样本不均衡问题。最后，探讨了逻辑回归的优缺点，并介绍了sklearn中LogisticRegression的参数设置。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

1、逻辑回归与线性回归的联系与区别

1）线性回归要求变量服从正态分布，logistic回归对变量分布没有要求。
2）线性回归要求因变量是连续性数值变量，而logistic回归要求因变量是分类型变量。
3）线性回归要求自变量和因变量呈线性关系，而logistic回归不要求自变量和因变量呈线性关系
4）logistic回归是分析因变量取某个值的概率与自变量的关系，而线性回归是直接分析因变量与自变量的关系
总之,
logistic回归与线性回归实际上有很多相同之处，最大的区别就在于他们的因变量不同，其他的基本都差不多，正是因为如此，这两种回归可以归于同一个家族，即广义线性模型（generalized linear model）。这一家族中的模型形式基本上都差不多，不同的就是因变量不同，如果是连续的，就是多重线性回归，如果是二项分布，就是logistic回归。logistic回归的因变量可以是二分类的，也可以是多分类的，但是二分类的更为常用，也更加容易解释。所以实际中最为常用的就是二分类的logistic回归。

2、逻辑回归的原理

线性回归的结果做一个在函数g上的转换，可以变化为逻辑回归。这个函数g在逻辑回归中我们一般取为sigmoid函数，形式如下：
在这里插入图片描述
它有一个非常好的性质，即当z趋于正无穷时，g(z)g(z)趋于1，而当z趋于负无穷时，g(z)g(z)趋于0，这非常适合于我们的分类概率模型。另外，它还有一个很好的导数性质：

这个通过函数对g(z)g(z)求导很容易得到，后面我们会用到这个式子。
如果我们令g(z)g(z)中的z为：z=xθz=xθ，这样就得到了二元逻辑回归模型的一般形式：
在这里插入图片描述
其中x为样本输入，hθ(x)hθ(x)为模型输出，可以理解为某一分类的概率大小。而θ为分类模型的要求出的模型参数。对于模型输出h_θ(x)，我们让它和我们的二元样本输出y（假设为0和1）有这样的对应关系，如果h_θ(x)>0.5 ，即x_θ>0, 则y为1。如果h_θ(x)<0.5h_θ(x)<0.5，即x_θ<0, 则y为0。y=0.5是临界情况，此时x_θ=0为，从逻辑回归模型本身无法确定分类。
h_θ(x)的值越小，而分类为0的的概率越高，反之，值越大的话分类为1的的概率越高。如果靠近临界点，则分类准确率会下降。
此处我们也可以将模型写成矩阵模式：
在这里插入图片描述
其中h_θ(X)为模型输出，为 mx1的维度。X为样本特征矩阵，为mxn的维度。θ为分类的模型系数，为nx1的向量。

3、逻辑回归损失函数推导及优化

损失函数的推导:
由于线性回归是连续的，所以可以使用模型误差的的平方和来定义损失函数。但是逻辑回归不是连续的，自然线性回归损失函数定义的经验就用不上了。不过我们可以用最大似然法来推导出我们的损失函数。
我们知道，按照第二节二元逻辑回归的定义，假设我们的样本输出是0或者1两类。那么我们有：

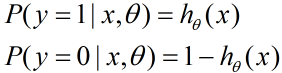
在这里插入图片描述
把这两个式子写成一个式子，就是：

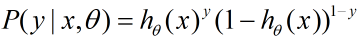
其中y的取值只能是0或者1。
得到了y的概率分布函数表达式，我们就可以用似然函数最大化来求解我们需要的模型系数θ。
为了方便求解，这里我们用对数似然函数最大化，对数似然函数取反即为我们的损失函数J(θ)。其中似然函数的代数表达式为：
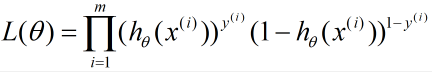
在这里插入图片描述
其中m为样本的个数。
对似然函数对数化取反的表达式，即损失函数表达式为：

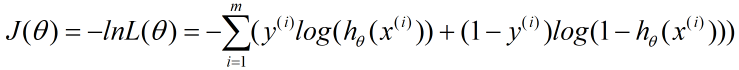
损失函数的优化
对于二元逻辑回归的损失函数极小化，有比较多的方法，最常见的有梯度下降法，坐标轴下降法，等牛顿法等。这里推导出梯度下降法中θ每次迭代的公式。由于代数法推导比较的繁琐，我习惯于用矩阵法来做损失函数的优化过程，这里给出矩阵法推导二元逻辑回归梯度的过程。
对于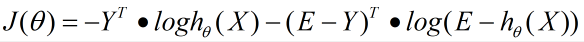
我们用J(θ)对θ向量求导可得：

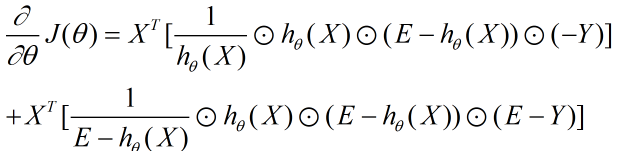
这一步我们用到了向量求导的链式法则，和下面三个基础求导公式的矩阵形式：

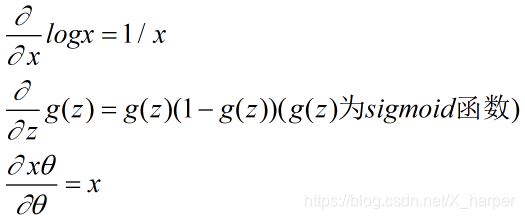
在这里插入图片描述
对于刚才的求导公式我们进行化简可得：

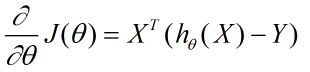
从而在梯度下降法中每一步向量θ的迭代公式如下：

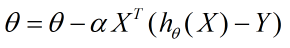
其中，α为梯度下降法的步长。

4、正则化与模型评估指标

正则化
逻辑回归也会面临过拟合问题，所以我们也要考虑正则化。常见的有L1正则化和L2正则化。
逻辑回归的L1正则化的损失函数表达式如下，相比普通的逻辑回归损失函数，增加了L1的范数做作为惩罚，超参数αα作为惩罚系数，调节惩罚项的大小。
二元逻辑回归的L1正则化损失函数表达式如下：

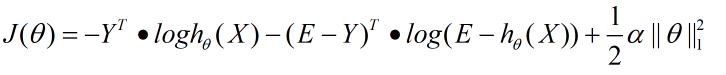
其中||θ||₁为θ的L1范数。
逻辑回归的L1正则化损失函数的优化方法常用的有坐标轴下降法和最小角回归法。
二元逻辑回归的L2正则化损失函数表达式如下：

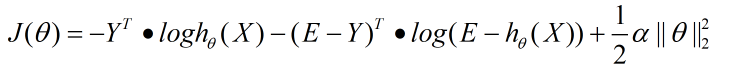
其中||θ||₂为θ的L2范数。
逻辑回归的L2正则化损失函数的优化方法和普通的逻辑回归类似。
评估指标
ROC曲线、AUC
ROC曲线的横坐标为false positive rate（FPR），纵坐标为 true positive rate（TPR）
当测试集中的正负样本的分布变化的时候，ROC曲线能够保持不变。根据每个测试样本属于正样本的概率值从大到小排序，依次将 “Score”值作为阈值threshold，当测试样本属于正样本的概率大于或等于这个threshold时，认为它为正样本，否则为负样本。
**Kappa statics **
Kappa值，即内部一致性系数(inter-rater,coefficient of internal consistency)，是作为评价判断的一致性程度的重要指标。取值在0～1之间。Kappa≥0.75两者一致性较好；0.75>Kappa≥0.4两者一致性一般；Kappa<0.4两者一致性较差
**Mean absolute error 和 Root mean squared error **
平均绝对误差和均方根误差，用来衡量分类器预测值和实际结果的差异，越小越好。
**Relative absolute error 和 Root relative squared error **
相对绝对误差和相对均方根误差，有时绝对误差不能体现误差的真实大小，而相对误差通过体现误差占真值的比重来反映误差大小。

5、逻辑回归的优缺点

优点

Logistic 回归是一种被人们广泛使用的算法，因为它非常高效，不需要太大的计算量，又通俗易懂，不需要缩放输入特征，不需要任何调整，且很容易调整，并且输出校准好的预测概率。

与线性回归一样，当你去掉与输出变量无关的属性以及相似度高的属性时，logistic 回归效果确实会更好。因此特征处理在 Logistic 和线性回归的性能方面起着重要的作用。

Logistic 回归的另一个优点是它非常容易实现，且训练起来很高效。在研究中，我通常以 Logistic 回归模型作为基准，再尝试使用更复杂的算法。

由于其简单且可快速实现的原因，Logistic 回归也是一个很好的基准，你可以用它来衡量其他更复杂的算法的性能。

缺点
它的一个缺点就是我们不能用 logistic 回归来解决非线性问题，因为它的决策面是线性的。我们来看看下面的例子，两个类各有俩实例。
Logistic 回归并非最强大的算法之一，它可以很容易地被更为复杂的算法所超越。另一个缺点是它高度依赖正确的数据表示。
这意味着逻辑回归在你已经确定了所有重要的自变量之前还不会成为一个有用的工具。由于其结果是离散的，Logistic 回归只能预测分类结果。它同时也以其容易过拟合而闻名。

6、样本不均衡问题解决办法

1. 产生新数据型：过采样小样本(SMOTE)，欠采样大样本。

过采样是通过增加样本中小类样本的数据量来实现样本均衡。其中较为简单的方式是直接复制小类样本，形成数量上的均衡。这种方法实现简单，但会由于数据较为单一而容易造成过拟合。 SMOTE过采样算法: 针对少数类样本的xi，求出其k近邻。随机选取k紧邻中一个样本记为xn。生成一个0到1之间的随机数r，然后根据Xnew = xi + r * (xn - xi)生成新数据。也可通过经过改进的抽样的方法，在少数类中加入随机噪声等生成数据。
欠采样大样本是通过减少多数类样本的样本数量来实现样本均衡。其中比较简单直接的方法就是随机去掉一些数据来减少多数类样本的规模，但这种方法可能会丢失一些重要的信息。还有一种方法就是，假设少数类样本数量为N，那就将多数类样本分为N个簇，取每个簇的中心点作为多数类的新样本，再加上少数类的所有样本进行训练。这样就可以保证了多数类样本在特征空间的分布特性。

2. 对原数据的权值进行改变

通过改变多数类样本和少数类样本数据在训练时的权重来解决样本不均衡的问题，是指在训练分类器时，为少数类样本赋予更大的权值，为多数类样本赋予较小的权值。例如scikit-learn中的SVM算法，也称作penalized-SVM，可以手动设置权重。若选择balanced，则算法会设定样本权重与其对应的样本数量成反比。

3. 通过组合集成方法解决

通过训练多个模型的方式解决数据不均衡的问题，是指将多数类数据随机分成少数类数据的量N份，每一份与全部的少数类数据一起训练成为一个分类器，这样反复训练会生成很多的分类器。最后再用组合的方式(bagging或者boosting)对分类器进行组合，得到更好的预测效果。简单来说若是分类问题可采用投票法，预测问题可以采用平均值。这个解决方式需要很强的计算能力以及时间，但效果较好，相当于结合了组合分类器的优势。

4. 通过特征选择

在样本数据较为不均衡，某一类别数据较少的情况下，通常会出现特征分布很不均衡的情况。例如文本分类中，有大量的特征可以选择。因此我们可以选择具有显著区分能力的特征进行训练，也能在一定程度上提高模型的泛化效果。

7. sklearn参数

class sklearn.linear_model.LogisticRegression(penalty=’l2’, dual=False, tol=0.0001, C=1.0, fit_intercept=True, intercept_scaling=1, class_weight=None,random_state=None, solver=’liblinear’, max_iter=100, multi_class=’ovr’, verbose=0, warm_start=False, n_jobs=1)
参数

penalty: 一个字符串，制定了正则化策略。
dual：一个布尔值。如果为True，则求解对偶形式（只是在penalty=‘l2’ 且solver=‘liblinear’ 有对偶形式）；如果为False，则求解原始形式。
C：一个浮点数，它指定了惩罚系数的倒数。如果它的值越小，则正则化越大。
fit_intercept：一个布尔值，制定是否需要b 值。如果为False，则不会计算b值（模型会假设你的数据已经中心化）。
intercept_scaling：一个浮点数，只有当solver=‘liblinear’ 才有意义。当采用 fit_intercept 时，相当于人造一个特征出来，该特征恒为 1，其权重为b 。在计算正则化项的时候，该人造特征也被考虑了。因此为了降低人造特征的影响，需要提供 intercept_scaling。
class_weight：一个字典或者字符串’balanced’。如果为字典：则字典给出了每个分类的权重，如{class_label:weight}。如果为字符串 ‘balanced’：则每个分类的权重与该分类在样品中出现的频率成反比。如果未指定，则每个分类的权重都为 1。
max_iter：一个整数，指定最大迭代数
random_state：一个整数或者一个RandomState实例，或者None。如果为整数，则它指定了随机数生成器的种子。如果为RandomState实例，则指定了随机数生成器。如果为None，则使用默认的随机数生成器。
solver：一个字符串，指定了求解最优化问题的算法，可以为如下的值。‘newton-cg’：使用牛顿法。‘lbfgs’：使用L-BFGS拟牛顿法。‘liblinear’ ：使用 liblinear。‘sag’：使用 Stochastic Average Gradient descent 算法。
tol：一个浮点数，指定判断迭代收敛与否的一个阈值。
multi_class：一个字符串，指定对于多分类问题的策略，可以为如下的值。‘ovr’
：采用 one-vs-rest 策略。‘multinomial’：直接采用多分类逻辑回归策略。
verbose：一个正数。用于开启/关闭迭代中间输出的日志。
warm_start：一个布尔值。如果为True，那么使用前一次训练结果继续训练，否则从头开始训练。
n_jobs：一个正数。指定任务并行时的 CPU 数量。如果为 -1 则使用所有了用的 CPU。
返回值
coef_：权重向量。
intercept：b值。
n_iter_：实际迭代次数。
方法
fix(X,y[,sample_weight])：训练模型。
predict(X)：用模型进行预测，返回预测值。
score(X,y[,sample_weight])：返回（X，y）上的预测准确率（accuracy）。
predict_log_proba（X）：返回一个数组，数组的元素一次是 X 预测为各个类别的概率的对数值。
predict_proba（X）：返回一个数组，数组元素一次是 X 预测为各个类别的概率的概率值。
sparsify()：将系数矩阵转换为稀疏格式。
set_params（**params）：设置此估计器的参数。
decision_function（X）：预测样本的置信度分数。
densify()：将系数矩阵转换为密集阵列格式。