44.【必备】前缀树的相关题目

于 2025-04-29 10:00:00 发布
阅读量982 收藏 14
点赞数 14
CC 4.0 BY-SA版权
分类专栏： 数据结构与算法 文章标签： 算法 java 数据结构
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.youkuaiyun.com/XY_StarField/article/details/147573231

本文的网课内容学习自B站左程云老师的算法详解课程，旨在对其中的知识进行整理和分享~

网课链接：算法讲解045【必备】前缀树的相关题目_哔哩哔哩_bilibili

一.接头秘钥

题目：接头密匙

算法原理

  • 整体原理
    • 这个算法的目的是找出给定的多个密匙b与多个密匙a中一致的密匙数量。为了高效地进行比较，算法使用了前缀树（Trie树）结构。将密匙a中的差值序列构建成前缀树，然后对于每个密匙b，计算其差值序列在前缀树中的出现次数，以此得到每个密匙b与密匙a一致的数量。
  • 具体步骤
  • 第一步：数据结构初始化。
    • 定义了一些静态变量用于构建前缀树：MAXN用于确定前缀树节点数组的大小；tree是一个二维数组，tree[i][j]表示第i个节点的第j个孩子节点的索引；pass数组，pass[i]表示经过第i个节点的字符串数量；cnt用于记录当前节点的数量，初始值为1，通过build方法将cnt初始化为1来初始化前缀树结构。
  • 第二步：构建密匙a的差值序列前缀树。
    • 在countConsistentKeys方法中，首先调用build方法初始化前缀树。
    • 对于每个密匙a中的数组nums，使用StringBuilder构建其差值序列的字符串表示。通过循环for (int i = 1; i < nums.length; i++)计算相邻元素的差值，并将差值和#符号添加到StringBuilder中。
    • 然后将这个差值序列字符串插入到前缀树中，通过insert方法实现。在insert方法中，从根节点（索引为1）开始，先将根节点的pass值加1，表示有一个新的字符串要插入。
    • 对于字符串中的每个字符，通过path方法将字符转换为对应的索引（0 - 9对应数字字符，10对应#，11对应-），如果当前节点的对应子节点不存在（tree[cur][path] == 0），则创建一个新的节点（tree[cur][path] = ++cnt），然后将当前节点移动到该子节点（cur = tree[cur][path]），并将该子节点的pass值加1。
  • 第三步：计算密匙b与密匙a一致的数量。
    • 创建一个结果数组ans，长度为密匙b的数量。
    • 对于每个密匙b中的数组nums，同样使用StringBuilder构建其差值序列的字符串表示。
    • 然后调用count方法，在前缀树中查找该差值序列字符串的出现次数，并将结果存储到ans数组中。在count方法中，从根节点开始，对于字符串中的每个字符，通过path方法得到索引，若当前节点的对应子节点不存在（tree[cur][path] = 0），则返回0，表示该差值序列不存在于前缀树中；如果能够顺利遍历完整个字符串，则返回最后一个节点的pass值，即该差值序列在前缀树中的出现次数。
  • 第四步：清除前缀树。
    • 最后调用clear方法，通过循环遍历从1到cnt的所有节点，使用Arrays.fill将tree[i]数组中的所有元素设置为0，将pass[i]设置为0，以清除前缀树中的所有数据，为下一次操作做准备。

代码实现

import java.util.Arrays;

// 牛牛和他的朋友们约定了一套接头密匙系统，用于确认彼此身份
// 密匙由一组数字序列表示，两个密匙被认为是一致的，如果满足以下条件：
// 密匙 b 的长度不超过密匙 a 的长度。
// 对于任意 0 <= i < length(b)，有b[i+1] - b[i] == a[i+1] - a[i]
// 现在给定了m个密匙 b 的数组，以及n个密匙 a 的数组
// 请你返回一个长度为 m 的结果数组 ans，表示每个密匙b都有多少一致的密匙
// 数组 a 和数组 b 中的元素个数均不超过 10^5
// 1 <= m, n <= 1000
// 测试链接 : https://www.nowcoder.com/practice/c552d3b4dfda49ccb883a6371d9a6932
public class Code01_CountConsistentKeys {

    public static int[] countConsistentKeys(int[][] b, int[][] a) {
        build();
        StringBuilder builder = new StringBuilder();
        // [3,6,50,10] -> "3#44#-40#"
        for (int[] nums : a) {
            builder.setLength(0);
            for (int i = 1; i < nums.length; i++) {
                builder.append(String.valueOf(nums[i] - nums[i - 1]) + "#");
            }
            insert(builder.toString());
        }
        int[] ans = new int[b.length];
        for (int i = 0; i < b.length; i++) {
            builder.setLength(0);
            int[] nums = b[i];
            for (int j = 1; j < nums.length; j++) {
                builder.append(String.valueOf(nums[j] - nums[j - 1]) + "#");
            }
            ans[i] = count(builder.toString());
        }
        clear();
        return ans;
    }

    // 如果将来增加了数据量，就改大这个值
    public static int MAXN = 2000001;

    public static int[][] tree = new int[MAXN][12];

    public static int[] pass = new int[MAXN];

    public static int cnt;

    public static void build() {
        cnt = 1;
    }

    // '0' ~ '9' 10个 0~9
    // '#' 10
    // '-' 11
    public static int path(char cha) {
        if (cha == '#') {
            return 10;
        } else if (cha == '-') {
            return 11;
        } else {
            return cha - '0';
        }
    }

    public static void insert(String word) {
        int cur = 1;
        pass[cur]++;
        for (int i = 0, path; i < word.length(); i++) {
            path = path(word.charAt(i));
            if (tree[cur][path] == 0) {
                tree[cur][path] = ++cnt;
            }
            cur = tree[cur][path];
            pass[cur]++;
        }
    }

    public static int count(String pre) {
        int cur = 1;
        for (int i = 0, path; i < pre.length(); i++) {
            path = path(pre.charAt(i));
            if (tree[cur][path] == 0) {
                return 0;
            }
            cur = tree[cur][path];
        }
        return pass[cur];
    }

    public static void clear() {
        for (int i = 1; i <= cnt; i++) {
            Arrays.fill(tree[i], 0);
            pass[i] = 0;
        }
    }

}

二.数组中两个数的最大异或值

题目：数组中两个数的最大异或值

算法原理

  • 整体原理
    • 这个代码主要解决了在给定整数数组中找出两个数的最大异或值的问题。提供了两种方法，一种是基于前缀树（Trie树）的方法，另一种是基于哈希表的方法。
  • 基于前缀树方法（findMaximumXOR1等相关方法）的原理
    • 第一步：构建前缀树（build方法）。
      • 首先确定要考虑的最高有效位（high）。通过找到数组中的最大值max，然后计算其最高有效位。具体是用31 - Integer.numberOfLeadingZeros(max)，即31减去最大值二进制表示中前导零的数量。
      • 然后将每个数插入到前缀树中。从根节点（索引为1）开始，对于每个数num，通过循环从最高有效位high到0，获取当前位的值path=(num >> i)&1（右移i位后取最低位）。如果当前节点的对应子节点不存在（tree[cur][path] == 0），则创建一个新的节点（tree[cur][path]=++cnt），然后将当前节点移动到该子节点（cur = tree[cur][path]）。
    • 第二步：计算最大异或值（findMaximumXOR1方法）。
      • 遍历数组中的每个数num，对于每个数调用maxXor方法计算其与其他数的最大异或值，并更新全局最大异或值ans。
    • 第三步：maxXor方法原理。
      • 对于给定的数num，从最高有效位high开始遍历到0位。计算当前位的状态status=(num >> i)&1，希望遇到的状态want = status^1（因为异或1可以使该位取反，这样有可能得到更大的异或值）。
      • 如果在当前节点cur下，希望的路径tree[cur][want]不存在，则只能选择另一个状态（want^ = 1）。
      • 然后更新异或结果ans，将当前位的异或结果(status^want)<<i与之前的结果ans进行或操作（ans|=(status^want)<<i），最后将当前节点移动到选择的子节点（cur = tree[cur][want]）。
    • 第四步：清除前缀树（clear方法）。
      • 遍历从1到cnt的所有节点，将每个节点的两个子节点（对应0和1的子节点）都设置为0，以清除前缀树结构。
  • 基于哈希表方法（findMaximumXOR2方法）的原理
    • 首先找到数组中的最大值max，确定要从哪一位开始考虑（31 - Integer.numberOfLeadingZeros(max)）。
    • 初始化最大异或值ans = 0。然后从最高有效位开始，每次尝试将ans的下一位设置为1（better = ans|(1 << i)），构建一个HashSet。
    • 对于数组中的每个数num，将其高位部分保留（num=(num >> i)<<i）并加入到HashSet中。然后检查是否存在某个数num，使得num与better ^ num在HashSet中，即是否存在两个数异或可以得到better。如果存在，则更新ans = better并跳出内层循环。最后返回ans，即为数组中两个数的最大异或值。

代码实现

import java.util.HashSet;

// 数组中两个数的最大异或值
// 给你一个整数数组 nums ，返回 nums[i] XOR nums[j] 的最大运算结果，其中 0<=i<=j<=n
// 1 <= nums.length <= 2 * 10^5
// 0 <= nums[i] <= 2^31 - 1
// 测试链接 : https://leetcode.cn/problems/maximum-xor-of-two-numbers-in-an-array/
public class Code02_TwoNumbersMaximumXor {

    // 前缀树的做法
    // 好想
    public static int findMaximumXOR1(int[] nums) {
        build(nums);
        int ans = 0;
        for (int num : nums) {
            ans = Math.max(ans, maxXor(num));
        }
        clear();
        return ans;
    }

    // 准备这么多静态空间就够了，实验出来的
    // 如果测试数据升级了规模，就改大这个值
    public static int MAXN = 3000001;

    public static int[][] tree = new int[MAXN][2];

    // 前缀树目前使用了多少空间
    public static int cnt;

    // 数字只需要从哪一位开始考虑
    public static int high;

    public static void build(int[] nums) {
        cnt = 1;
        // 找个最大值
        int max = Integer.MIN_VALUE;
        for (int num : nums) {
            max = Math.max(num, max);
        }
        // 计算数组最大值的二进制状态，有多少个前缀的0
        // 可以忽略这些前置的0，从left位开始考虑
        high = 31 - Integer.numberOfLeadingZeros(max);
        for (int num : nums) {
            insert(num);
        }
    }

    public static void insert(int num) {
        int cur = 1;
        for (int i = high, path; i >= 0; i--) {
            path = (num >> i) & 1;
            if (tree[cur][path] == 0) {
                tree[cur][path] = ++cnt;
            }
            cur = tree[cur][path];
        }
    }

    public static int maxXor(int num) {
        // 最终异或的结果(尽量大)
        int ans = 0;
        // 前缀树目前来到的节点编号
        int cur = 1;
        for (int i = high, status, want; i >= 0; i--) {
            // status : num第i位的状态
            status = (num >> i) & 1;
            // want : num第i位希望遇到的状态
            want = status ^ 1;
            if (tree[cur][want] == 0) { // 询问前缀树，能不能达成
                // 不能达成
                want ^= 1;
            }
            // want变成真的往下走的路
            ans |= (status ^ want) << i;
            cur = tree[cur][want];
        }
        return ans;
    }

    public static void clear() {
        for (int i = 1; i <= cnt; i++) {
            tree[i][0] = tree[i][1] = 0;
        }
    }

    // 用哈希表的做法
    // 难想
    public int findMaximumXOR2(int[] nums) {
        int max = Integer.MIN_VALUE;
        for (int num : nums) {
            max = Math.max(num, max);
        }
        int ans = 0;
        HashSet<Integer> set = new HashSet<>();
        for (int i = 31 - Integer.numberOfLeadingZeros(max); i >= 0; i--) {
            // ans : 31....i+1 已经达成的目标
            int better = ans | (1 << i);
            set.clear();
            for (int num : nums) {
                // num : 31.....i 这些状态保留，剩下全成0
                num = (num >> i) << i;
                set.add(num);
                // num ^ 某状态 是否能 达成better目标，就在set中找 某状态 : better ^ num
                if (set.contains(better ^ num)) {
                    ans = better;
                    break;
                }
            }
        }
        return ans;
    }

}

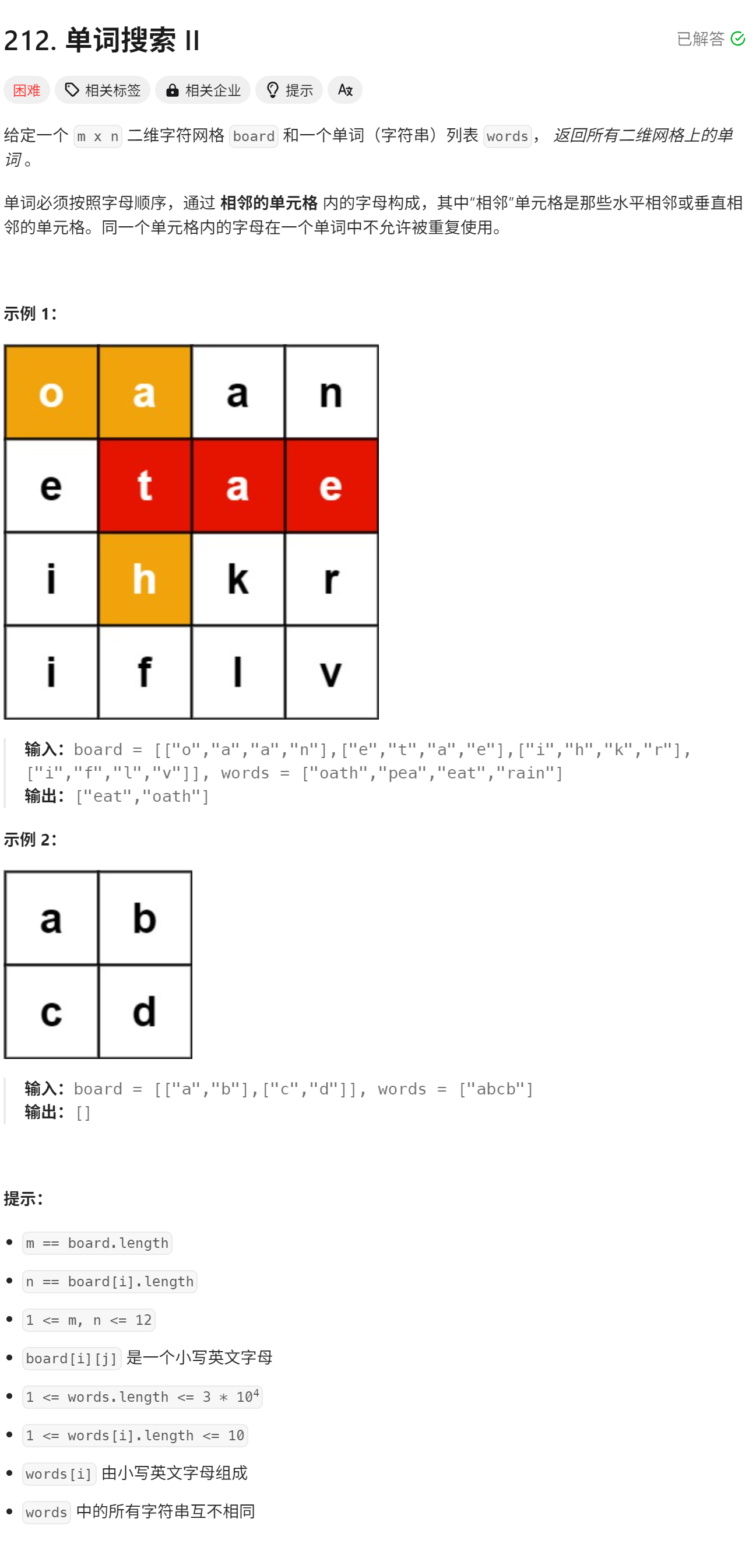
 三.单词搜索 II

题目：单词搜索 II

算法原理

  • 整体原理
    • 这个算法主要解决在给定的二维字符网格board中搜索出单词列表words里存在的单词的问题。它使用了前缀树（Trie树）结构来高效地查找单词，并结合深度优先搜索（DFS）算法在二维网格中进行遍历查找。
  • 具体步骤
    • 第一步：构建前缀树（build方法）。
      • 首先初始化前缀树的根节点索引为1（cnt = 1）。
      • 然后遍历单词列表words中的每个单词word。对于每个单词，从根节点（索引为1）开始，先将根节点的pass值加1，表示有一个新的单词要插入到前缀树相关的结构中。
      • 接着遍历单词中的每个字符，通过path = word.charAt(i) - 'a'计算出在tree数组中的列索引（将字符转换为对应的数组下标，假设只处理小写字母，每个位置对应一个字母，例如tree[cur][0]对应a的子节点）。
      • 如果当前节点（cur）的tree[cur][path]为0，表示该字符对应的子节点不存在，那么创建一个新的节点（tree[cur][path]=++cnt）。
      • 然后将当前节点移动到该子节点（cur = tree[cur][path]），并将该子节点的pass值加1。
      • 当遍历完整个单词后，将最后一个节点的end属性设置为该单词（end[cur]=word），用于标记以该节点为结尾的单词。
    • 第二步：在二维网格中搜索单词（findWords方法）。
      • 创建一个结果列表ans用于存储找到的单词。
      • 然后通过两层循环遍历二维网格board的每一个单元格（i表示行，j表示列）。
      • 对于每个单元格，调用dfs方法进行深度优先搜索，传入当前单元格的坐标i、j，初始前缀树节点索引1，以及结果列表ans。
    • 第三步：深度优先搜索（dfs方法）。
      • 首先进行边界条件判断，如果当前单元格的坐标i、j越界（i < 0 || i == board.length || j < 0 || j == board[0].length）或者该单元格已经被访问过（board[i][j] == 0），则直接返回0，表示没有找到单词。
      • 如果当前单元格有效，获取该单元格的字符tmp = board[i][j]，并计算出在前缀树中的路径索引road = tmp - 'a'。
      • 根据当前前缀树节点索引t和路径索引road找到下一个前缀树节点索引t = tree[t][road]，如果该节点的pass值为0，表示没有单词经过该节点，直接返回0。
      • 如果当前节点有效，初始化一个变量fix = 0用于记录从当前位置出发找到的单词数量。
      • 如果当前节点的end属性不为空，表示找到了一个完整的单词，将fix加1，把该单词添加到结果列表ans中，并将end[t]设置为null，避免重复添加。
      • 然后将当前单元格标记为已访问（board[i][j]=0），防止在本次搜索中再次访问该单元格。
      • 接着分别向上（i - 1）、向下（i + 1）、向左（j - 1）、向右（j + 1）四个方向进行递归调用dfs方法，并将返回值累加到fix中。
      • 之后更新当前前缀树节点的pass值（pass[t]-=fix），表示经过该节点的单词数量减少了fix个。
      • 最后恢复当前单元格的值（board[i][j]=tmp），并返回fix，表示从当前位置出发找到的单词数量。
    • 第四步：清除前缀树（clear方法）。
      • 遍历从1到cnt的所有节点，对于每个节点，使用Arrays.fill将tree[i]数组中的所有元素设置为0，将pass[i]设置为0，将end[i]设置为null，以清除前缀树中的所有数据，为下一次操作做准备。

代码实现

import java.util.ArrayList;
import java.util.Arrays;
import java.util.List;

// 在二维字符数组中搜索可能的单词
// 给定一个 m x n 二维字符网格 board 和一个单词（字符串）列表 words
// 返回所有二维网格上的单词。单词必须按照字母顺序，通过 相邻的单元格 内的字母构成
// 其中“相邻”单元格是那些水平相邻或垂直相邻的单元格
// 同一个单元格内的字母在一个单词中不允许被重复使用
// 1 <= m, n <= 12
// 1 <= words.length <= 3 * 10^4
// 1 <= words[i].length <= 10
// 测试链接 : https://leetcode.cn/problems/word-search-ii/
public class Code03_WordSearchII {

    public static List<String> findWords(char[][] board, String[] words) {
        build(words);
        List<String> ans = new ArrayList<>();
        for (int i = 0; i < board.length; i++) {
            for (int j = 0; j < board[0].length; j++) {
                dfs(board, i, j, 1, ans);
            }
        }
        clear();
        return ans;
    }

    // board : 二维网格
    // i,j : 此时来到的格子位置，i行、j列
    // t : 前缀树的编号
    // List<String> ans : 收集到了哪些字符串，都放入ans
    // 返回值 : 收集到了几个字符串
    public static int dfs(char[][] board, int i, int j, int t, List<String> ans) {
        // 越界 或者 走了回头路，直接返回0
        if (i < 0 || i == board.length || j < 0 || j == board[0].length || board[i][j] == 0) {
            return 0;
        }
        // 不越界 且 不是回头路
        // 用tmp记录当前字符
        char tmp = board[i][j];
        // 路的编号
        // a -> 0
        // b -> 1
        // ...
        // z -> 25
        int road = tmp - 'a';
        t = tree[t][road];
        if (pass[t] == 0) {
            return 0;
        }
        // i，j位置有必要来
        // fix ：从当前i，j位置出发，一共收集到了几个字符串
        int fix = 0;
        if (end[t] != null) {
            fix++;
            ans.add(end[t]);
            end[t] = null;
        }
        // 把i，j位置的字符，改成0，后续的过程，是不可以再来到i，j位置的！
        board[i][j] = 0;
        fix += dfs(board, i - 1, j, t, ans);
        fix += dfs(board, i + 1, j, t, ans);
        fix += dfs(board, i, j - 1, t, ans);
        fix += dfs(board, i, j + 1, t, ans);
        pass[t] -= fix;
        board[i][j] = tmp;
        return fix;
    }

    public static int MAXN = 10001;

    public static int[][] tree = new int[MAXN][26];

    public static int[] pass = new int[MAXN];

    public static String[] end = new String[MAXN];

    public static int cnt;

    public static void build(String[] words) {
        cnt = 1;
        for (String word : words) {
            int cur = 1;
            pass[cur]++;
            for (int i = 0, path; i < word.length(); i++) {
                path = word.charAt(i) - 'a';
                if (tree[cur][path] == 0) {
                    tree[cur][path] = ++cnt;
                }
                cur = tree[cur][path];
                pass[cur]++;
            }
            end[cur] = word;
        }
    }

    public static void clear() {
        for (int i = 1; i <= cnt; i++) {
            Arrays.fill(tree[i], 0);
            pass[i] = 0;
            end[i] = null;
        }
    }

}

 

评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值