51.【必备】单调栈-上

最新推荐文章于 2025-12-05 23:25:47 发布
原创 最新推荐文章于 2025-12-05 23:25:47 发布 · 1.7k 阅读 · 43 ·
CC 4.0 BY-SA版权
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
文章标签：

#数据结构 #算法 #单调栈 #java

本文的网课内容学习自B站左程云老师的算法详解课程，旨在对其中的知识进行整理和分享~

网课链接：算法讲解052【必备】单调栈-上_哔哩哔哩_bilibili

一.单调栈结构

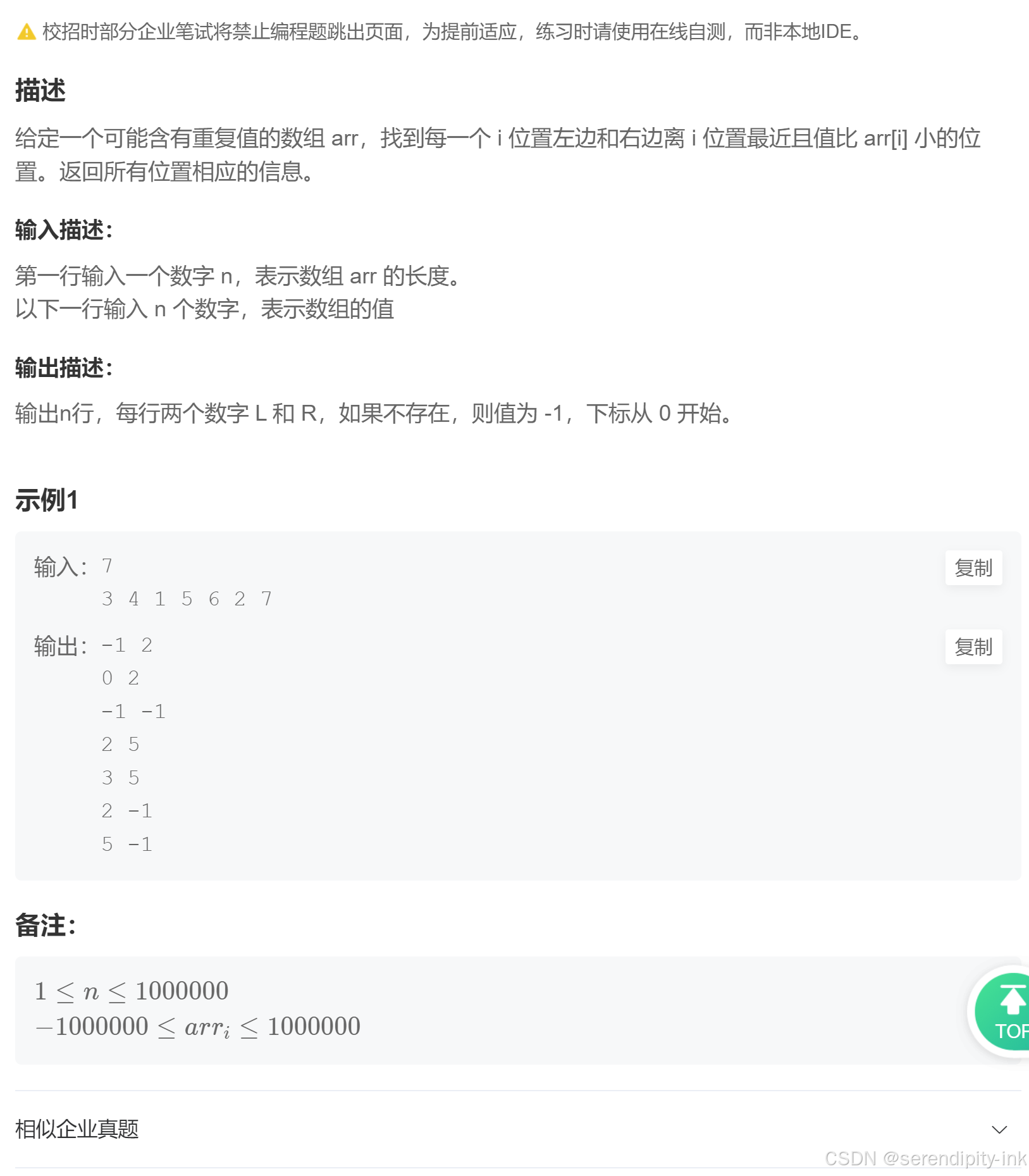
题目：单调栈结构(进阶)

算法原理

  • 单调栈的基本概念
    • 单调栈是一种特殊的数据结构，在这个问题中，我们使用单调递增栈（栈顶到栈底元素值单调递增）。
    • 它的主要作用是在一次遍历中高效地找到每个元素左右两侧满足特定条件（比当前元素值小）的元素位置。
  • 算法的遍历阶段（compute函数中的第一个循环）
    • 当遍历数组arr时，对于每个元素arr[i]：
      • 只要栈不为空（r > 0）并且栈顶元素对应的数组值arr[stack[r - 1]]大于等于arr[i]，就弹出栈顶元素。
      • 对于弹出的元素cur = stack[--r]：
        • 计算其左边最近且值比arr[cur]小的位置，如果栈不为空（r > 0），则是stack[r - 1]，否则是 -1。
        • 其右边最近且值比arr[cur]小的位置就是当前遍历到的i。
      • 然后将当前位置i压入栈中（stack[r++] = i）。
    • 这个过程实际上是在维护一个单调递增的栈，并且在弹出元素时，确定了该元素左右两侧满足条件的位置。
  • 算法的清算阶段（compute函数中的第二个循环）
    • 当遍历完整个数组后，栈中可能还剩余一些元素。
    • 对于这些剩余元素cur = stack[--r]：
      • 计算其左边最近且值比arr[cur]小的位置，如果栈不为空（r > 0），则是stack[r - 1]，否则是 -1。
      • 其右边最近且值比arr[cur]小的位置是 -1，因为这些元素是遍历完数组后栈中剩余的，右边没有更小的值了。
  • 算法的修正阶段（compute函数中的第三个循环）
    • 由于在前面的计算中，当右侧值相等时可能得到不准确的结果，所以需要从右往左修正右侧的答案。
    • 对于位置i（从n - 2到0）：
      • 如果ans[i][1]（右侧最近且小的位置）不为 -1并且arr[ans[i][1]]==arr[i]，这意味着右侧位置的值与当前位置的值相等。
      • 此时，将ans[i][1]更新为ans[ans[i][1]][1]，也就是右侧位置的右侧最近且小的位置，以得到准确的结果。

代码实现

// 单调栈求每个位置左右两侧，离当前位置最近、且值严格小于的位置
// 给定一个可能含有重复值的数组 arr
// 找到每一个 i 位置左边和右边离 i 位置最近且值比 arr[i] 小的位置
// 返回所有位置相应的信息。
// 输入描述：
// 第一行输入一个数字 n，表示数组 arr 的长度。
// 以下一行输入 n 个数字，表示数组的值
// 输出描述：
// 输出n行，每行两个数字 L 和 R，如果不存在，则值为 -1，下标从 0 开始。
// 测试链接 : https://www.nowcoder.com/practice/2a2c00e7a88a498693568cef63a4b7bb
// 请同学们务必参考如下代码中关于输入、输出的处理
// 这是输入输出处理效率很高的写法
// 提交以下的code，提交时请把类名改成"Main"，可以直接通过

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.io.OutputStreamWriter;
import java.io.PrintWriter;
import java.io.StreamTokenizer;

public class Code01_LeftRightLess {

    public static int MAXN = 1000001;

    public static int[] arr = new int[MAXN];

    public static int[] stack = new int[MAXN];

    public static int[][] ans = new int[MAXN][2];

    public static int n, r;

    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        StreamTokenizer in = new StreamTokenizer(br);
        PrintWriter out = new PrintWriter(new OutputStreamWriter(System.out));
        while (in.nextToken() != StreamTokenizer.TT_EOF) {
            n = (int) in.nval;
            for (int i = 0; i < n; i++) {
                in.nextToken();
                arr[i] = (int) in.nval;
            }
            compute();
            for (int i = 0; i < n; i++) {
                out.println(ans[i][0] + " " + ans[i][1]);
            }
        }
        out.flush();
        out.close();
        br.close();
    }

    // arr[0...n-1]
    public static void compute() {
        r = 0;
        int cur;
        // 遍历阶段
        for (int i = 0; i < n; i++) {
            // i -> arr[i]
            while (r > 0 && arr[stack[r - 1]] >= arr[i]) {
                cur = stack[--r];
                // cur当前弹出的位置，左边最近且小
                ans[cur][0] = r > 0 ? stack[r - 1] : -1;
                ans[cur][1] = i;
            }
            stack[r++] = i;
        }
        // 清算阶段
        while (r > 0) {
            cur = stack[--r];
            ans[cur][0] = r > 0 ? stack[r - 1] : -1;
            ans[cur][1] = -1;
        }
        // 修正阶段
        // 左侧的答案不需要修正一定是正确的，只有右侧答案需要修正
        // 从右往左修正，n-1位置的右侧答案一定是-1，不需要修正
        for (int i = n - 2; i >= 0; i--) {
            if (ans[i][1] != -1 && arr[ans[i][1]] == arr[i]) {
                ans[i][1] = ans[ans[i][1]][1];
            }
        }
    }

}

二.每日温度

题目：每日温度

算法原理

  • 整体思路
    • 这个算法主要利用了单调栈的思想来解决“每日温度”的问题。单调栈是一种特殊的数据结构，在这个算法中，栈中的元素索引对应的温度值是单调递增的。通过遍历温度数组，利用单调栈可以高效地找到每个温度下一个更高温度出现的天数间隔。
  • 算法步骤
    • 初始化
      • 定义了一个最大长度为MAXN = 100001的数组stack，用于存储温度数组的索引，r用于表示栈顶指针（初始化为0），同时创建一个与输入温度数组nums长度相同的结果数组ans，用于存储每个温度下一个更高温度出现的天数间隔，初始化为0。
    • 遍历温度数组nums（for循环）
      • 对于每个温度nums[i]：
        • 处理单调栈（while循环）
          • 当栈不为空（r > 0）并且栈顶元素对应的温度nums[stack[r - 1]]小于当前温度nums[i]时：
            • 弹出栈顶元素，将其索引存储在cur中（cur = stack[--r];）。
            • 计算当前温度nums[i]与弹出元素对应的温度nums[cur]的天数间隔，将其存储在结果数组ans中（ans[cur] = i - cur;）。这个间隔就是当前索引i减去弹出元素的索引cur。
        • 将当前索引i压入栈（stack[r++] = i;）
          • 无论是否弹出了栈顶元素，都将当前索引i压入栈中。如果没有弹出元素，说明当前温度nums[i]小于等于栈顶元素对应的温度，需要等待后续更高的温度来处理；如果弹出了元素，将当前索引压入栈后，栈仍然保持单调递增的性质。
    • 最终结果
      • 遍历完整个温度数组后，结果数组ans中存储了每个温度下一个更高温度出现的天数间隔，返回这个结果数组。

代码实现

// 每日温度
// 给定一个整数数组 temperatures ，表示每天的温度，返回一个数组 answer
// 其中 answer[i] 是指对于第 i 天，下一个更高温度出现在几天后
// 如果气温在这之后都不会升高，请在该位置用 0 来代替。
// 测试链接 : https://leetcode.cn/problems/daily-temperatures/
public class Code02_DailyTemperatures {

    public static int MAXN = 100001;

    public static int[] stack = new int[MAXN];

    public static int r;

    public static int[] dailyTemperatures(int[] nums) {
        int n = nums.length;
        int[] ans = new int[n];
        r = 0;
        for (int i = 0, cur; i < n; i++) {
            // 相等时候的处理，相等也加入单调栈
            while (r > 0 && nums[stack[r - 1]] < nums[i]) {
                cur = stack[--r];
                ans[cur] = i - cur;
            }
            stack[r++] = i;
        }
        return ans;
    }

}

 三.子数组的最小值之和

题目：子数组的最小值之和

算法原理

  • 整体思路
    • 这个算法利用单调栈来高效地计算给定数组所有连续子数组的最小值之和。通过维护一个单调栈（栈中元素对应的数组值单调递增），可以快速确定每个元素作为最小值的子数组的数量，进而计算出这些子数组最小值之和。
  • 算法步骤
    • 初始化
      • 定义了取模值MOD = 1000000007，栈的最大长度MAXN = 30001，用于存储数组索引的栈stack，栈顶指针r初始化为0，以及用于存储结果的ans初始化为0。
    • 遍历数组arr（外层for循环）
      • 对于数组中的每个元素arr[i]：
        • 处理单调栈（内层while循环）
          • 当栈不为空（r > 0）且栈顶元素对应的数组值arr[stack[r - 1]]大于等于arr[i]时：
            • 弹出栈顶元素，将其索引存储为cur（int cur = stack[--r];）。
            • 确定cur左边的索引left，如果r == 0，则left = -1，否则left = stack[r - 1];。
            • 计算以arr[cur]为最小值的子数组数量对结果的贡献，并累加到ans中。这个贡献的计算基于子数组的左右边界，即(cur - left)表示左边的子数组数量，(i - cur)表示右边的子数组数量，所以这部分子数组最小值之和为(cur - left) * (i - cur) * arr[cur]，然后将其对MOD取模后累加到ans（ans = (ans+(long)(cur - left) * (i - cur) * arr[cur]) % MOD;）。
        • 将当前索引i压入栈（stack[r++] = i;）
          • 无论是否弹出了栈顶元素，都将当前索引i压入栈中，以保持单调栈的性质，为后续元素的处理做准备。
    • 处理栈中剩余元素（外层while循环之后的while循环）
      • 当遍历完整个数组后，栈中可能还剩余一些元素。对于每个剩余元素cur（从栈顶开始依次处理）：
        • 同样确定cur左边的索引left，计算以arr[cur]为最小值的剩余子数组数量对结果的贡献，并累加到ans中。这里(cur - left)表示左边的子数组数量，(arr.length - cur)表示右边的子数组数量，所以这部分子数组最小值之和为(cur - left) * (arr.length - cur) * arr[cur]，然后将其对MOD取模后累加到ans（ans = (ans+(long)(cur - left) * (arr.length - cur) * arr[cur]) % MOD;）。
    • 最终结果
      • 最后将ans转换为int类型并返回，这个值就是所有连续子数组最小值之和对MOD取模的结果。

代码实现

// 子数组的最小值之和
// 给定一个整数数组 arr，找到 min(b) 的总和，其中 b 的范围为 arr 的每个（连续）子数组。
// 由于答案可能很大，答案对 1000000007 取模
// 测试链接 : https://leetcode.cn/problems/sum-of-subarray-minimums/
public class Code03_SumOfSubarrayMinimums {

    public static int MOD = 1000000007;

    public static int MAXN = 30001;

    public static int[] stack = new int[MAXN];

    public static int r;

    public static int sumSubarrayMins(int[] arr) {
        long ans = 0;
        r = 0;
        // 注意课上讲的相等情况的修正
        for (int i = 0; i < arr.length; i++) {
            while (r > 0 && arr[stack[r - 1]] >= arr[i]) {
                int cur = stack[--r];
                int left = r == 0 ? -1 : stack[r - 1];
                ans = (ans + (long) (cur - left) * (i - cur) * arr[cur]) % MOD;
            }
            stack[r++] = i;
        }
        while (r > 0) {
            int cur = stack[--r];
            int left = r == 0 ? -1 : stack[r - 1];
            ans = (ans + (long) (cur - left) * (arr.length - cur) * arr[cur]) % MOD;
        }
        return (int) ans;
    }

}

四.柱状图中最大的矩形

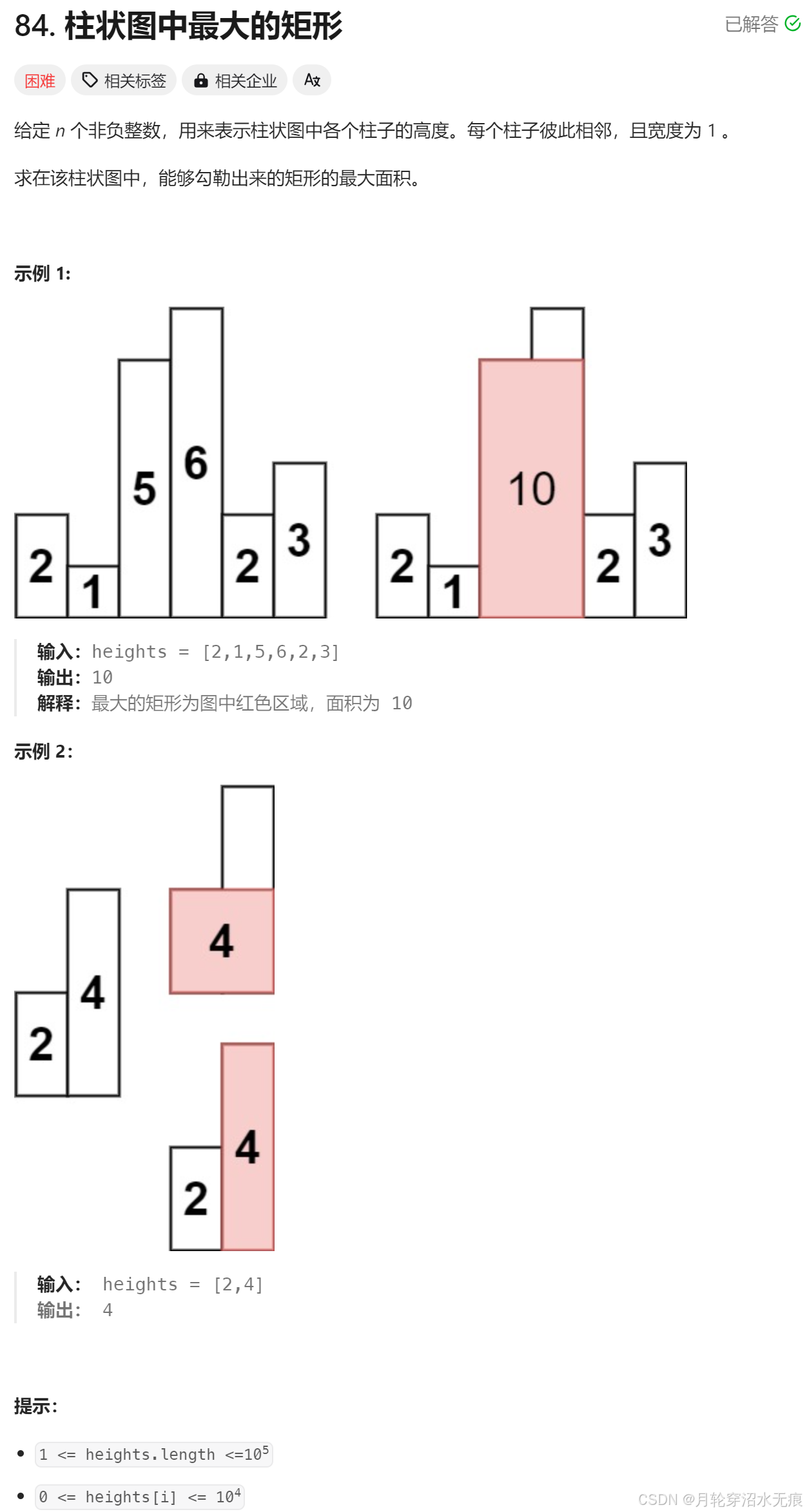
题目：柱状图中最大的矩形

算法原理

  • 整体思路
    • 这个算法主要利用单调栈的思想来求解柱状图中能够勾勒出的矩形的最大面积。通过维护一个单调栈（栈中元素对应的柱状高度单调递增），可以快速确定每个柱子作为矩形高度时，矩形的最大宽度，从而计算出最大面积。
  • 算法步骤
    • 初始化
      • 定义了栈的最大长度MAXN = 100001，用于存储柱子索引的栈stack，栈顶指针r初始化为0。同时定义变量ans用于存储最大矩形面积，初始值为0，还有用于临时存储栈顶元素索引的cur和栈顶元素左边索引的left。
    • 遍历高度数组（for循环）
      • 对于高度数组height中的每个元素height[i]：
        • 处理单调栈（while循环）
          • 当栈不为空（r > 0）且栈顶元素对应的高度height[stack[r - 1]]大于等于height[i]时：
            • 弹出栈顶元素，将其索引存储为cur（cur = stack[--r];）。
            • 确定cur左边的索引left，如果r == 0，则left = -1，否则left = stack[r - 1];。
            • 计算以height[cur]为高的矩形面积，宽度为i - left - 1（ans = Math.max(ans, height[cur] * (i - left - 1));）。
        • 将当前索引i压入栈（stack[r++] = i;）
          • 无论是否弹出了栈顶元素，都将当前索引i压入栈中，以保持单调栈的性质。
    • 处理栈中剩余元素（while循环）
      • 当遍历完整个高度数组后，栈中可能还剩余一些元素。对于每个剩余元素cur（从栈顶开始依次处理）：
        • 确定cur左边的索引left，计算以height[cur]为高的矩形面积，宽度为height.length - left - 1（ans = Math.max(ans, height[cur] * (n - left - 1));）。
    • 最终结果
      • 最后返回ans，这个值就是在给定柱状图中能够勾勒出来的矩形的最大面积。

代码实现

// 柱状图中最大的矩形
// 给定 n 个非负整数，用来表示柱状图中各个柱子的高度
// 每个柱子彼此相邻，且宽度为 1 。求在该柱状图中，能够勾勒出来的矩形的最大面积
// 测试链接：https://leetcode.cn/problems/largest-rectangle-in-histogram
public class Code04_LargestRectangleInHistogram {

    public static int MAXN = 100001;

    public static int[] stack = new int[MAXN];

    public static int r;

    public static int largestRectangleArea(int[] height) {
        int n = height.length;
        r = 0;
        int ans = 0, cur, left;
        for (int i = 0; i < n; i++) {
            // i -> arr[i]
            while (r > 0 && height[stack[r - 1]] >= height[i]) {
                cur = stack[--r];
                left = r == 0 ? -1 : stack[r - 1];
                ans = Math.max(ans, height[cur] * (i - left - 1));
            }
            stack[r++] = i;
        }
        while (r > 0) {
            cur = stack[--r];
            left = r == 0 ? -1 : stack[r - 1];
            ans = Math.max(ans, height[cur] * (n - left - 1));
        }
        return ans;
    }

}

五. 全是1的最大矩形

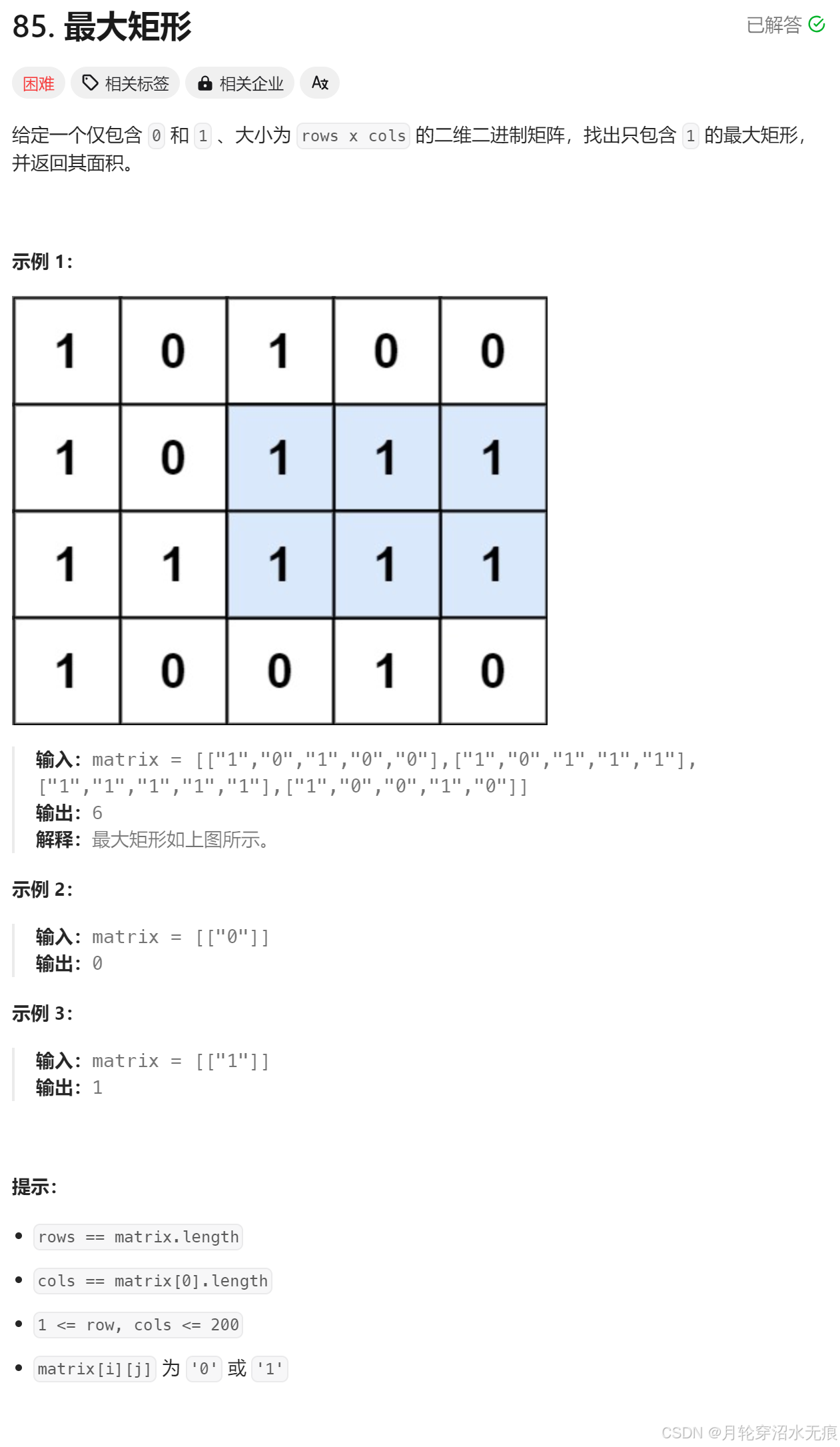
题目：最大矩形

算法原理

  • 整体思路
    • 这个算法用于解决在一个仅包含0和1的二维二进制矩阵中找出只包含1的最大矩形的问题。算法采用了一种基于高度数组和单调栈的方法，将二维问题转化为多次处理一维的最大矩形面积问题。
  • 算法步骤
    • maximalRectangle方法
      • 初始化
        • 定义了矩阵的行数为n，列数为m，并初始化高度数组height中的元素为0。同时定义变量ans用于存储最大矩形面积，初始值为0。
      • 逐行处理矩阵（外层for循环）
        • 对于每一行i：
          • 构建高度数组（内层for循环）
            • 遍历当前行的每一列j，如果当前位置grid[i][j]为0，则将高度数组height[j]设为0；如果为1，则将height[j]的值在原来基础上加1（表示以当前行为底，从第0行到当前行的连续1的高度）。
          • 计算以当前行作为底的最大矩形面积
            • 调用largestRectangleArea方法计算以当前高度数组height为基础的最大矩形面积，并将结果与ans比较，取较大值更新ans（ans = Math.max(largestRectangleArea(m), ans);）。
    • largestRectangleArea方法
      • 初始化
        • 定义栈顶指针r为0，变量ans用于存储最大矩形面积（初始值为0），以及用于临时存储栈顶元素索引的cur和栈顶元素左边索引的left。
      • 遍历高度数组（外层for循环）
        • 对于高度数组中的每个元素height[i]：
          • 处理单调栈（内层while循环）
            • 当栈不为空（r > 0）且栈顶元素对应的高度height[stack[r - 1]]大于等于height[i]时：
              • 弹出栈顶元素，将其索引存储为cur（cur = stack[--r];）。
              • 确定cur左边的索引left，如果r == 0，则left = -1，否则left = stack[r - 1];。
              • 计算以height[cur]为高的矩形面积，宽度为i - left - 1（ans = Math.max(ans, height[cur] * (i - left - 1));）。
          • 将当前索引i压入栈（stack[r++] = i;）
            • 无论是否弹出了栈顶元素，都将当前索引i压入栈中，以保持单调栈的性质。
      • 处理栈中剩余元素（外层while循环之后的while循环）
        • 当遍历完整个高度数组后，栈中可能还剩余一些元素。对于每个剩余元素cur（从栈顶开始依次处理）：
          • 确定cur左边的索引left，计算以height[cur]为高的矩形面积，宽度为m - left - 1（ans = Math.max(ans, height[cur] * (m - left - 1));）。
      • 最终结果
        • 最后返回ans，这个值就是以当前高度数组为基础的最大矩形面积。

代码实现

import java.util.Arrays;

// 最大矩形
// 给定一个仅包含 0 和 1 、大小为 rows * cols 的二维二进制矩阵
// 找出只包含 1 的最大矩形，并返回其面积
// 测试链接：https://leetcode.cn/problems/maximal-rectangle/
public class Code05_MaximalRectangle {

    public static int MAXN = 201;

    public static int[] height = new int[MAXN];

    public static int[] stack = new int[MAXN];

    public static int r;

    public static int maximalRectangle(char[][] grid) {
        int n = grid.length;
        int m = grid[0].length;
        Arrays.fill(height, 0, m, 0);
        int ans = 0;
        for (int i = 0; i < n; i++) {
            // 来到i行，长方形一定要以i行做底！
            // 加工高度数组(压缩数组)
            for (int j = 0; j < m; j++) {
                height[j] = grid[i][j] == '0' ? 0 : height[j] + 1;
            }
            ans = Math.max(largestRectangleArea(m), ans);
        }
        return ans;
    }

    public static int largestRectangleArea(int m) {
        r = 0;
        int ans = 0, cur, left;
        for (int i = 0; i < m; i++) {
            // i -> arr[i]
            while (r > 0 && height[stack[r - 1]] >= height[i]) {
                cur = stack[--r];
                left = r == 0 ? -1 : stack[r - 1];
                ans = Math.max(ans, height[cur] * (i - left - 1));
            }
            stack[r++] = i;
        }
        while (r > 0) {
            cur = stack[--r];
            left = r == 0 ? -1 : stack[r - 1];
            ans = Math.max(ans, height[cur] * (m - left - 1));
        }
        return ans;
    }

}

六.总结

单调栈最经典的用法是解决如下问题：

每个位置都求：

1）当前位置的左侧比当前位置的数字小，且距离最近的位置在哪

2）当前位置的右侧比当前位置的数字小，且距离最近的位置在哪

或者

每个位置都求：

1）当前位置的左侧比当前位置的数字大，且距离最近的位置在哪

2）当前位置的右侧比当前位置的数字小，且距离最近的位置在哪

用单调栈的方式可以做到：求解过程中，单调栈所有调整的总代价为O(n)，单次操作的均摊代价为O(1)

注意：这是单调栈最经典的用法，可以解决很多题目，下篇文章将继续介绍其他的用法

注意：单调栈可以和很多技巧交叉使用！比兔：动态规划+单调栈优化，会在【扩展】系列讲述

单调栈概念与技巧
KeePromise的博客
07-14 219
单调栈概念与技巧 总结 （1）总的来说，单调栈适合一些求解过程或者求解出的结果明显的呈现出V或者形式的问题，这种类型的问题可以考虑使用单调栈。**（可以考虑是指，按照这个特点使用单调栈不一定能绝对完成任务），**总之能用单调栈解决的问题一定符合v,，但是符合v,^形式的问题，不一定能用单调栈，的具体问题具体分析（但是大部分都可以）。 （2）求数组中一个元素的两端最近的大于或者小于该元素的元素（即左边最近的小于/大于它的元素，右边最近的小于/大于它的元素），可以求两端，当然只求一端也可以完成。——适用于第一种
LeetCode-【单调栈】解题技巧
lanzh_
10-03 246
402. 移掉 K 位数字 正常算法思路：从左到右，找第一个比后面大的字符，删除，去掉前导清零，需要k次扫描，每扫描一次，得到移除一个数字后的解。 贪心+k次扫描： class Solution: def removeKdigits(self, num: str, k: int) -> str: if len(num) == k: return "0" for i in range(k): t = ""
LeetCode单调栈总结
weixin_43510267的博客
06-13 241
1.LeetCode496.下一个更大元素Ⅰ 这里我们需要找到右边第一大的元素，此时如果从左往右遍历每个数，维护一个数据结构时，每个元素相当于存在此数据结构里，等着右边大的数来找到它，而当右边大的数比栈顶元素大的时候，说明这个栈顶元素已经找到了右边第一个比它大的元素，那就将它pop掉，然后当前元素继续和栈顶元素比较直到空栈或者栈顶元素比其大的时候，然后再将这个元素放入栈中，等着右边的元素继续来找。 整个操作其实是在维护一个从栈底到栈顶递减的栈。 int n = nums1.size();
单调栈总结
新熊君的博客
04-11 2万+
单调栈总结目录 定义 性质 功能 例题 HDU 1506 HDU 5033 PKU 2796 PKU 3250 定义性质下面引自百度百科 单调递增或单调减的栈，跟单调队列差不多，但是只用到它的一端，利用它可以用来解决一些ACM/ICPC和OI的题目，如RQNOJ 的诺诺的队列等。 单调栈是一种特殊的栈，特殊之处在于栈内的元素都保持一个单调性。 假设下图是一个栈内元素的排列情况(单调递增的
2020最新-精选基础算法100题（面试必备）
热门推荐
ATFWUS的博客
05-18 30万+
0x01.概述 作为一个程序员，算法能力必不可少，虽然不一定是算法工程师，但是算法还是彰显着个人的编码能力，面试中也经常会被问到，甚至会被要求临场做算法题，所以，还是好好积累吧。 个人其实对算法挺有兴趣的，从3月份开始，陆陆续续刷了一些算法题，把一些有意义的记录下来了，也顺便写了一些题解，个人认为，还是挺有收获的。 之前写了一篇算法文章的目录，不过后来就忘了实时去更新了，于是现在，想把之前做过的一些有意义的算法题分享出来，刚好整理了100篇比较有意义的。希望对大家有所帮助。 0x02.说明 关
面试框架题整理
Jenius87v5的博客
04-15 2万+
面试题总结 一基础部分 1.1 集合 1.1.1 fail-fast 与 fail-safe 机制有什么区别 1.1.2 说出ArrayList,Vector, LinkedList的存储性能和特性 ArrayList 采用的是数组形式来保存对象的，这种方式将对象放在连续的位置中，所以最大的缺点就是插入删除时非常麻烦 LinkedList 采用的将对象存放在独立的空间中，而且在每个空间中还保存下一个链接的索引 但是缺点就是查找非常麻烦 要丛第一个索引开始 ArrayList和Vector都是用数组方
2024最新-精选基础算法100题（面试必备）_算法题
2401_86963291的博客
09-11 971
容器类的算法题一般需要根据一些容器的特点来解决响应的问题，还有需要选择合适的容器进行新的数据结构的设计，掌握它们的使用，非常重要。树也是一种非常重要的数据结构，因为很多容器的底层都设计到树，所以树也成了面试常问的重点了，你需要对他们的一些基本算法题，非常熟练。数学思维类的题由于需要很强大的数学思维，但是这又不是一天可以练成的，所以，也常常在面试中会被问到，只有慢慢的积累，才是王道。别忽视字符串的算法问题，它难起来可以非常难，简单的也很简单，面试喜欢提问，而且特别容易出错，需要引起重视。
51c大模型~合集19
whaosoft~aiotの开发板商城
11-09 4960
GALA3D 的整体架构如下图所示：GALA3D 利用大型语言模型（LLMs）生成初始布局，并提出布局引导的生成式 3D 高斯表示构建复杂 3D 场景。GALA3D 设计通过自适应几何控制优化 3D 高斯的形状和分布，以生成具有一致几何、纹理、比例和精确交互的 3D 场景。此外，GALA3D 还提出了一种组合优化机制，结合条件扩散先验和文生图模型，协作生成具有一致风格的 3D 多物体场景，同时迭代优化从 LLMs 提取的初始布局先验，以获得更加逼真准确的真实场景空间布局。
算法数据结构必备篇章3
2301_81486828的博客
08-11 513
文章目录47. (必备)一维差分与等差数列差分48. (必备)二维前缀和, 二维差分, 离散化技巧49. (必备)滑动窗口技巧以及相关题目50. (必备)双指针技巧及相关题目51. (必备)二分答案法及相关题目52. (必备)单调栈上53. (必备)单调栈下54. (必备)单调队列上55. (必备)单调队列下56. (必备)并查集上57. (必备)并查集下 47. (必备)一维差分与等差数列差分 package class047; // 航班预订统计 // 这里有 n 个航班，它们分别从 1 到 n 进行
OTA升级AI模型：安全可靠远程更新ESP32端侧推理模型的3种实现方式（必备技能）
![OTA升级AI模型：安全可靠远程更新ESP32端侧推理模型的3种实现方式（必备技能）]...# 1. OTA升级AI模型的核心概念与技术背景 随着边缘智能设备的普及，如何在不中断服务的前提下动态更新AI模型成为关键挑战。...
LeetCode 100道题目和答案（面试必备）（二）
qq_15557237的博客
08-10 1600
我个人的理解是：「回溯算法」强调了「深度优先遍历」思想的用途，用一个 不断变化 的变量，在尝试各种可能的过程中，搜索需要的结果。在分步解决问题的过程中，当它通过尝试发现现有的分步答案不能得到有效的正确的解答的时候，它将取消上一步甚至是上几步的计算，再通过其它的可能的分步解答再次尝试寻找问题的答案。我刚开始学习「回溯算法」的时候觉得很抽象，一直不能理解为什么递归之后需要做和递归之前相同的逆向操作，在做了很多相关的问题以后，我发现其实「回溯算法」与「 深度优先遍历 」有着千丝万缕的联系。
BAT 大厂Java 面试题集锦之核心篇附参考答案
AI天才研究院
11-05 1万+
核心篇数据结构与算法网路:TCP/IP,HTTP操作系统, 文件, shell, CPU, IO, epoll, 非阻塞IO,进程/线程/协程,锁HashMap, Co...
高延迟问题逐层拆解：从RTSP协议到WebSocket链路的8层排查法（工程师必备）
[高延迟问题逐层拆解：从RTSP协议到WebSocket链路的8层排查法（工程师必备）](https://arthurchiao.art/assets/img/tcp-retransmission-may-be-misleading/retrans-types-and-scope.png) # 摘要 高延迟问题是影响...
剑指Offer66道题和答案（Java完整版 面试必备）
lx_lollipop的博客
03-18 4539
最近忙着准备春招，复习完这个又复习那个。不过还是忙里偷闲，把剑指Offer这66道题目重新刷了一遍，收获还是很大的，下面贴出答案，又不懂的可以给我留言，博主会及时解答。 我的github 准备把春招复习的知识都整理到github上，一边是自己做个总结，一边也能供大家参考 附——leetcode数据库19道题 以下摘自牛客网剑指Offer 1.二维数组中的查找 2.替换空格 3.从尾到头打印链表 ...
数据结构：二叉树
闲余知道
12-04 425
数据结构：二叉树
数据结构：红黑树
闲余知道
12-04 1307
数据结构：红黑树
数据结构：平衡二叉树
闲余知道
12-04 373
数据结构：平衡二叉树
嵌入式第二十六篇——数据结构双向链表
2303_78799336的博客
12-02 611
摘要：本文介绍了双向链表的基本概念和C语言实现。双向链表的每个节点包含指向前驱和后继节点的指针，支持双向遍历。文章详细说明了节点定义、链表创建方法，以及头部/尾部插入、删除节点等核心操作的具体实现。同时给出了正向和反向遍历链表的代码示例。双向链表相比单向链表具有更高的操作灵活性，适用于需要双向访问的场景。
数据结构--队列
最新发布
2301_78295956的博客
12-05 706
本文介绍了队列的基本概念、实现方式及应用场景。队列是一种先进先出（FIFO）的线性表，分为顺序队列（循环队列）和链式队列两种实现方式。顺序队列使用数组存储，通过模运算解决越界问题，需牺牲一个存储单元区分队空队满；链式队列动态扩展，无空间限制但需额外指针开销。文章对比了两种队列的特性，分析了它们在缓冲区管理、任务调度、算法实现等场景的应用，并强调了边界处理、线程安全等注意事项。两种队列的基本操作时间复杂度均为O(1)，顺序队列空间效率更高，链式队列灵活性更强。
Keil与Proteus联调必备的vdm51.dll文件使用指南
标题所涉及的知识点是关于在Keil和Proteus软件中进行联合调试时必备的vdm51.dll文件。描述中简短地强调了该文件的重要性，而标签部分则提示了本文要探讨的内容范围。以下将详细介绍这些知识点： ### 什么是Keil软件...
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值