计算智能——聚类算法之k-means算法

聚类算法之k-means算法

基本思想：

它是基于给定的聚类目标函数，算法采用迭代更新的方法，每一次迭代过程都是向目标函数减小的方向进行，最终聚类结果使得目标函数取得极小值，达到较好的分类效果。

算法原理

在k-means的损失函数中存在两个未知的参数：一个是每个数据所属的类别{ti}；一个是每个聚类的中心{μi}。这两个未知的参数是相互依存的：如果知道每个数据的所属类别，那么类别的所有数据的平均值就是这个类别的中心；如果知道每个类别的中心，那么就是计算数据与中心的距离，再根据距离的大小可以推断出数据属于哪一个类别。
针对每个点，计算这个点距离所有中心点最近的那个中心点，然后将这个点归为这个中心点代表的簇。一次迭代结束之后，针对每个簇类，重新计算中心点，然后针对每个点，重新寻找距离自己最近的中心点。如此循环，直到前后两次迭代的簇类没有变化。

算法步骤

1. 首先随机生成k个聚类中心点
2. 根据聚类中心点，将数据分为k类。分类的原则是数据离哪个中心点近就将它分为哪一类别。
3. 再根据分好的类别的数据，重新计算聚类的类别中心点。
4. 不断的重复2和3步，直到中心点不再变化。

流程图

Kmeans 对“亲疏程度”的测度

通常，“亲疏程度”的测度一般都有两个角度：第一，数据间的相似程度；第二，数据间的差异程度。衡量相似程度一般可采用简单相关系数或等级相关系数等，差异程度则一般通过某种距离来测度。Kmeans聚类方法采用的是第二个测度角度。

为有效测度数据之间的差异程度， Kmeans聚类算法将所收集到具有p个变量的样本数据，看成p维空间上的点，并以此定义某种距离。通常，点与点之间的距离越小，意味着它们越“亲密”，差异程度越小，越有可能聚成一类；相反，点与点之间的距离越大，意味着它们越“疏远”，差异程度越大，越有可能分属不同的类。

由于Kmeans聚类方法所处理的聚类变量均为数值型，因此，它将点与点之间的距离定义为欧氏距离，即数据的距离是两个点的p个变量之差的平方和的算术平方根，数学定义为
d(x,y)=$\sqrt{(}x1-y1{)}^2+(x2-y2{)}^2+(x3-y3{)}^2..$

实例

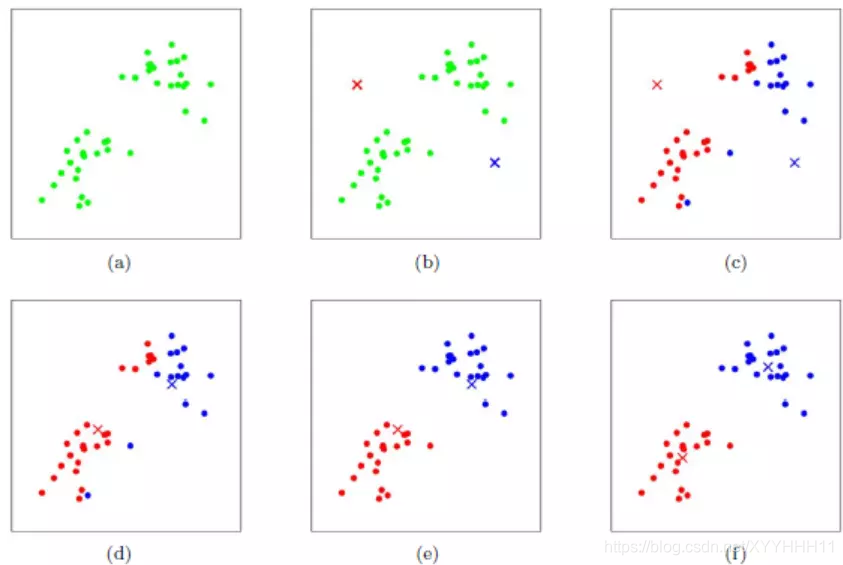
（a）带聚类样本，现将样本目标聚成2类。
（b）选取2个中心点，即k=2。
（c）对每个样本，找到距离自己最近的中心点，完成一次聚类。聚类前后样本点的聚类情况不相同，继续下一步。
（d）根据c类聚的结果更新中心点。同时，再次进行c步骤，聚类前后样本点的聚类情况不相同，继续下一步。
（e）根据d类聚的结果更新中心点。同时，再次进行c步骤，聚类前后样本点的聚类情况不相同，继续下一步。
（e）聚类前后样本点的聚类情况不相同，算法结束。

优缺点

优点
1、原理比较简单，实现也是很容易，收敛速度快。
2、当结果簇是密集的，而簇与簇之间区别明显时, 它的效果较好。

缺点
1、K值需要预先给定。
2、开局不同的中心点 对结果影响很大。
3、对噪音和异常点比较的敏感。
4、采用迭代方法，可