最大元(最大元素)、最小元(最小元素)
对于偏序集<A,≤>和集合A的任意子集B,如果存在元素b∈B,使得任意x∈B都有x≤b,则称b为B的最大元素(greatest element),简称为最大元;如果存在元素b∈B,使得任意x∈B都有b≤x,则称b为B的最小元素(smallest element),简称为最小元。
例:集合A={2,3,4,6,12,24,36}上整除关系:
R={<2,2>,<2,4>,<2,6>,<2,12>,<2,24>,<2,36>,
<3,3>,<3,6>,<3,12>,<3,24>,<3,36>,
<4,4>,<4,12>,<4,24>,<4,36>,
<6,6>,<6,12>,<6,24>,<6,36>,
<12,12>,<12,24>,<12,36>,
<24,24>,
<36,36>}
求={6,12},
={2,3,12},
={2,3,4,6,12,24},
={6,12,24,36}的最大元和最小元。
:<6,12>;
:2,3不可比,无最小元;
:2,3不可比,无最小元;
:24,36不可比,无最大元;
| 最大元 | 最小元 | |
| 12 | 6 | |
| 12 | 无 | |
| 24 | 无 | |
| 无 | 6 |
极大元、极小元
对于偏序集<A,≤>和集合A的任意子集B,如果存在元素b∈B,使得B中不存在其他元素x满足b≤x,则称b为B的极大元素(maximal element),简称为极大元;如果存在元素b∈B,使B中不存在其他元素x满足x≤b,则称b为B的极小元素(minimal element),简称为极小元。
求={6,12},
={2,3,12},
={2,3,4,6,12,24},
={6,12,24,36}的极大元和极小元。
| 极大元 | 极小元 | |
| 12 | 6 | |
| 12 | 2,3 | |
| 24 | 2,3 | |
| 36,24 | 6 |
上界、下界
对于偏序集<A,≤>和集合A的任意子集B,如果存在元素a∈A,使得任意x∈B都有x≤a,则称a为子集B的上界(upperbound);如果存在元素a∈A,使得任意x∈B都有a≤x,则称a为子集B的下界(lower bound)。
注意:偏序集<A,≤>的任意子集B的上(下)界不一定是集合B中的元素。
求={6,12},
={2,3,12},
={2,3,4,6,12,24},
={6,12,24,36}的上界和下界。
:<6,12>;
:2,3不可比,无下界;
:24,36不可比,36不是上界;2,3不可比,无下界;
:24,36不可比,无上界;
| 上界 | 下界 | |
| 36,24,12 | 2,3,6 | |
| 36,24,12 | 无 | |
| 24 | 无 | |
| 无 | 2,3,6 |
上确界(最小上界)、下确界(最大下界)
对于偏序集<A,≤>和集合A的任意子集B,如果存在子集B的上界a,使B的任意上界x都有a≤x,则称a为子集B的最小上界(least upper bound)或上确界,记为sup(B)=a;如果存在子集B的下界a,使B的任意下界x都有x≤a,则称a为子集B的最大下界(greatest lower bound)或下确界,记为inf(B)=a。换言之,如果C是B的所有上界的集合,则C的最小元c称为B的最小上界或上确界;如果C是B的所有下界的集合,则C的最大元c称为B的最大下界或下确界。
求={6,12},
={2,3,12},
={2,3,4,6,12,24},
={6,12,24,36}的上确界和下确界。
:上确界:min(36,24,12);下确界:max(2,3,6);
:上确界:min(36,24,12);无下确界;
:上确界:24;无下确界;
:无上确界;下确界:max(2,3,6);
| 上确界 | 下确界 | |
| 12 | 6 | |
| 12 | 无 | |
| 24 | 无 | |
| 无 | 6 |
全序关系
对于偏序集<A,≤>,如果A中任意两个元素x和y都是有关系的(或者x和y是可比的),即x≤y或者y≤x,则称该偏序关系为全序关系(total order relation),简称为全序,或者线序关系,简称为线序。并称<A,≤>为全序集(total order set),或者线序集,或者链(chain)。
良序关系
对于偏序集<A,≤>,如果A的任意一个非空子集都有最小元素,则称该偏序关系为良序关系(well order relation),简称为良序。并称<A,≤>为良序集(well order set)。
例:集合A={2,3,4,6,12,24,36}上整除关系,此偏序关系是否为全序关系或良序关系?
2,3;3,4;4,6;24,36不可比——>非全序关系或良序关系。
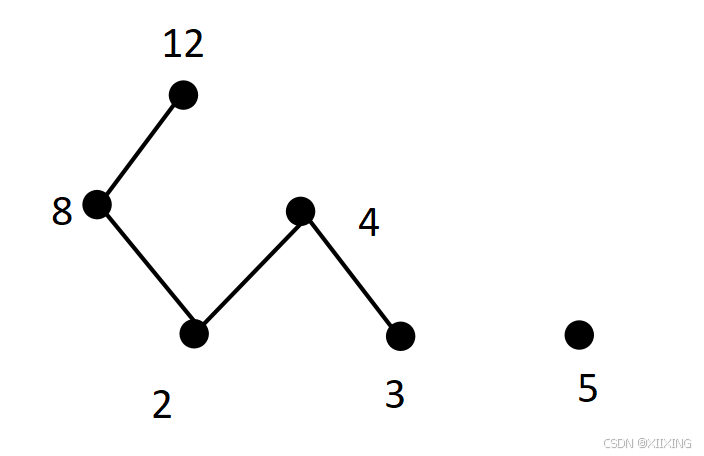
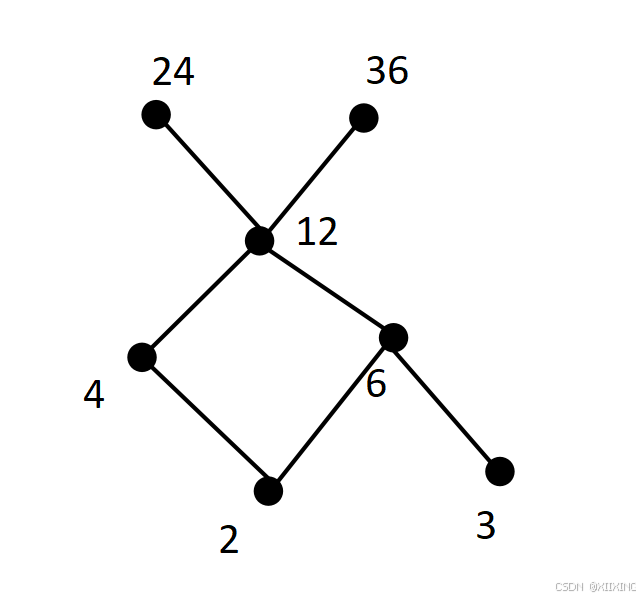
观察下列哈斯图是否为全序关系或良序关系?
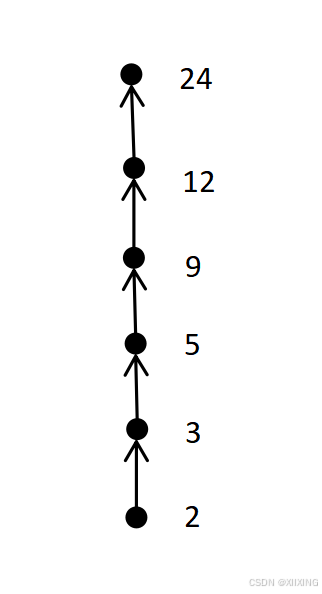
:哈斯图—>传递性,由图任意一个非空子集都有最小元素—>良序关系;任意两元素可比—>全序关系;
:存在不可比—>非全序关系或良序关系;
:存在不可比—>非全序关系或良序关系。




















 2189
2189

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








