编程内容
关于今天做作业发现,使用DEV C++对所要填写的内容进行编程时发现的return语句的问题
题目
以下函数的功能时求字符指针p指向的字符串的长度,请补充缺少的代码。
int strlength(char *p)
{
if(*p=='\0')
return 0;
return 1+____;
}
编程中出现问题(重点)
- 第一次编程的内容(有问题):
#include <iostream>
using namespace std;
int strlength(char *p);
int main(void)
{
int len;
char arr[]="welcom";
len=strlength(arr);
cout<<"字符串长度为:"<<len<<endl;
}
int strlength(char *p)
{
if(*p=='\0')
return 0;
return 1+strlength(p++);
}
结果居然是:
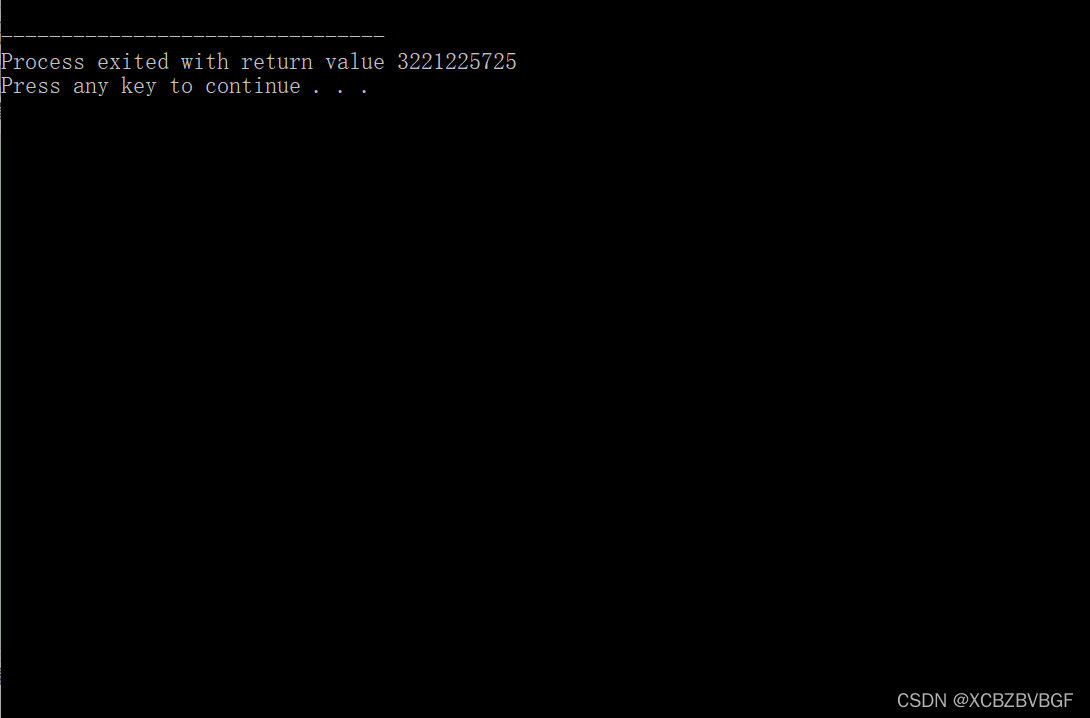
于是我便开始找原因,但我总觉得问题就出在了下面这条return语句中
return 1+strlength(p++);
果不其然,于是有了下面的编程(只摘有用的来看)
2. 第二次编程内容(正确可解):
#include <iostream>
using namespace std;
int strlength(char *p);
int main(void)
{
int len;
char arr[]="welcom";
len=strlength(arr);
cout<<"字符串长度为:"<<len<<endl;
}
int strlength(char *p)
{
if(*p=='\0')
return 0;
return 1+strlength(++p);
}
结果居然是OK的了(我是小菜鸡,若有大神造访,勿喷)
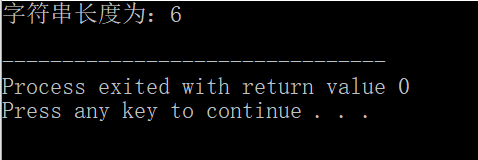
于是我就开始纳闷为什么,上网搜索了return p++是否会执行p加1的内容,可是看的眼花缭乱,于是我加了句代码看了一遍,果然,编程思维yyds。
分析原因
两种编程的比较
(1)正确的
return 1+strlength(++p);
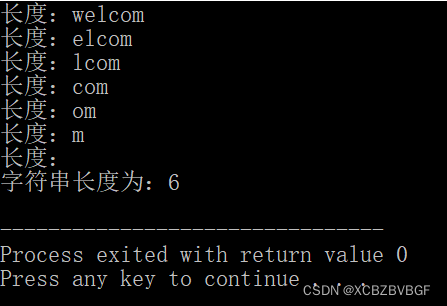
(2)错误的
return 1+strlength(p++);
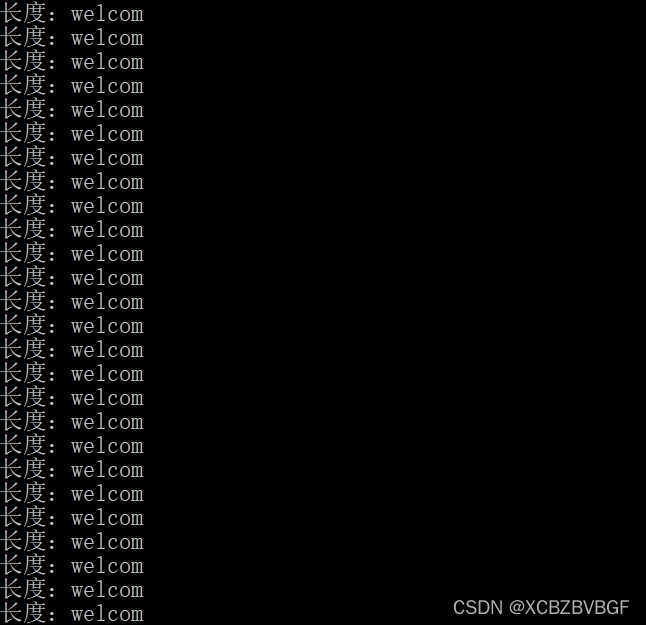
这是个没有结果的编程,一直welcom。
原因:在++p时是执行了p=p+1再返回值,而p++是执行了return但没有执行p=p+1,这样就永远跳不出strlength这个函数,所以没有输出。





 本文通过一个编程实例探讨了C++中return语句中使用p++和++p的区别。作者在编写求字符串长度的递归函数时,发现return1+strlength(p++)会导致无限循环,而return1+strlength(++p)则能得到正确结果。问题在于++p先增加指针再返回,而p++先返回再增加指针,导致前者未执行指针的更新。
本文通过一个编程实例探讨了C++中return语句中使用p++和++p的区别。作者在编写求字符串长度的递归函数时,发现return1+strlength(p++)会导致无限循环,而return1+strlength(++p)则能得到正确结果。问题在于++p先增加指针再返回,而p++先返回再增加指针,导致前者未执行指针的更新。


















 1万+
1万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










