专题5-2 分块：离线莫队算法

专题5-2 分块：离线莫队算法

PART 1 名词点击

Q1 什么是莫队算法？

这个词可就不能像专题5-1那样顾名思义了，你可一眼看不出来这是什么

我问一个班级里的化学竞赛生：“你知道莫队吗？”
他说：“莫队？不要排队？食堂要是这样就好了。”
对话结束

好吧，这个词你在百度上查也没有，倒是有很多的算法教学文章

这是个啥啊！！！

扯远了
莫队有两种形式，一个是维护区间答案，一个是维护区间数据结构
他的思想是暴力，但是借助了分块的优化

Q2 什么是离线？

OIer们的题目无外乎分为离线和在线（什么交互题的我没有听过！！ ）
在线的意思是操作必须一步一步进行，随着你的读入而输出答案

例：Luogu P1198 [JSOI2008] 最大数

而离线的意思是我先把所有输入先记录下来，之后再进行一系列操作
之后我们会解释为什么莫队需要离线

Q3 什么是分块？

请左转我的博客 专题5-1

PART 2 离线莫队算法

首先我们来考虑一下一个经典问题

Q 对于一个序列，包含k种颜色，求所有对于[ l , r ]的区间中有多少不同颜色

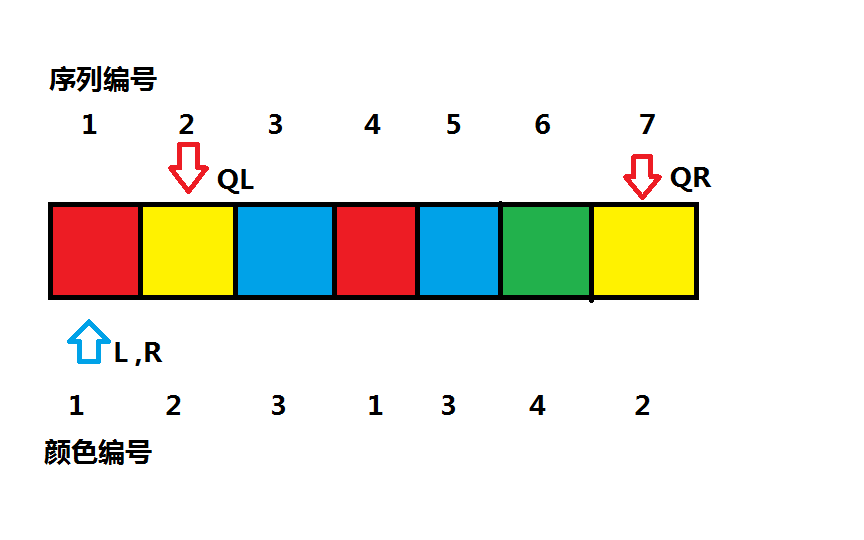
设ans [ i ] 为 [ ql , qr ] 区间出现的颜色个数
（举例，当ql = 3 , qr = 6 时，ans [ 1 ] = 1,ans [ 2 ] = 1,ans [ 3 ] = 2 ,ans [ 4 ] = 1）

我们当前有 l = 1 , r = 1
则此时有ans [ 1 ] = 1,其余均为0

我们考虑当 r 移动时 ans [ i ] 的变化情况
假如我们把 r 移动到2时 我们有 ans[ 2 ] ++

以此类推
当 r 移动到7（==qr）时，有
ans [ 1 ] = 2,ans [ 2 ] = 2,ans [ 3 ] = 2 ,ans [ 4 ] = 1

当 l 移动到2（==ql）时，有
ans [ 1 ] = 1,ans [ 2 ] = 2,ans [ 3 ] = 2 ,ans [ 4 ] = 1

我们怎么统计答案数量？
这个操作要在 r 和 l 转移时进行
当我们对ans数组操作时，如果ans [ 修改 ] 在增加时变为了1，则将tot++
如果在减少时变为了0，则将tot- -

以下是关键代码

while(r<qr)
{
	++r;++ans[r];if(ans[r]==1)++tot;
}
while(l<ql)
{
	--ans[l];++l;if(ans[l]==0)--tot;
}
while(r>qr)
{
	--ans[r];--r;if(ans[r]==0)--tot;
}
while(l>ql)
{
	--l;++ans[l];if(ans[l]==1)++tot;
}

请尤其在意 l 和 r 自增自减和 ans 变化的先后顺序

可是如果这样的话，我们每次移动都需要O（1）的时间复杂度
总的来说时间复杂度还是O（询问次数*区间长度）

怎么优化呢？

将左端点为第一关键字，将右端点为第二关键字排序？看似可以满足要求

实则不然，因为我们的 l 和 r 都是一个一个移动的，这样会导致当我们的 l 移动时会导致 r 的大幅度移动，依旧很浪费时间

我们可以结合分块来排序，如果左端点在一个块中，就对右端点排序

for(int i=1;i<=n;i++)belong[i]=(i-1)/base+1;//分块操作，base=sqrt(n)

bool cmp(const q &a,const q &b)// q 代表我们记录颜色的数组
{
    if(bl[a.x]==bl[b.x]) return a.y<b.y;
    else return a.r<b.r;
}

PART 3 玄学优化

3.1 奇偶排序优化

不知道是谁搞出的这种优化，看起来没什么用处，实则能帮你加快不少
（大概每个点200ms？）

原理是对于左端点在一个奇数块内的询问，右端点按升序排列
在一个偶数块内的询问，右端点按降序排列

即将

for(int i=1;i<=n;i++)belong[i]=(i-1)/base+1;//分块操作，base=sqrt(n)

bool cmp(const q &a,const q &b)// q 代表我们记录颜色的数组
{
    if(bl[a.x]==bl[b.x]) return a.y<b.y;
    else return a.r<b.r;
}

改为

bool cmp(const q &a,const q &b) 
{
    return(belong[a.x]^belong[b.x])?belong[a.x]<belong[b.x]:((belong[a.x]&1)?a.y<b.y:a.y>b.y);
}

（我也不知道这个优化是什么东西，反正优化的很爽就行了）
Updated in 2019/3/29
我大概了解这个优化是什么东西了
一开始时，你会先处理询问左端点在第一个块内的询问。

这样的话，你的 r 会从第一个块跑到将近最后的位置，如果你要处理第二个块的询问，你的 r 就会从最后跑到最前，这样的话，你每处理一个块，你的 r 就会移动 2n 次

如果优化后，你的 r 在回来的时候就能处理偶数块内的询问，这样的话，你每处理两个块，你的 r 就会移动 2n 次，这样的话，你的效率会大大提升。

3.2 三目运算符的优化

我们都知道，莫队算法的 l 和 r 指针移动的时间复杂度为O（1）

而这个操作要进行很多次，如果你的时间复杂度大于O（1），那你的效率要大大降低

反之，如果你的时间复杂度小于O（1），你的效率会大大提升

我们就从这里入手，利用三目运算符加快普通的修改

即将

while(r<qr)
{
	++r;++ans[r];if(ans[r]==1)++tot;
}
while(l<ql)
{
	--ans[l];++l;if(ans[l]==0)--tot;
}
while(r>qr)
{
	--ans[r];--r;if(ans[r]==0)--tot;
}
while(l>ql)
{
	--l;++ans[l];if(ans[l]==1)++tot;
}

改为

while(l<ql)tot-=!--ans[v[l++]];
while(l>ql)tot+=!ans[v[--l]]++;
while(r<qr)tot+=!ans[v[++r]]++;
while(r>qr)tot-=!--ans[v[r--]];

这样，你的程序又能加快200ms

3.3 手写快读

不用说了，OIer日常专用加速方法

PART 4 例题

1.Luogu P3901 数列找不同
2.Luogu P2709 小B的询问
提示：(n+1)²-n²=2n
3.Luogu P1494 [2009国家集训队]小Z的袜子
提示：请注意总的方案数与可行方案总数的关系（组合数）
4.你终于可以把这个毒瘤题A了 数列分块9
5.Luogu P1972 [SDOI2009]HH的项链
提示：本题少许卡莫队，请尝试玄学优化