代码随想录--3.哈希表学习记录

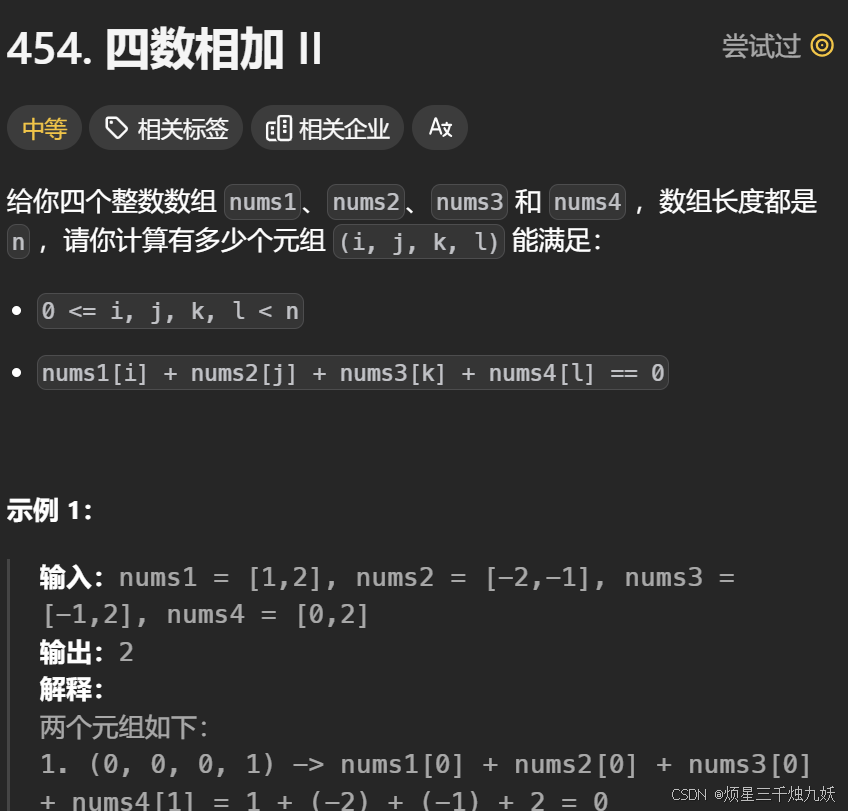
四数相加

我两重for循环全连接合并俩数组怎么你了，最长才200长度的n，组合一下也不过4000，时间复杂度O(n2logn)，测试用例这都顶不住，dying！

class Solution {
public:
    int fourSumCount(vector<int>& nums1, vector<int>& nums2, vector<int>& nums3, vector<int>& nums4) {
        //unordered_set<vector<int>> solo;
        multiset<int> solo;
        multiset<int> sol;
        int x=0;
        int n=nums1.size();
        for(int i=0;i<n;i++){
            for(int j=0;j<n;j++){
                solo.insert(nums1[i]+nums2[j]);
            }
        }
        for(int i=0;i<n;i++){
            for(int j=0;j<n;j++){
                sol.insert(nums3[i]+nums4[j]);
            }
        }
        for(const auto& so:solo){
            x+=sol.count(0-so);
        }
        return x;
    }
};

掉眼泪了，看了解析发现问题，multiset的查询效率是logn，本来当时写的时候就在考虑用map还是set，后来想想只要组合之后两数相加，跟键值对有毛关系，果断选set。

然后因为可能有很多重复是允许的，所以选了红黑树打底的multiset，不然我选unorder_set肯定就完事儿了，可惜不能重复元素，哎。

所以科学来说，为了效率应该用unordered_map，啊啊啊啊啊啊！

class Solution {
public:
    int fourSumCount(vector<int>& nums1, vector<int>& nums2, vector<int>& nums3, vector<int>& nums4) {
        //unordered_set<vector<int>> solo;
        unordered_map<int,int> solo;
        unordered_map<int,int> sol;
        int x=0;
        int n=nums1.size();
        for(auto a:nums1){
            for(auto b:nums2){
                solo[a+b]++;
            }
        }
        for(auto a:nums3){
            for(auto b:nums4){
                sol[a+b]++;
            }
        }
        for(const auto& so:solo){
            auto it=sol.find(0-so.first);
            if(it!=sol.end())
            x+=(it->second)*(so.second);
            else continue;
        }
        
        return x;
    }
};

改成这样就可以了，哎，顺便换了好看点的循环，我恨。

三数之和

哈哈哈哈哈自己写出来的，在刷hot100的时候还没复习到哈希这边，当时花了点功夫debug，主要思路就是双指针，先排个序，这样第二个跟第三个是互相制约的，等于他俩共用一个n的时间复杂度。第一个数慢慢挪不着急，剩下俩双向奔赴。

class Solution {
public:
    vector<vector<int>> threeSum(vector<int>& nums) {
        sort(nums.begin(),nums.end());
        int n=nums.size();
        vector<vector<int>> hey;
        for(int i=0;i<n-2;i++){
            if(i>0 && nums[i]==nums[i-1]) continue;
            int k=n-1;
            int x=nums[i];
            for(int j=i+1;j<n-1;j++){    
                if(j>i+1 && nums[j]==nums[j-1]) continue;          
                int z=0-x-nums[j];
                while(j<k && nums[k]>z) k--;
                if(j==k) break;
                z=0-x-nums[j];
                if(nums[k]==z){                   
                    hey.push_back({x,nums[j],z});
                    continue;
                }              
            }
        }
        return hey;
    }
};

哎，看的赏心悦目。就是写的时候一些小边界条件需要注意，比较容易出问题。

四数之和

这个是出生，不想说什么了，代码里全都有，继承自三数之和

class Solution {
public:
    vector<vector<int>> fourSum(vector<int>& nums, int target) {
        //unordered_set<>
        vector<vector<int>> solo;
        sort(nums.begin(),nums.end());
        int n=nums.size();
        long tar=target;//出生
        for(int i=0;i<n-3;i++){
            if(i>0&&nums[i]==nums[i-1])continue;
            for(int j=i+1;j<n-2;j++){
                if(j>i+1&&nums[j]==nums[j-1])continue;
                long goa=tar-nums[i]-nums[j];
                for(int k=j+1,m=n-1;k<n-1;k++){
                    if(k>j+1&&nums[k]==nums[k-1])continue;
                    while(k<m&& (nums[k]+nums[m])>goa)m--;//＞号才有机会匹配，不信改成!=试试
                    if(k==m) break;
                    if(nums[k]+nums[m]==goa){
                        solo.push_back({nums[i],nums[j],nums[k],nums[m]});
                        continue;
                    }                
                }

            }
        }
        return solo;
    }
};