一、简介
首先,主题模型(topic model)是以非监督学习的方式对文集的隐含语义结构(latent semantic structure)进行聚类(clustering)的统计模型。
隐含狄利克雷分布(Latent Dirichlet Allocation,LDA) 模型是一种常见的主题模型,在主题模型中占有非常重要的地位,常用来文本分类。LDA由Blei, David M.、Ng, Andrew Y.、Jordan于2003年提出,用来推测文档的主题分布。它可以将文档集中每篇文档的主题以概率分布的形式给出,从而通过分析一些文档抽取出它们的主题分布后,便可以根据主题分布进行主题聚类或文本分类。
二、文本建模
由于我们要研究的是文档的主题,所欲先看看文本的建模方法。对于一篇文档,可以看成是一组有序的词的序列 d = ( w 1 , w 2 , . . . , w n ) d=(w_1,w_2,...,w_n) d=(w1,w2,...,wn) . 从统计学角度来看,文档的生成可以看成是上帝抛掷骰子生成的结果,每一次抛掷骰子都生成一个词汇,抛掷N次生成一篇文档。在统计文本建模中,我们希望猜测出上帝是如何玩这个游戏的,这会涉及到两个最核心的问题:
- 上帝都有什么样的骰子;
- 上帝是如何抛掷这些骰子的;
第一个问题就是表示模型中都有哪些参数,骰子的每一个面的概率都对应于模型中的参数;第二个问题就表示游戏规则是什么,上帝可能有各种不同类型的骰子,上帝可以按照一定的规则抛掷这些骰子从而产生词序列。
三、Unigram Model
对于文本建模,第一种模型是Unigram Model,在Unigram Model中,我们采用词袋模型,假设了文档之间相互独立,文档中的词汇之间相互独立。假设我们的词典中一共有 V 个词 v 1 , v 2 , . . . , v V v_1,v_2,...,v_V v1,v2,...,vV,那么最简单的 Unigram Model 就是认为上帝是按照如下的游戏规则产生文本的:
(1) 上帝只有一个骰子,这个骰子有V面,每个面对应一个词,各个面的概率不一;
(2) 每抛掷一次骰子,抛出的面就对应的产生一个词;如果一篇文档中N个词,就独立的抛掷n次骰子产生n个词;
所谓词袋模型,是将一篇文档,我们仅考虑一个词汇是否出现,而不考虑其出现的顺序。在词袋模型中,“我喜欢你”和“你喜欢我”是等价的。与词袋模型相反的一个模型是n-gram,n-gram考虑了词汇出现的先后顺序。
3.1 频率派视角
对于一个骰子,记各个面的概率为 p ⃗ = ( p 1 , p 2 , . . . , p V ) \vec p=(p_1,p_2,...,p_V) p=(p1,p2,...,pV), 每生成一个词汇都可以看做一次多项式分布,记为 w ∼ M u l t i ( w ∣ p ⃗ ) w \sim Multi(w|\vec p) w∼Multi(w∣p) 。一篇文档 d = w ⃗ = ( w 1 , w 2 , . . . , w n ) d=\vec w=(w_1,w_2,...,w_n) d=w=(w1,w2,...,wn), 其生成概率是 p ( w ⃗ ) = p ( w 1 , w 2 , . . . , w n ) = p ( w 1 ) p ( w 2 ) . . . p ( w n ) p(\vec w)=p(w_1,w_2,...,w_n)=p(w_1)p(w_2)...p(w_n) p(w)=p(w1,w2,...,wn)=p(w1)p(w2)...p(wn)
文档之间,我们认为是独立的,对于一个语料库(包含多个文档),产生的该语料库可以表示为:
W
=
(
w
⃗
1
,
w
⃗
2
,
.
.
.
,
w
⃗
n
)
W=(\vec w_1,\vec w_2,...,\vec w_n)
W=(w1,w2,...,wn)
假设语料中总的词频是N,记每个词
w
i
w_i
wi 的频率为
n
i
n_i
ni, 那么
n
⃗
=
(
n
1
,
n
2
,
.
.
.
,
n
V
)
\vec n=(n_1,n_2,...,n_V)
n=(n1,n2,...,nV) , 服从多项式分布:
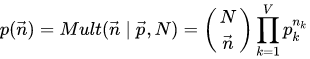
整个语料库的概率为:
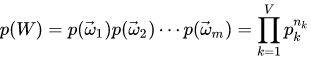
此时,我们需要估计模型中的参数
p
⃗
\vec p
p ,也就是词汇骰子中每个面的概率是多大,按照频率派的观点,使用极大似然估计最大化
p
(
W
)
p(W)
p(W), 于是参数
p
i
p_i
pi 的估计值为:
p
^
=
n
i
N
\hat p=\frac{n_i}{N}
p^=Nni,也就是词频/总的词频。
3.2 贝叶斯派视角
对于以上模型,贝叶斯统计学派的统计学家会有不同意见,他们会很挑剔的批评只假设上帝拥有唯一一个固定的骰子是不合理的。在贝叶斯学派看来,一切参数都是随机变量,以上模型中的骰子 p ⃗ \vec p p 不是唯一固定的,它也是一个随机变量。所以按照贝叶斯学派的观点,上帝是按照以下的过程在玩游戏的:
(1) 现有一个装有无穷多个骰子的坛子,里面装有各式各样的骰子,每个骰子有V个面;
(2) 现从坛子中抽取一个骰子出来,然后使用这个骰子不断抛掷,直到产生语料库中的所有词汇。
坛子中的骰子无限多,有些类型的骰子数量多,有些少。从概率分布角度看,坛子里面的骰子
p
⃗
\vec p
p 服从一个概率分布
p
(
p
⃗
)
p(\vec p)
p(p) , 这个分布称为参数
p
⃗
\vec p
p 的先验分布。在此视角下,我们并不知道到底用了哪个骰子,每个骰子都可能被使用,其概率由先验分布来决定。对每个具体的骰子,由该骰子产生语料库的概率为
p
(
W
∣
p
⃗
)
p(W|\vec p)
p(W∣p) , 故产生语料库的概率就是对每一个骰子上产生语料库进行积分求和:
p
(
W
)
=
∫
p
(
W
∣
p
⃗
)
p
(
p
⃗
)
d
p
⃗
p(W)=\int p(W|\vec p)p(\vec p)d \vec p
p(W)=∫p(W∣p)p(p)dp
先验概率有很多选择,但我们注意到
p
(
n
⃗
)
=
M
u
l
t
i
(
n
⃗
∣
p
⃗
,
N
)
p(\vec n)=Multi(\vec n|\vec p,N)
p(n)=Multi(n∣p,N)。 我们知道多项式分布和狄利克雷分布是共轭分布,因此一个比较好的选择是采用狄利克雷分布:
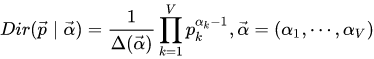
此处
Δ
(
α
⃗
)
\Delta(\vec \alpha)
Δ(α),就是归一化因子
D
i
r
(
α
⃗
)
Dir(\vec \alpha)
Dir(α) , 即:
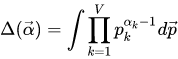
由多项式分布和狄利克雷分布是共轭分布,可得:
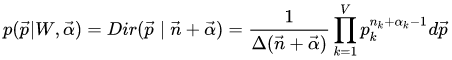
此时,我们如何估计参数
p
⃗
\vec p
p 呢?根据上式,我们已经知道了其后验分布,所以合理的方式是使用后验分布的极大值点,或者是参数在后验分布下的平均值。这里,我们取平均值作为参数的估计值。根据Dirichlet分布中的内容,可以得到:
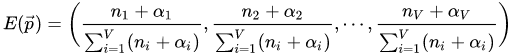
对于每一个
p
i
p_i
pi , 我们使用下面的式子进行估计:
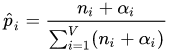
α
i
\alpha_i
αi 在 Dirichlet 分布中的物理意义是事件的先验的伪计数,上式表达的是:每个参数的估计值是其对应事件的先验的伪计数和数据中的计数的和在整体计数中的比例。由此,我们可以计算出产生语料库的概率为:
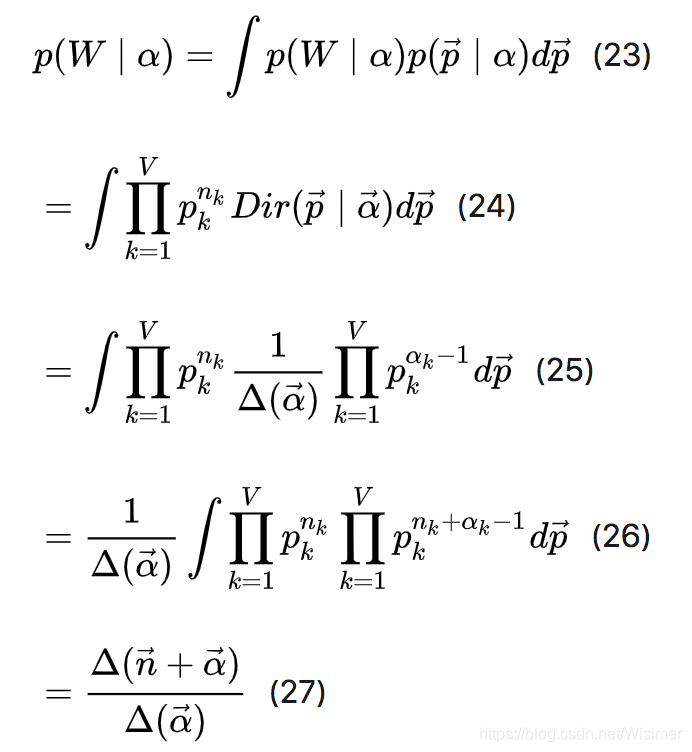
四、pLSA(Probabilistic latent semantic analysis,概率隐性语义分析)模型
Unigram Model模型中,没有考虑主题词这个概念。我们人写文章时,写的文章都是关于某一个主题的,不是满天胡乱的写,比如一个财经记者写一篇报道,那么这篇文章大部分都是关于财经主题的,当然,也有很少一部分词汇会涉及到其他主题。所以,PLSA认为生成一篇文档的生成过程如下:
(1) 现有两种类型的骰子,一种是doc-topic骰子,每个doc-topic骰子有K个面,每个面一个topic的编号;
一种是topic-word骰子,每个topic-word骰子有V个面,每个面对应一个词;
(2) 现有K个topic-word骰子,每个骰子有一个编号,编号从1到K;
(3) 生成每篇文档之前,先为这篇文章制造一个特定的doc-topic骰子,重复如下过程生成文档中的词:
(3.1) 投掷这个doc-topic骰子,得到一个topic编号z;
(3.2) 从K个topic-word骰子中选择编号为z的那个,投掷这个骰子,得到一个词;
总结一下就是:
- 按照概率 p ( d i ) p(d_i) p(di) 选择一篇文档 d i d_i di;
- 根据选择的文档 d i d_i di,从从主题分布中按照概率 p ( ζ k ∣ d i ) p(\zeta_k|d_i) p(ζk∣di) 选择一个隐含的主题类别 ζ k \zeta_k ζk,( ζ : z e t a \zeta:zeta ζ:zeta);
- 根据选择的主题 ζ k \zeta_k ζk, 从词分布中按照概率 p ( w j ∣ ζ k ) p(w_j|\zeta_k) p(wj∣ζk) 选择一个词 w j w_j wj。
可以用下图表示pLSA模型生成文档的过程:

五、LDA模型
用一句通俗的话讲:LDA 就是 PLSA 的贝叶斯化版本。LDA 在 PLSA 的基础上,为主题分布和词分布分别加了两个 Dirichlet 先验。
LDA 中,生成文档的过程如下:
- 按照先验概率 p ( d i ) p(d_i) p(di) 选择一篇文档 d i d_i di;
- 从Dirichlet分布 α \alpha α 中取样生成文档 d i d_i di 的主题分布 θ i \theta_i θi,主题分布 θ i \theta_i θi 由超参数为 α \alpha α 的Dirichlet分布生成;
- 从主题的多项式分布 θ i \theta_i θi 中取样生成文档 d i d_i di 第 j 个词的主题 z i , j z_{i,j} zi,j;
- 从Dirichlet分布 β \beta β 中取样生成主题 z i , j z_{i,j} zi,j 对应的词语分布 ; ϕ z i , j \phi_{z_{i,j}} ϕzi,j,词语分布 ϕ z i , j \phi_{z_{i,j}} ϕzi,j 由参数为 β \beta β 的Dirichlet分布生成;
- 从词语的多项式分布 ϕ z i , j \phi_{z_{i,j}} ϕzi,j中采样最终生成词语 w i , j w_{i,j} wi,j。
LDA是一种三层的贝叶斯模型:
- 第一层贝叶斯就是先从第一个超参 α \alpha α(先验分布参数)得到一个主题分布 θ \theta θ(文章属于主题的贝叶斯)。
- 然后第二层是对于每个主题的词语分布 ϕ \phi ϕ,它也有一个先验分布参数 β \beta β,从 β \beta β 到 ϕ \phi ϕ 的过程也是一个贝叶斯过程(词语属于主题的贝叶斯 )。
- 然后第三层是根据主题 z z z 以及词分布 β \beta β 得到主题和单词的一个映射 w w w。
可以用下图表示LDA模型生成文档的过程(K个主题,Nm个单词,M篇文档):

对比一下PLSA,可以看出PLSA的主题分布和词分布都是唯一确定的。但是,在LDA中,主题分布和词分布是不确定的,LDA的作者们采用的是贝叶斯派的思想,认为它们应该服从一个分布,主题分布和词分布都是多项式分布,因为多项式分布和狄利克雷分布是共轭结构,在LDA中主题分布和词分布使用了Dirichlet分布作为它们的共轭先验分布。
使用第三方的lda库实现LDA模型对文档主题的预测:
import numpy as np
import matplotlib.pyplot as plt
import matplotlib as mpl
import lda.datasets # 使用第三方的lda库,安装方式: pip install lda
from pprint import pprint
# 加载数据
X = lda.datasets.load_reuters() # shape: (395, 4258),和x的列数一样
vocab = lda.datasets.load_reuters_vocab() # len(vocab): 4258
titles = lda.datasets.load_reuters_titles() # len(titles): 395,和x的行数一样
# 模型训练
print ('LDA start ----')
topic_num = 20
model = lda.LDA(n_topics=topic_num, n_iter=500, random_state=1)
model.fit(X)
# 获取模型的主题词
topic_word = model.topic_word_ #主题和词
print("shape: {}".format(topic_word.shape)) # shape: (20, 4258),20个主题和4258个单词的关系
for n in range(5):
# topic_word[n, :]是每个主题和每个单词的相关程度,加起来和为1
sum_pr = sum(topic_word[n, :])
print("topic: {} sum: {}".format(n, sum_pr))
#每个主题中的前7个单词
n = 7
for i, topic_dist in enumerate(topic_word):
topic_words = np.array(vocab)[np.argsort(topic_dist)][:-(n + 1):-1]
print('*Topic {}\n- {}'.format(i, ' '.join(topic_words)))
###计算输入前10篇文字最可能的topic
doc_topic = model.doc_topic_ #文档和主题
print("shape: {}".format(doc_topic.shape)) # shape: (395, 20)
for i in range(10):
topic_most_pr = doc_topic[i].argmax()
print(u"文档: {} 主题: {} value: {}".format(i, topic_most_pr, doc_topic[i][topic_most_pr]))
还可以绘制主题单词和文档之间的关系:
#coding:utf-8
plt.rcParams['font.sans-serif'] = ['Arial Unicode MS']
#计算每个主题中单词权重分布情况:
plt.figure(figsize=(8, 9))
# f, ax = plt.subplots(5, 1, sharex=True)
for i, k in enumerate([0, 5, 9, 14, 19]):
ax = plt.subplot(5, 1, i+1)
ax.plot(topic_word[k, :], 'r-')
ax.set_xlim(-50, 4350) # [0,4258]
ax.set_ylim(0, 0.08)
ax.set_ylabel(u"概率")
ax.set_title(u"主题 {}".format(k))
plt.xlabel(u"词", fontsize=14)
plt.tight_layout()
plt.suptitle(u'主题的词分布', fontsize=18)
plt.subplots_adjust(top=0.9)
plt.show()
# Document - Topic
plt.figure(figsize=(8, 9))
for i, k in enumerate([1, 3, 4, 8, 9]):
ax = plt.subplot(5, 1, i+1)
ax.stem(doc_topic[k, :], linefmt='g-', markerfmt='ro')
ax.set_xlim(-1, topic_num+1)
ax.set_ylim(0, 1)
ax.set_ylabel(u"概率")
ax.set_title(u"文档 {}".format(k))
plt.xlabel(u"主题", fontsize=14)
plt.suptitle(u'文档的主题分布', fontsize=18)
plt.tight_layout()
plt.subplots_adjust(top=0.9)
plt.show()


此外也可以用sklearn实现:
参考:
一文详解LDA主题模型





 本文深入探讨了LDA(Latent Dirichlet Allocation)主题模型的原理与应用,包括其生成过程、与pLSA模型的对比,以及如何使用Python的lda库进行文档主题预测。
本文深入探讨了LDA(Latent Dirichlet Allocation)主题模型的原理与应用,包括其生成过程、与pLSA模型的对比,以及如何使用Python的lda库进行文档主题预测。
















 1460
1460

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








