传统神经网络

目录

1. 神经网络起源：线性回归

应用场景

一个线性回归问题

梯度下降：参数更新 m:=m-ηΔm

梯度下降法总结

线性回归

线性回归局限

非线性激励

常用的非线性激励函数

tahn

ReLU

神经元－神经网络

神经网络构建

神经网络的“配件”

损失函数

学习率 Learning rate

过拟合---应对

---

1. 神经网络起源：线性回归

线性回归：线性关系来描述输入到输出的映射关系

应用场景

一个线性回归问题

目标方程：y=ax1+bx2+cx3+d 参数：m=[a,b,c,d]，

数据：[(x1,1,x2,1,x3,1), (x1,2,x2,2,x3,2), …(x1,n,x2,n,x3,n)]

[y1,y2…..yn]

预测：ŷt＝ax1,t+bx2,t+cx3,t+d

目标： minimize (ŷt -yt)，使得预测的y值和真实y值越小越好。

优化方法(优化目标)

模型参数：当前m0 =[a0,b0,c0,d0]，每一步Δm? 参数：m=[a,b,c,d]

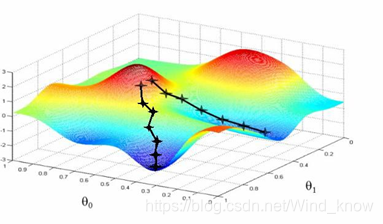
山坡高度：Loss ，将预测值和真实值之间的差距理解为山坡高度。地面位置：参数(abcd参数值)。

山坡最低点：Loss minimal

最低点位置：目标参数

怎么到达最低点：下坡方向，梯度下降 怎么找方向：高度对地面关系导数

梯度下降：梯度计算

Loss=ax1,t+bx2,t+cx3,t+d－y

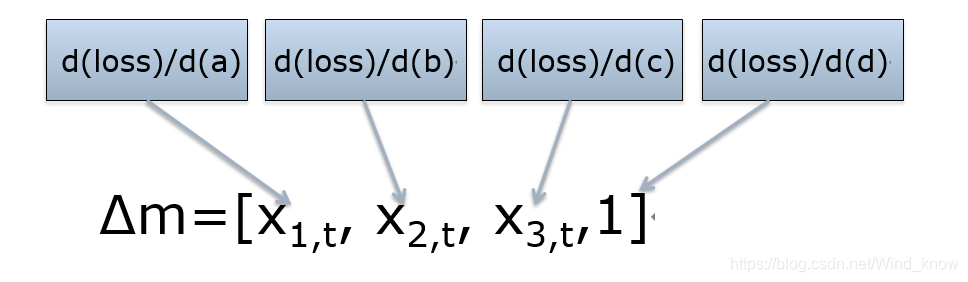
梯度下降：参数更新 m:=m-ηΔm

梯度下降法总结

随机初始化参数。开启循环：t＝0，1，2。带入数据求出结果ŷt，与真值比较得到loss＝y－ŷt，对各个变量求导得到Δm 更新变量m如果loss足够小或t循环结束，停止。

线性回归

输出+

多目标学习，通过合并多个任务loss，一般能够产生比单个模型更好的效果。

线性回归局限

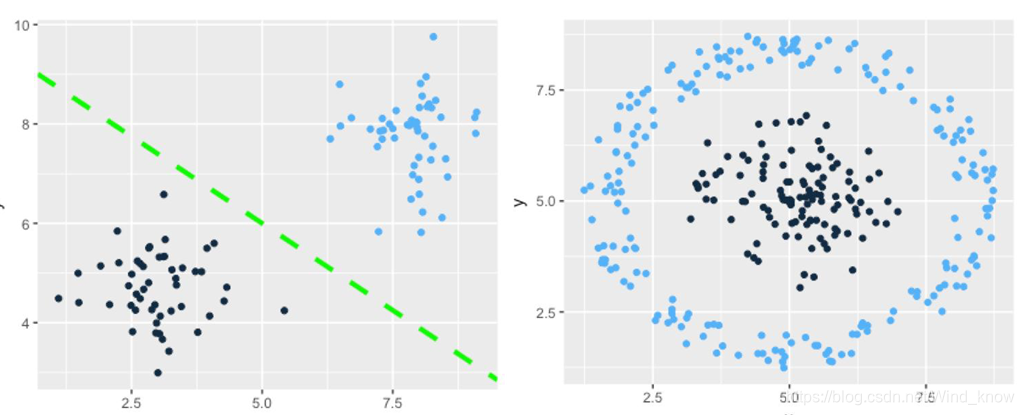
从图上可以看出线性回归能够清楚的描述分割线性分布的数据，对非线性分布的数据描述较弱。

非线性激励

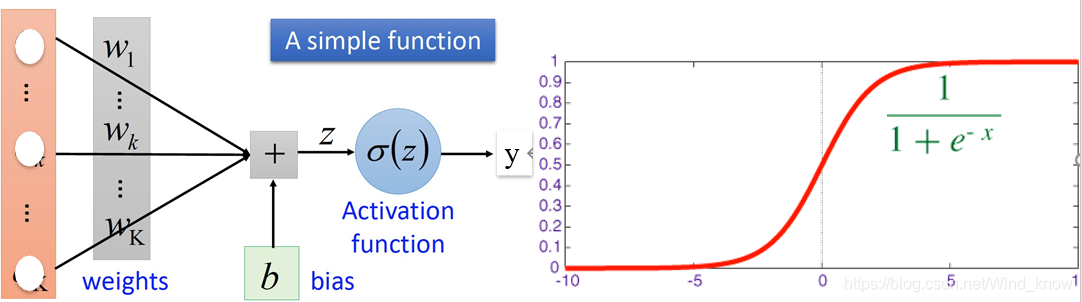
考量标准:1.正向对输入的调整2.反向梯度损失。

常用的非线性激励函数

 

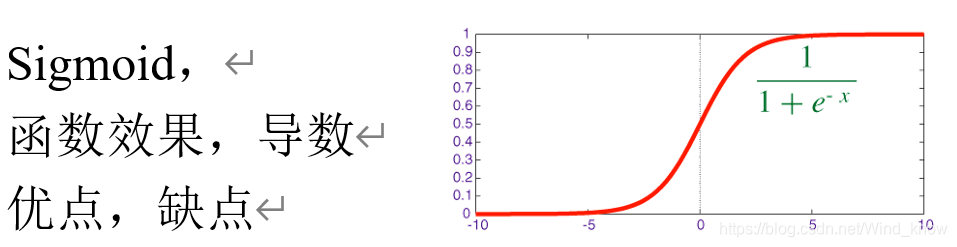
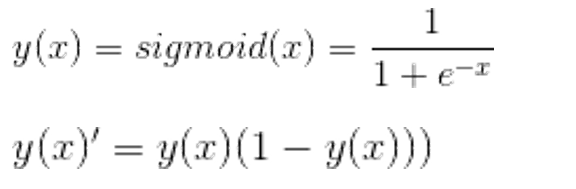
将输入数据映射到[0,1],梯度下降非常明显，至少减少75%。

常用的非线性激励函数

tahn

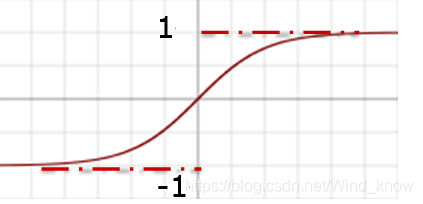
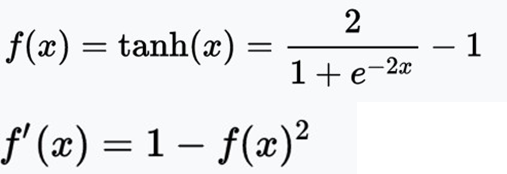
将输入数据映射到［－1，1］，梯度损失明显。

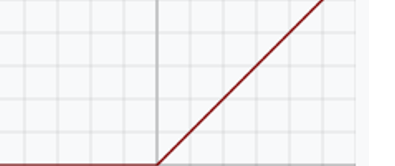
ReLU

函数效果，导数，优点，缺点。

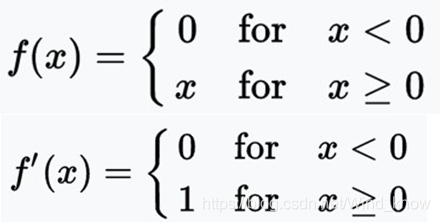
神经元－神经网络

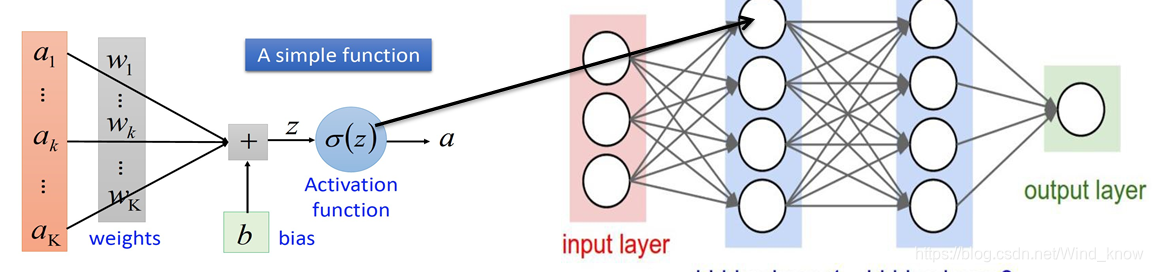
神经网络构建

神经元的“并联”和“串联”，从第一层神经网络到最终输出，每一个神经元的数值由前一层神经元数值，神经元并联：宽度

参数W，b以及激励函数共同决定第n+1层第k个神经元的方程可由公式表示为：

 

 

在这里，m表示第n层神经网络的宽度，n为当前神经网络的深度。

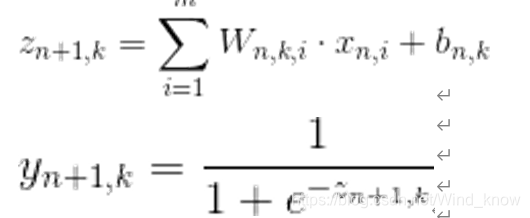
神经网络求导－TensorFlow实现

data = tf.placeholder(tf.float32) var = tf.Variable(...)
loss = some_function_of(var, data)
var_grad = tf.gradients(loss, [var])


sess = tf.Session()
var_grad_val = sess.run(var_grad, feed_dict={data: ...})

神经网络的“配件”

1.损失函数-Loss

2.影响深度学习性能最重要因素之一。是外部世界对神经网络模型训练的直接指导。

3.合适的损失函数能够确保深度学习模型收敛。

4.设计合适的损失函数是研究工作的主要内容之一。

损失函数

学习率 Learning rate

 

过拟合---应对

 

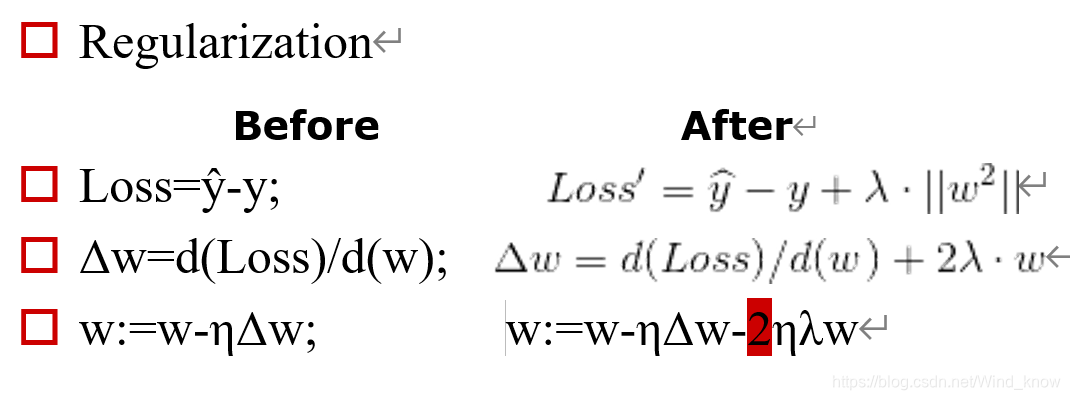
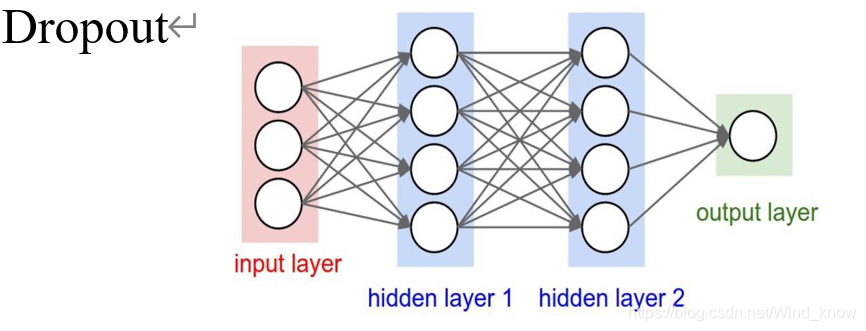
Pooling的本质是降维，Droupout的本质是Regularization。