给定一个排序数组和一个目标值,在数组中找到目标值,并返回其索引。如果目标值不存在于数组中,返回它将会被按顺序插入的位置。
你可以假设数组中无重复元素。
示例 1:
输入: [1,3,5,6], 5
输出: 2
示例 2:
输入: [1,3,5,6], 2
输出: 1
示例 3:
输入: [1,3,5,6], 7
输出: 4
示例 4:
输入: [1,3,5,6], 0
输出: 0
二分查找:
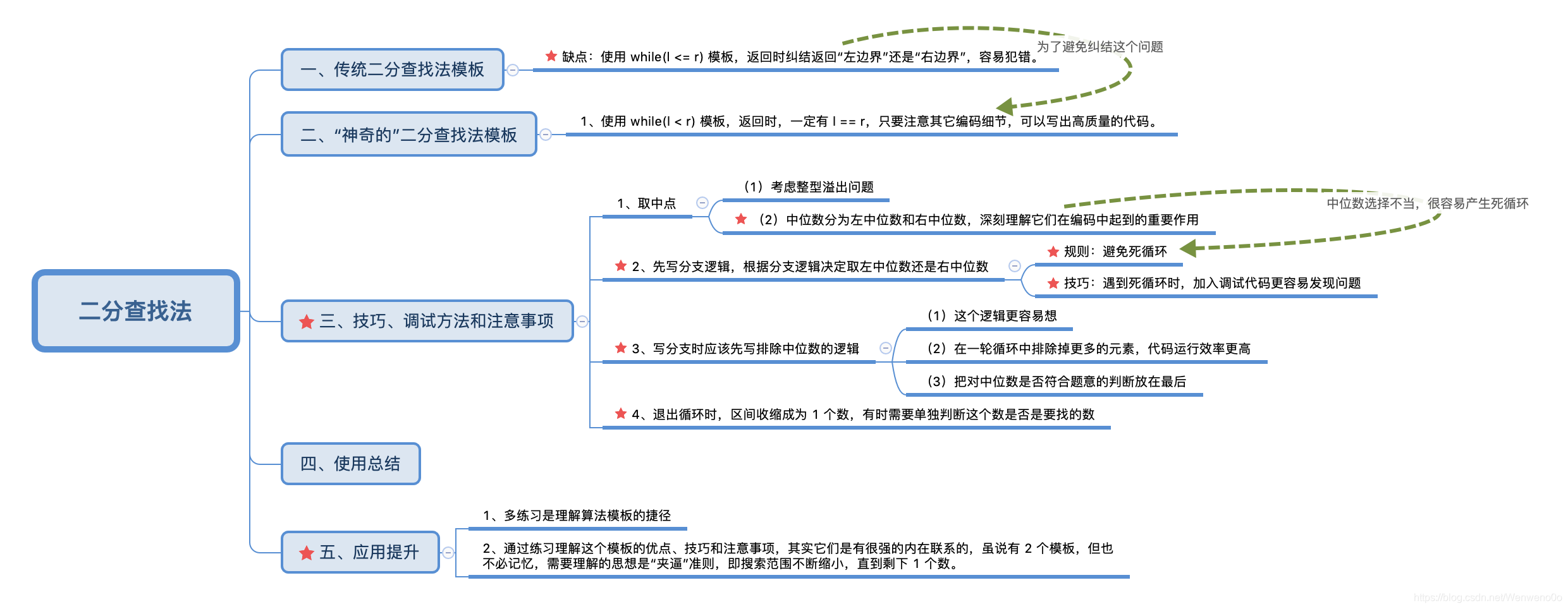
“神奇的”二分查找法模板
二分查找法的思想:二分查找法的思想是“夹逼”,或者说“排除”,而“二分”只是手段。即“通过二分排除了候选区间的一大半的非目标元素”。具体说来,如下:
在每一轮循环中,都可以排除候选区间里将近一半的元素,进而使得候选区间越来越小,直至有限个数(通常为 111 个),而这个数就有可能是我们要找的数(在一些情况下,还需要单独做判断)。
下面我要介绍的“神奇的”二分查找法模板,就把这个思想发挥到了极致。
在一些资料中,你可能看过别人写二分查找法,把循环可以进行的条件写成 while (l < r) ,当时你是不是跟我一样有疑问:“咦?当左右边界一样的时候,那个数岂不是会被漏掉”。但是我要告诉你,这样写在绝大多数情况下是最好的,这也是“神奇的”二分查找法模板好用的一部分。
理由很简单:写 while (l < r) 的时候,退出循环时,左边界等于右边界,因此你不必纠结要返回 l 还是 r ,此时返回 l 或者 r 都是可以的。
二分查找法之所以高效,是因为它利用了数组有序的特点,在每一次的搜索过程中,都可以排除将近一半的数,使得搜索区间越来越小,直到区间成为一个数。回到这一节最开始的疑问:“区间左右边界相等(即收缩成 1 个数)时,这个数是否会漏掉”,解释如下:
1、如果你的业务逻辑保证了你要找的数一定在左边界和右边界所表示的区间里出现,那么可以放心地返回 l 或者 r,而无需再做判断;
2、如果你的业务逻辑不能保证你要找的数一定在左边界和右边界所表示的区间里出现,那么只要在退出循环以后,再针对 nums[l] 或者 nums[r] (此时 nums[l] == nums[r])单独作一次判断,看它是不是你要找的数即可。
阶段总结:
加上了对候选区间是否存在目标元素的思考和判断,写 while (l < r) 这个逻辑就可以避免你对返回左边界还是右边界的讨论。
下面给出这道问题,使用 while (l < r) 模板写法的参考代码。
参考代码:(Java)
class Solution
{
public int searchInsert(int[] nums, int target)
{
int len = nums.length;
if (len == 0)
{
return 0;
}
if (target > nums[len - 1])
{
return len;
}
int left = 0;
int right = len - 1;
while (left < right)
{
int mid = left + (right - left) / 2;
if (nums[mid] < target)
{
left = mid + 1;
}
else
{
right = mid;
}
}
return right;
}
}
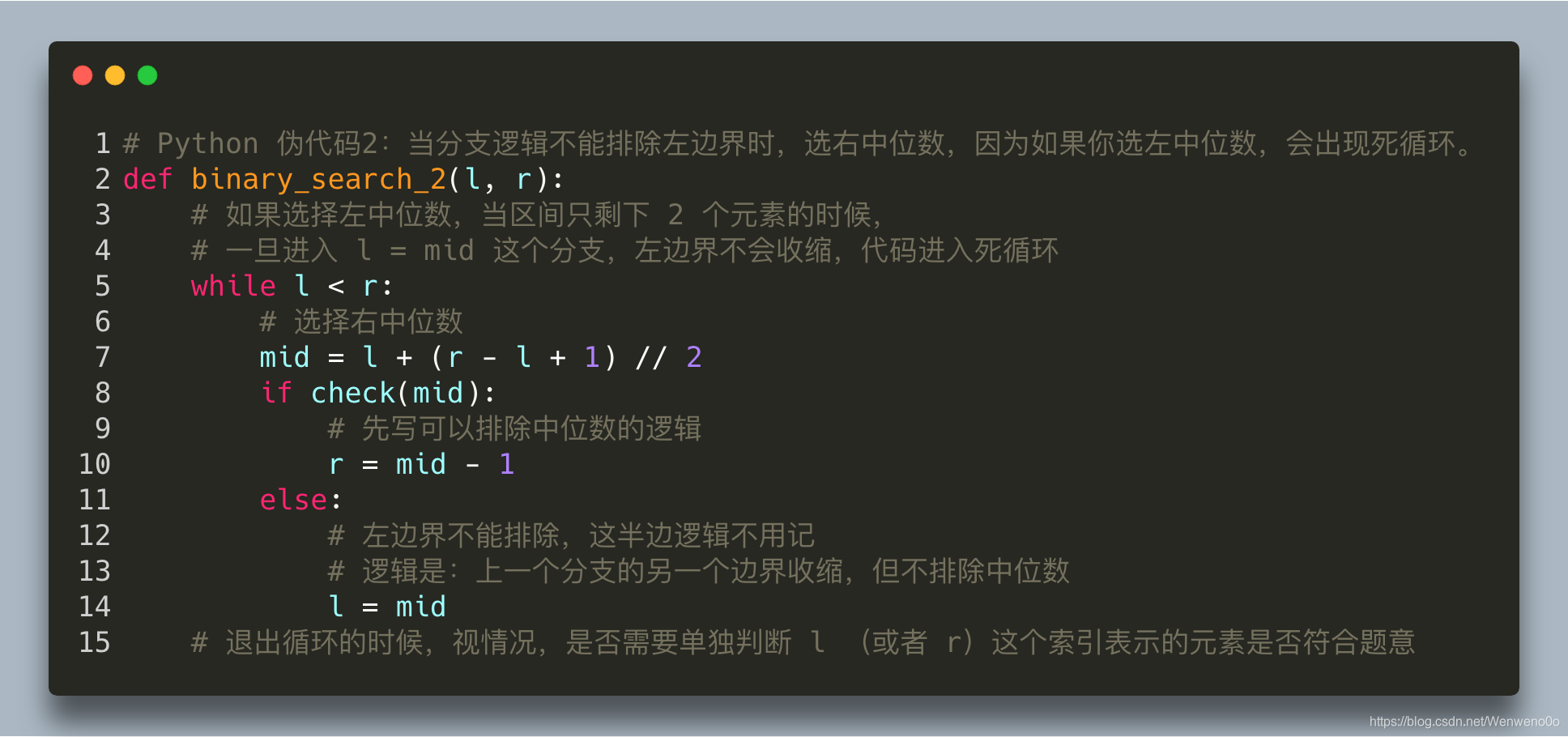
Python
class Solution:
def searchInsert(self, nums, target):
# 返回大于等于 target 的索引,有可能是最后一个
size = len(nums)
if size == 0:
return 0
l = 0
# 如果 target 比 nums里所有的数都大,则最后一个数的索引 + 1 就是候选值,因此,右边界应该是数组的长度
r = size
# 二分的逻辑一定要写对,否则会出现死循环或者数组下标越界
while l < r:
mid = l + (r - l) // 2
if nums[mid] < target:
l = mid + 1
else:
r = mid
return l
最后上逻辑:

























 982
982

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








