决策树和其中划分选择的学习和源码理解

决策树

决策树是基于树结构进行决策的，这是人类在面临决策问题时一种很自然的处理机制。以二分类为例，我们希望从给定训练数据集中学得一个模型用于对新的样例进行分类。

决策树是一种直观的分而治之的策略
决策树包含一个根结点，若干个内部结点和若干个叶结点。
叶结点：对应于决策结果
其他结点：对应于一个属性测试
每个结点包含的样本集合根据属性测试的结果划分到子结点中，根结点包含样本全集，从根结点到每个叶结点的路径对应了一个判定测试序列。
决策树的目的是为了产生一颗泛化能力强的决策树。

决策树的基本流程我就不说了，想了解的同学可以自己查看一下。
决策树学习的关键是如何选择最优的划分属性。我们希望决策树的分支节点所包含的样本尽可能属于同一类别。即纯度越来越高

信息量

显而易见事件B的信息量比事件A的信息量要大。究其原因，是因为事件A发生的概率很大，事件B发生的概率很小。所以当越不可能的事件发生了，我们获取到的信息量就越大。越可能发生的事件发生了，我们获取到的信息量就越小。那么信息量应该和事件发生的概率有关。

假设X是一个离散型随机变量，其取值集合为χ,概率分布函数p(x)=Pr(X=x),x∈χp(x)=Pr(X=x),x∈χ,则定义事件X=x0X=x0的信息量为：

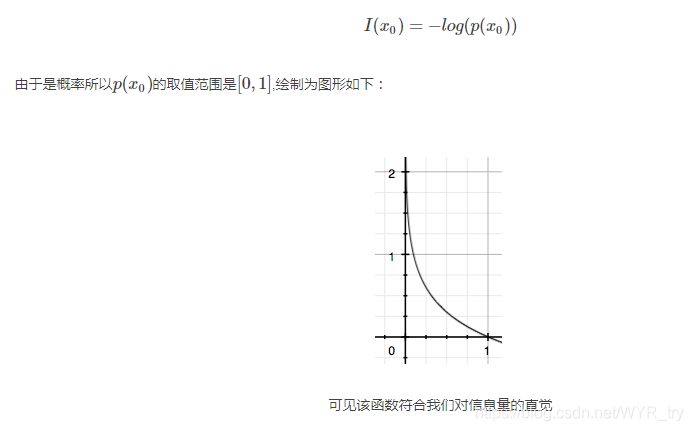
熵

熵的定义就是所有信息量的期望。即每一种可能性乘以它们发生的概率的总和。
公式表示为：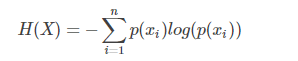

顺带的提一下交叉熵和相对熵：

相对熵：

相对熵又称KL散度,如果我们对于同一个随机变量 x 有两个单独的概率分布 P(x) 和 Q(x)，我们可以使用 KL 散度（Kullback-Leibler (KL) divergence）来衡量这两个分布的差异
即如果用P来描述目标问题，而不是用Q来描述目标问题，得到的信息增量。

在机器学习中，P往往用来表示样本的真实分布，比如[1,0,0]表示当前样本属于第一类。Q用来表示模型所预测的分布，比如[0.7,0.2,0.1]
直观的理解就是如果用P来描述样本，那么就非常完美。而用Q来描述样本，虽然可以大致描述，但是不是那么的完美，信息量不足，需要额外的一些“信息增量”才能达到和P一样完美的描述。如果我们的Q通过反复训练，也能完美的描述样本，那么就不再需要额外的“信息增量”，Q等价于P。

KL散度的计算公式：

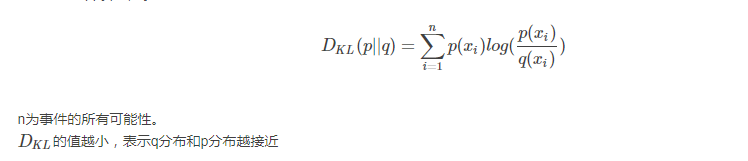
交叉熵：

对相对熵公式进行变形：

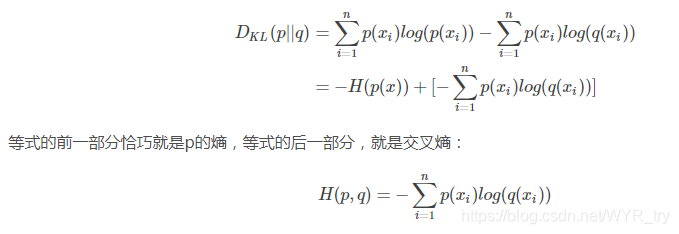
在机器学习中，我们需要评估label和predicts之间的差距，使用KL散度刚刚好，即DKL(y||y^)DKL(y||y)，由于KL散度中的前一部分−H(y)−H(y)不变，故在优化过程中，只需要关注交叉熵就可以了。所以一般在机器学习中直接用用交叉熵做loss，评估模型。

信息增益

信息熵 是度量样本集合纯度最常用的一种指标。假定当前样本集合D中第K类样本所占比例为Pk（k=1,2,3,…y）
Ent(D)=-sum(Pk log2Pk)
Ent(D)值越小，则D的纯度越高。
信息增益的公式为：Gain（D，a）=Ent(a)-sum(|Dv|/|D| * Ent(Dv))
ID3算法就是以此来选择划分的属性

增益率

从信息增益的公式可以看到若D越大，则会导致Gain（D,a）越大，信息增益准则对可取数目较多的属性有所偏好，为了解决这个问题，提出了增益率。
增益率为 Gain_ratio(D,a)=Gain(D,a)/IV(a);
IV(a)=-sum(|Dv|/|D| *l og2(Dv/D))
IV(a)是属性a的固定值，若属性值a取值越多，则IV（a）越大，则增益率会变小。
一定程度上平衡了信息增益准则中这个不利的影响。
C4.5决策树就是使用的增益率来划分。

基尼指数

基尼指用来衡量数据集D的纯度，公式如下：
Gini(D)=sum(PkPk’)=1-sum(PkPk)
直观来说基尼指数反映了从数据集D中随机抽取两个样本，其类别标记不一致的概率。
因此基尼指数越小，数据集纯度愈高。
基尼指数定义为：Gini_index(D,a)=sum(|Dv|/|D| *Gini(D))
我们在候选属性集合A中，选择使得划分后基尼指数最小的属性作为划分属性。

总结

后面还有用了处理过拟合的剪枝处理和连续值与缺省值处理，具体在源码中去阅读理解。

源码