66-插入排序

目录

1.直接插入排序

2.折半插入排序

3.在数组arr[l...r]上使用插入排序

---

类似打扑克牌，整理牌的时候，都是把乱的牌向已经码好的牌中插入——天然的插入排序。

1.直接插入排序

每次选择无序区间的第一个元素，插入到有序区间的合适位置，不断重复此流程，直到整个数组有序。整个区间被分为有序区间[0, i)和无序区间[i, n)。

 /**
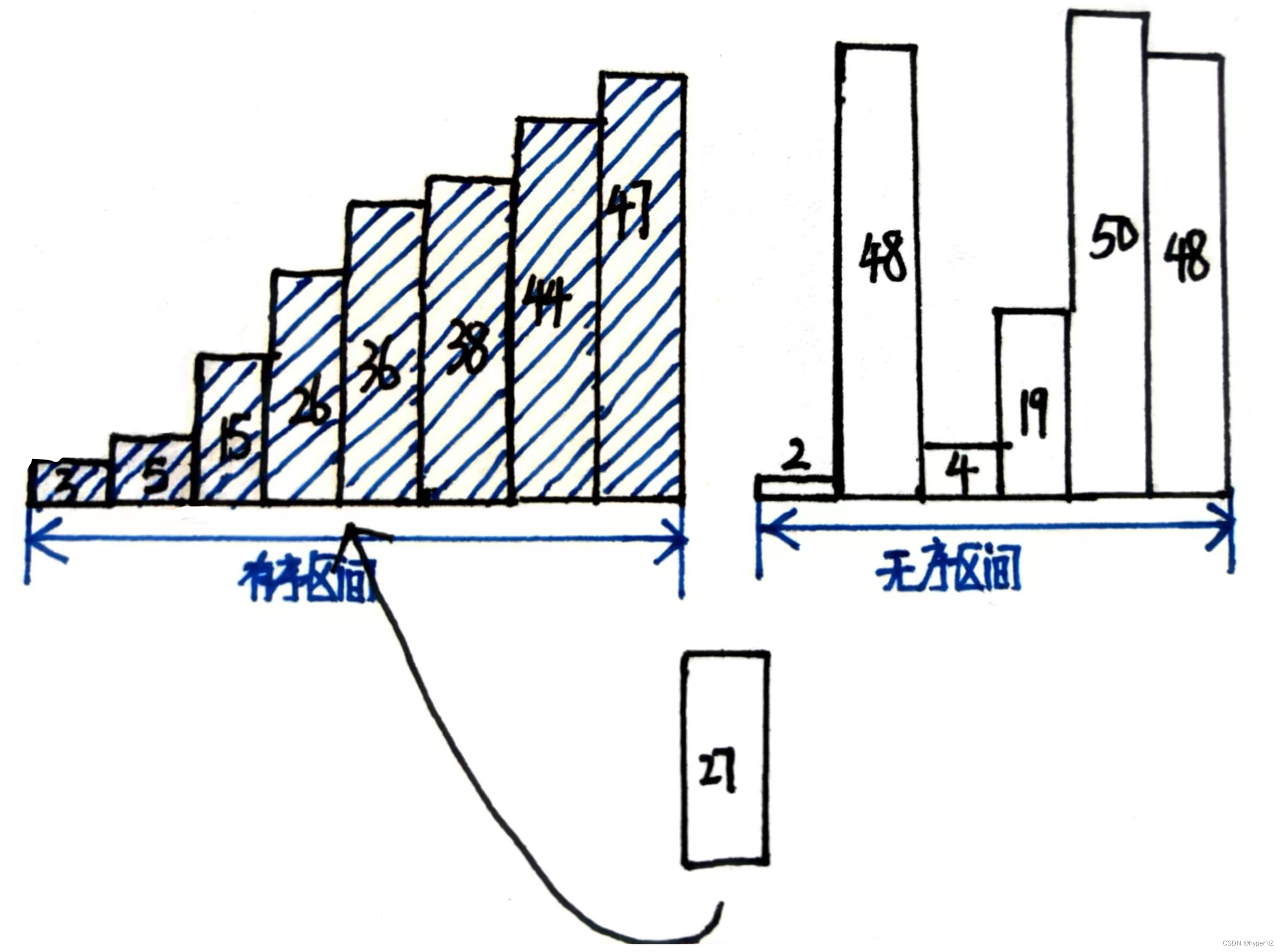
  * 直接插入排序 稳定的
  * 每次选择无序区间的第一个元素，插入到有序区间的合适位置
  * @param arr
  */
public static void insertionSortBase(int[] arr) {
    //有序区间[0,i) [0,1)
    //默认第一个元素就是有序
    for (int i = 1; i < arr.length; i++) {
        //每次选择无序区间的第一个元素，插入到有序区间的合适位置
        //无序区间[i, n)
        for (int j = i; j > 0 && arr[j] < arr[j - 1]; j--) {
            swap(arr, j, j-1);
            //arr[j] > arr[j - 1]此时循环直接终止
            //arr[j - 1]已经是有序区间元素，大于前面的所有值
        }
    }
}

稳定性：稳定。

arr[j] > arr[j - 1]循环就终止了，因此相等元素排序前和排序后的次序不会发生变化。

性能：

时间复杂度：n * 1 + (n - 1) * 2 + (n - 2) * 3 + ... + 2 * (n - 1) + 1 * n => O(n ^ 2)

插入排序和选择排序最大的不同在于：若arr[j] >= arr[j - 1]，循环可以直接终止，arr[j - 1]已经是有序区间元素。

插入排序在小数据规模上，在近乎有序的数组中，性能非常好。经常作为高级排序算法的优化手段。

2.折半插入排序

在有序区间选择数据应该插入的位置时，因为区间的有序性，可以利用折半查找（二分查找）的思想快速定位插入的位置。

/**
 * 折半插入排序
 * @param arr
 */
public static void insertionSortBS(int[] arr) {
    for (int i = 1; i < arr.length; i++) {
        //无序区间第一个值
        int val = arr[i];
        //有序区间[0,i)
        int low = 0;
        int high = i;
        while(low < high) {
            int mid = (low + high) >> 1;
            //将相等的值放在左半区间，保证稳定性
            if(val >= arr[mid]) {
                low = mid + 1;
            }else{
                //右区间取不到，不用 -1
                high = mid;
            }
        }
        //数据搬移
        for (int j = i; j > low; j--) {
            arr[j] = arr[j - 1];
        }
        //low就是元素插入位置
        arr[low] = val;
    }
}

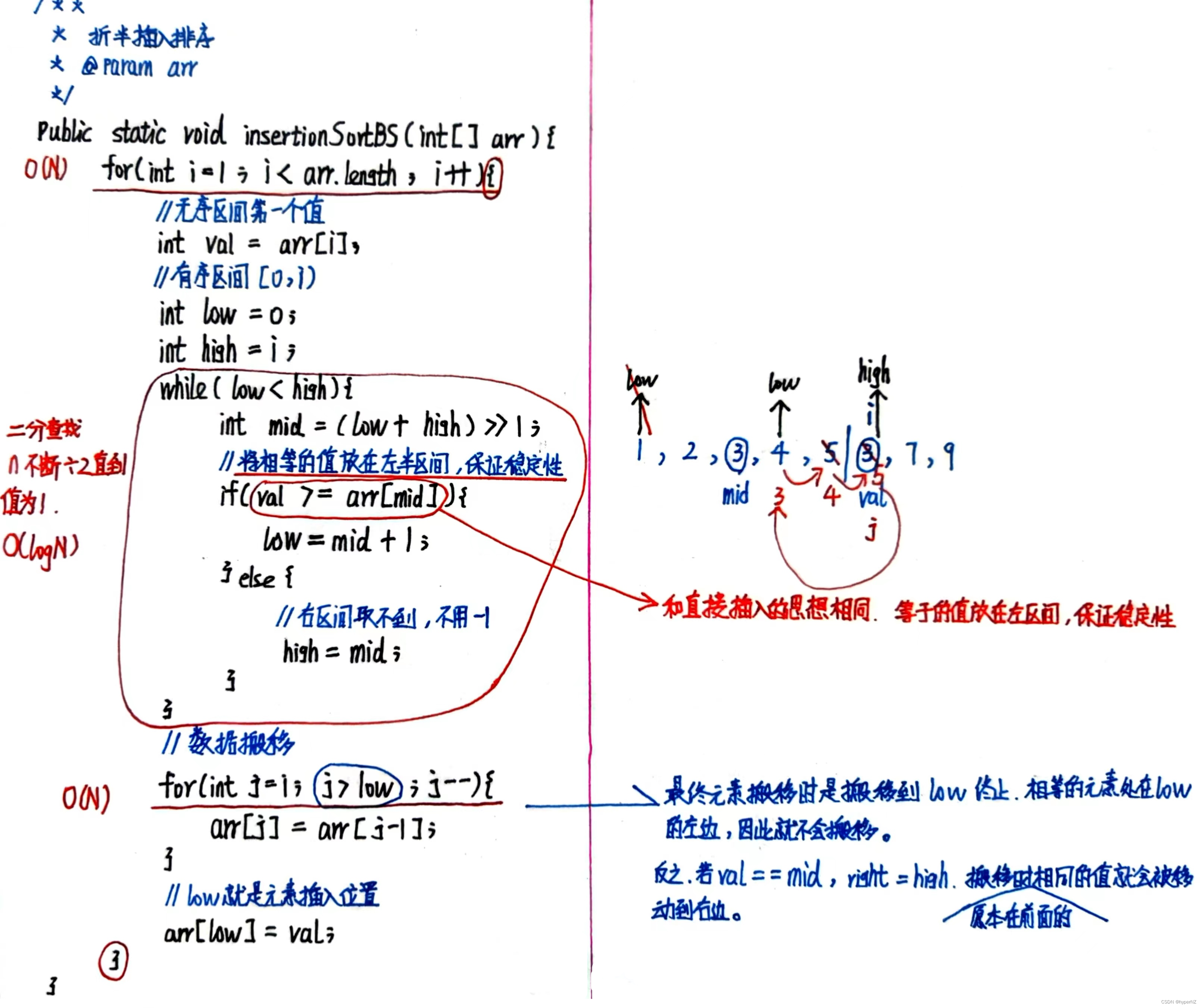
稳定性：稳定。

时间复杂度：n * logn + n * (1...n) => O(N ^ 2)

折半插入排序（一个个比较交换，O(logn)）比直接插入排序（找到插入位置后元素的搬移，O(n)）主要快在查找（有序区间查找）上。

搬移次数 == 交换次数（因为最终插入位置是一样的）。

3.在数组arr[l...r]上使用插入排序

/**
 * 在数组arr[l...r]上使用插入排序
 * @param arr
 * @param l
 * @param r
 */
private static void insertBase(int[] arr, int l, int r) {
    //有序的区间[l...i]
    //无序的区间[i...r]
    for (int i = l + 1; i <= r; i++) {
        for (int j = i; j > l && arr[j] < arr[j - 1]; j--) {
            swap(arr, j, j - 1);
        }
    }
}