栈是一种特殊线性表，遵循后进先出(LIFO)原则，常用于函数调用、浏览器返回、编辑器撤销等场景。核心操作包括push(入栈)、pop(出栈)和peek(查看栈顶元素)。栈可以基于数组或链表实现，提供了动态扩容和获取栈中元素数量的方法。
目录
1.概念
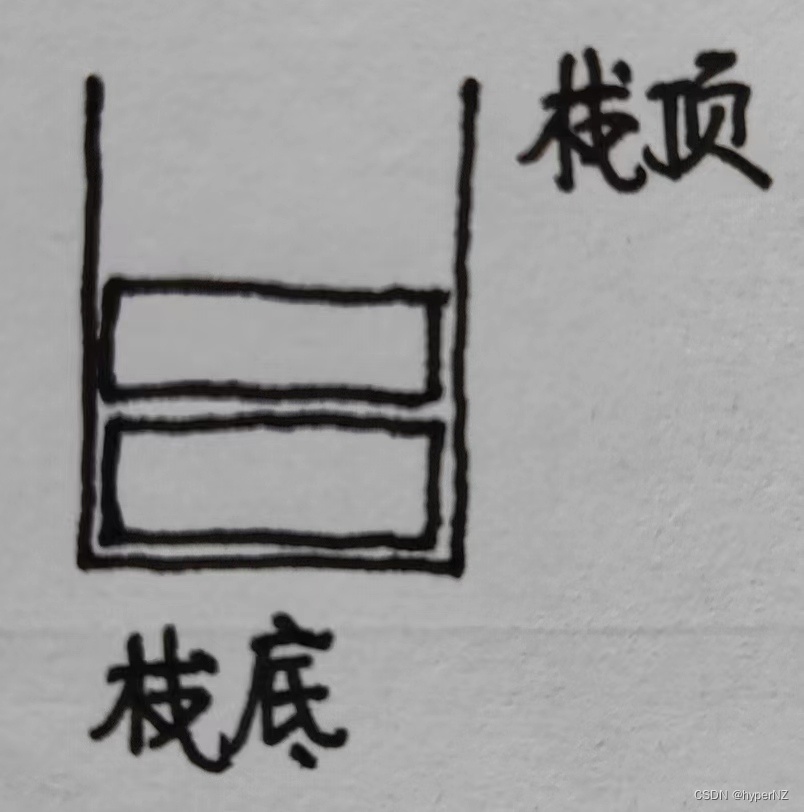
一种特殊的线性表，只允许在固定的一端进行插入和删除元素操作。
进行数据插入和删除的一端叫栈顶，另一端叫栈底。
栈中数据数据元素遵守后进先出LIFO原则。
- 压栈/进栈/入栈：栈的插入操作，入数据在栈顶。
- 出栈：栈的删除操作，出数据在栈顶。
2.应用
①函数调用栈
②浏览器的返回
③编辑器的撤销ctrl + Z
④编辑器的括号匹配
⑤算术运算的符号优先级匹配
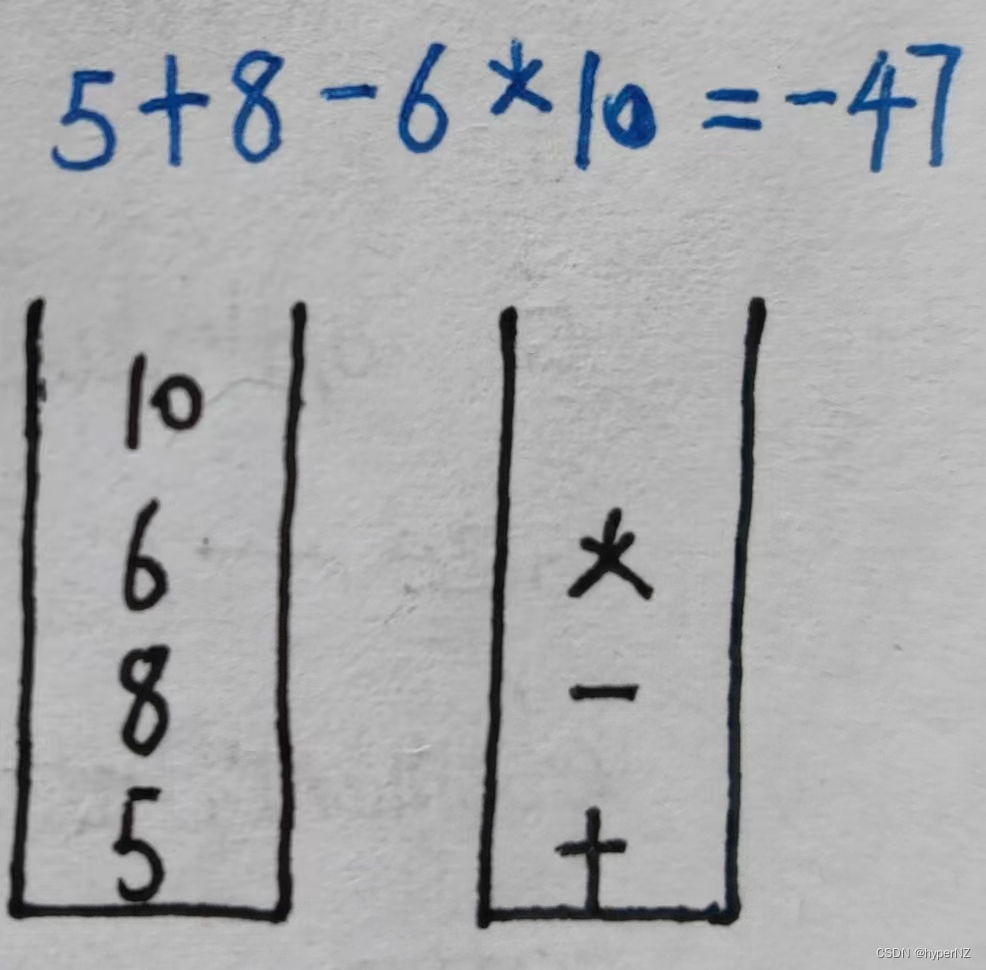
⑥箱子
3.核心操作
①pop()：移除栈顶元素（出栈）
②peek()：查看栈顶元素但不删除
③push()：向栈中添加元素（入栈）
4.分类
栈的底层实现有2种：
①基于数组的实现：顺序栈（物理相邻）（更简单）
②基于链表的实现：链式栈（逻辑相邻）（头尾皆可）
5.方法实现
public class Stack <E> { //E泛型，Stack可以支持所有数据类型，不光是整型
//泛型数组
private E[] elementData;
//当前栈中有效元素的个数
private int size;
//无参构造方法
public Stack() {
elementData = (E[]) new Object[10]; //使用时E有具体类型，一定是Object的子类
//默认size = 0;
}
//有参构造方法
public Stack(int initCap) {
elementData = (E[]) new Object[initCap]; //规定数组初始长度
//默认size = 0;
}
//具体方法实现
//...
}5.1.入栈操作
/**
* 入栈操作
* @param value
*/
public void push(E value) {
//扩容
if(size == elementData.length) {
int oldLength = elementData.length;
int newLength = oldLength << 1;
//将原数组搬移到新数组
elementData = Arrays.copyOf(elementData, newLength);
}
elementData[size++] = value;
//即为 elementData[size] = value;
// size++;
}5.2.出栈操作，返回原先的栈顶元素
/**
* 出栈操作，返回原先的栈顶元素
* @return
*/
public E pop() {
if(getSize() == 0) {
//当前栈为空
throw new NoSuchElementException("栈为空！");
}
E oldValue = elementData[size - 1];
size--;
elementData[size] = null;
return oldValue;
}5.3.查看栈顶元素，不出栈
/**
* 查看栈顶元素，不出栈
* @return
*/
public E peek() {
if(getSize() == 0) {
throw new NoSuchElementException("栈为空！");
}
return elementData[size - 1];
}5.4.获取栈中有效元素个数
/**
* 获取栈中有效元素个数
* @return
*/
public int getSize() {
return size;
}5.5.toString()方法
public String toString() {
StringBuilder sb = new StringBuilder();
sb.append("[");
for (int i = 0; i < size; i++) {
sb.append(elementData[i]);
if(i != size - 1) {
sb.append(",");
}
}
sb.append("] top");
return sb.toString();
}6.总代码实现
import java.util.Arrays;
import java.util.NoSuchElementException;
public class Stack <E> { //E泛型，Stack可以支持所有数据类型，不光是整型
//泛型数组
private E[] elementData;
//当前栈中有效元素的个数
private int size;
//无参构造方法
public Stack() {
elementData = (E[]) new Object[10]; //使用时E有具体类型，一定是Object的子类
//默认size = 0;
}
//有参构造方法
public Stack(int initCap) {
elementData = (E[]) new Object[initCap]; //规定数组初始长度
//默认size = 0;
}
/**
* 入栈操作
* @param value
*/
public void push(E value) {
//扩容
if(size == elementData.length) {
int oldLength = elementData.length;
int newLength = oldLength << 1;
//将原数组搬移到新数组
elementData = Arrays.copyOf(elementData, newLength);
}
elementData[size++] = value;
//即为 elementData[size] = value;
// size++;
}
/**
* 出栈操作，返回原先的栈顶元素
* @return
*/
public E pop() {
if(getSize() == 0) {
//当前栈为空
throw new NoSuchElementException("栈为空！");
}
E oldValue = elementData[size - 1];
size--;
elementData[size] = null;
return oldValue;
}
/**
* 查看栈顶元素，不出栈
* @return
*/
public E peek() {
if(getSize() == 0) {
throw new NoSuchElementException("栈为空！");
}
return elementData[size - 1];
}
/**
* 获取栈中有效元素个数
* @return
*/
public int getSize() {
return size;
}
public String toString() {
StringBuilder sb = new StringBuilder();
sb.append("[");
for (int i = 0; i < size; i++) {
sb.append(elementData[i]);
if(i != size - 1) {
sb.append(",");
}
}
sb.append("] top");
return sb.toString();
}
}7.测试实现
public class StackTest {
public static void main(String[] args) {
Stack<Integer> stack = new Stack<>();
stack.push(1);
stack.push(3);
stack.push(5);
System.out.println(stack); //[1,3,5] top
System.out.println(stack.peek()); //5
stack.pop();
System.out.println(stack); //[1,3] top
}
}
扫一扫
1872
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
