Python+OpenCv 标定相机参数的实现

最新推荐文章于 2025-09-29 15:12:36 发布

原创

最新推荐文章于 2025-09-29 15:12:36 发布 · 2k 阅读

14 ·

CC 4.0 BY-SA版权

本文详细介绍了利用Python和OpenCV进行相机参数标定的步骤，包括制作标定板、提取世界坐标、张正友标定方法及其原理、相机内参数计算和消除径向畸变。通过实验展示了标定结果，强调了反投影误差在评估标定质量中的作用，并提醒注意标定过程中保持棋盘格平整以减少误差。

文章目录

一、制作标定板

用matlab软件写代码生成了一个棋盘格图在这里插入图片描述

将上图棋盘格图片打印，然后再将打印出的纸固定放到一个平板上，使用同一相机从不同的位置，不同的角度，拍摄标定板的多张照片（10-20张最佳），将照片放到文件夹中：

二、提取标定板的世界坐标

需要注意标定板的大小是标定板在水平和竖直方向上内角点的个数。内角点指的是，标定板上不挨着边界的角点（如图我的实验标定板大小为6×4）。

三、张正友标定相机

（一）原理描述

张正友于1998年在论文："A Flexible New Technique fro Camera Calibration"提出了基于单平面棋盘格的相机标定方法。该方法介于传统的标定方法和自标定方法之间，使用简单实用性强，有以下优点：
1.不需要额外的器材，一张打印的棋盘格即可。
2.标定简单，相机和标定板可以任意放置。
3.标定的精度高。

（二）相机内参数

设 P=(X,Y,Z)P=(X,Y,Z) P=(X,Y,Z)P=(X,Y,Z) 为场景中的一点，进行下面几个步骤：
1.将 P 从世界坐标系通过刚体变换变换到相机坐标系，这个变换过程使用的是相机间的相对位姿，也就是相机的外参数。
2.从相机坐标系，通过透视投影变换到相机的成像平面上的像点p=(x,y)。
3.将像点p从成像坐标系，通过缩放和平移变换到像素坐标系上点p=(μ,ν)。
我们就可以将场景中的三维点转换成图像中的二维点了。上述的变换步骤转换成具体的数学形式：
在这里插入图片描述
将矩阵K视为相机的内参数

（三）单应矩阵

在张氏标定法中，用于标定的棋盘格是三维场景中的一个平面 Π；其在成像平面的像是另一个平面 π，由于棋盘格的角点是已知的，我们可以通过角点提取算法获得图像中的角点，知道了两个平面的对应点的坐标，就可以求解得到两个平面的单应矩阵。
通过上面的相机模型有：
在这里插入图片描述
其中p是像点坐标，P是标定的棋盘坐标。这样就可以得到下面的等式：

H 表示的是成像平面和标定棋盘平面之间的单应矩阵。通过对应的点对解得H后，则可以通过上面的等式得到相机的内参数 K，以及外参旋转矩阵R 和平移向量 t。
将一个平面映射到另一个平面，将棋盘格所在的平面映射到相机的成像平面，可以获得公式：
在这里插入图片描述
其中p为棋盘格所成像的像点坐标，P 棋盘格角点在世界坐标系的坐标。
设棋盘格所在的平面为世界坐标系中Z=0的平面，则根据相机模型：

根据单应性，将公式进行整合，可以得到单应矩阵H和相机矩阵（包含内参和外参）的相等：
在这里插入图片描述
这样就能通过单应矩阵H来约束相机的内参和外参，单应矩阵H可以通过棋盘平和成像平面上对应的点计算出来。

（四）内参约束条件

通过平面间的单应，可以把H矩阵(3*3)写成3个列向量形式，我们把H矩阵写成：
在这里插入图片描述
r1和r2标准正交，结合上面可以获得两个内参的约束等式：

（五）求解内参数

通过一幅标定板的图像可以的得到关于内参数的两个等式，令通过一幅标定板的图像可以的得到关于内参数的两个等式，令
在这里插入图片描述
可知B矩阵是个对称矩阵，所以可以写成一个6维向量形式

我们把HH HH矩阵的列向量形式为： hi=[hi1,hi2,hi3]T hi=[hi1,hi2,hi3]T \ h_i = [h_{i1},h_{i2},h_{i3}]^T hi=[hi1,hi2,hi3]T

整合公式：在这里插入图片描述
再结合上面求出的内参的约束条件，可得到矩阵：

若有n幅图像，则 Vb=0
其中，V是一个2n×6的矩阵，b是一个6维向量，所以:
当n≥3，可以得到b的唯一解;
当n=2，则可以假设扭曲参数γ=0作为额外的约束条件
当n=1，则值能计算两个相机的内参数
对于方程Vb=0可以使用SVD求得其最小二乘解。对 V^T进行SVD分解，其最小特征值对应的特征向量就是Vb=0的最小二乘解，从而求得矩阵B。
可以得到相机的各个内参数：
在这里插入图片描述

（六）最大似然估计

由于上面估计获得的解可能存在高斯噪声，所以使用最大似然估计进行优化。假设同一相机从n个不同的角度的得到了n幅标定板的图像，每幅图像上有m个像点。 M_{ij}表示第i幅图像上第j个像点对应的标定板上的三维点，则
在这里插入图片描述
m^(K,Ri,ti,Mij)表示M_{ij}的像点。其中，Ri,ti表示第i幅图像对应相机的旋转矩阵和平移向量，K是相机的内参数。则像点 m_{ij}的概率密度函数是

构造似然函数:

让L取得最大值，即让下面式子最小:
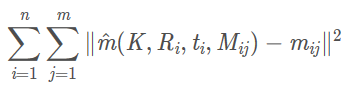
在这里插入图片描述

（七）消除径向畸变

为了取得好的成像效果，通常要在相机的镜头前添加透镜。在相机成像的过程中，透镜会对光线的传播产生影响，从而影响相机的成像效果，产生畸变。
透镜自身的形状对才光线的传播产生影响，形成的畸变称为径向畸变。在小孔模型中，一条指向在成像平面上的像仍然是直线。但是在实际拍摄的过程中，由于透镜的存在，往往将一条直线投影成了曲线，越靠近图像的边缘，这种现象越明显。透镜往往是中心对称的，使得这种不规则的畸变通常是径向对称的。主要有两大类：桶形畸变和枕形畸变。